9.13日模考总结

本周进行了标准OI普及组模考测试

得分情况

题目名称	做法	预计得分	实际得分
质数差列	模拟、素数筛	100	100
旅行	二分答案	100	40
小桃的物质阵列	思维 + 模拟（双指针）	0	0
幽邃魔窟	01背包变形	20	60

感觉第二题有点可惜，忘了输出 -1 和数据范围了
第四题也有点可惜，没想到是01背包

做题过程

首先是第一题，非常简单的一道题目，直接欧拉筛、埃氏筛（甚至暴力枚举都可以）筛除素数，统计即可，用时5分钟

接着做第二题，一开始的思路是直接用走的路程 \(\div\) 除去游玩的天数，但是是每一次都向上取整，会出错，于是我就用二分的思路来做，写了一个二分10分钟就给调对了

看到第三题，看了好久没看懂题目第三点要求是什么意思，所以就跳过了

做第四题，当时还想用搜索，但是数据范围过大，所以我就用了一个“贪心”，把这些部落按子民数量降序排序，优先选子民多的

回到第三题，后面读着读着看懂了，但是这3点要求实在太苛刻，我没找到规律，暴力都 WA，所以没拿到分

赛后感想

第一题没什么好说的，直接AC

第二题有些可惜，因为我没有判断-1的情况，而且r的范围设小了，所以才40分

第四题60分，比预估的高，正解是01背包
（其实我当时想到了DP的做法,但是没想到是最简单的01背包，挺可惜的）

题解

T1

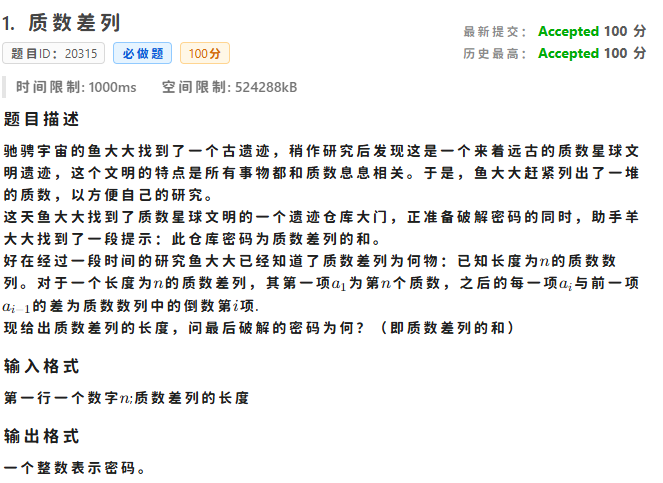
非常简单，首先用任意方法（素数筛、优化的枚举）求出前 \(n\) 个素数，然后用后缀和直接统计答案即可

这里我以欧拉筛举例

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e4 + 10;
const int M = 2e5 + 10;
int n;
bool vis[M];
int a[N];
int cnt;
signed main()
{
    cin >> n;
    for (int i = 2; i <= M && cnt < n; i++)
    {
        if (!vis[i])
        {
            cnt++;
            a[cnt] = i;
        }
        for (int j = 1; j <= cnt && i * a[j] <= M; j++)
        {
            vis[i * a[j]] = true;
            if (i % a[j] == 0)
            {
                break;
            }
        }
    }
    int ans = 0;
    int t = 0;
    for (int i = n; i >= 1; i--)
    {
        t += a[i];
        ans += t;
    }
    cout << ans << endl;
    return 0;
}

T2

我们发现本题有单调性，速度越快时间越少，所以我们就可以使用二分答案来做，用二分枚举速度，看看能不能游玩完所有地点，可以就 \(r = mid\)，否则 \(l = mid + 1\)

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
int n, m;
int a[N], d[N];
inline bool check(int mid)
{
    int day = 0;
    for (int i = 1; i <= n; i++)
    {
        day += ceil((double)a[i] * 1.0 / mid);
        day += d[i];
    }
    return day <= m;
}
signed main()
{
    cin >> n >> m;
    int cnt = 0;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i] >> d[i];
    }
    int l = 1, r = 1e15;
    while (l < r)
    {
        int mid = (l + r) >> 1;
        if (check(mid))
        {
            r = mid;
        }
        else
        {
            l = mid + 1;
        }
    }
    if (r == 1e15)
    {
        cout << -1 << endl;
    }
    else
    {
        cout << r << endl;
    }
    return 0;
}

T3

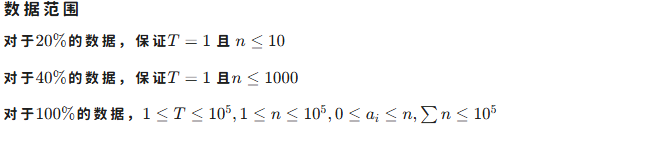
解题思路

（老师上课讲的思路有点晕我换了种方法说）

1. 排序与满足条件的构造
   每个 $ a_i $ 实际上表示了 $ b_i $ 的相对大小以及它与其他元素的关系。由于 $ a_i $ 的值取决于 $ b_i $ 的相对大小，可以通过将元素从小到大排序，然后分两组（正数和负数）进行分配。
   对于排序后的数组，假设按照大小顺序分配正负数（较小的数分配为负，较大的数分配为正），可以满足条件 2 和条件 3。

2. 填充排列细节
   对于每个 $ i $，根据 $ a_i $ 的值，将其设为一个能满足条件的数：
   如果 $ a_i $ 较小，则将其设置为负数。
   如果 $ a_i $ 较大，则将其设置为正数。
   为了满足条件 3，需要确保分配的正负数的个数符合 $ a_i $ 的值。

3. 实现步骤
   将 $ a_i $ 和其对应的索引 $ i $ 绑定，按照 $ a_i $ 的大小进行排序。
   构造 $ b_i $：
   初始化一个数组 $ b $。
   使用两个指针分别处理正数和负数。正数从大到小放置，负数从小到大放置。
   如果可以构造出合法的 $ b_i $，输出 “YES” 并输出排列；否则输出 “NO”。

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
pair<int, int> a[N];
int b[N];
inline bool solve(int n)
{
    sort(a + 1, a + n + 1);
    int l = 1, r = n, cnt = 0;
    for (int i = n; i >= 1; i--)
    {
        if (a[r].first - cnt == i)
        {
            b[a[r].second] = i;
            cnt++;
            r--;
        }
        else if (a[l].first - cnt == 0)
        {
            b[a[l].second] = -i;
            l++;
        }
        else
        {
            return false;
        }
    }
    return true;
}
signed main()
{
    int t;
    cin >> t;
    while (t--)
    {
        int n;
        cin >> n;
        for (int i = 1; i <= n; i++)
        {
            cin >> a[i].first;
            a[i].second = i;
        }
        bool res = solve(n);
        if (res)
        {
            cout << "YES\n";
            for (int i = 1; i <= n; i++)
            {
                cout << b[i] << " ";
            }
            cout << "\n";
        }
        else
        {
            cout << "NO\n";
        }
    }
    return 0;
}

T4

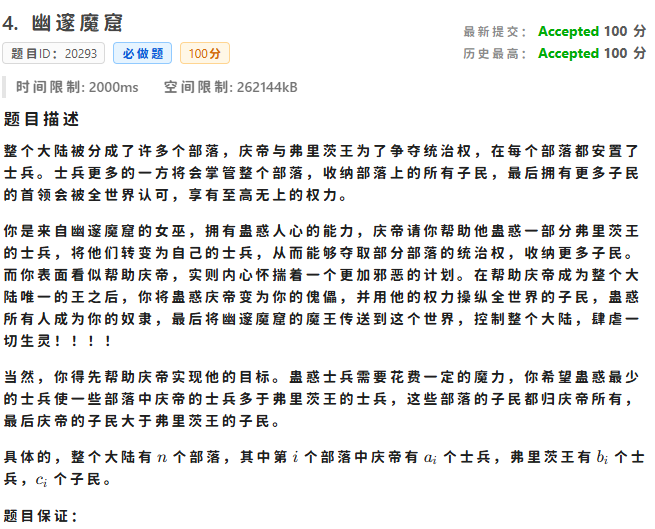
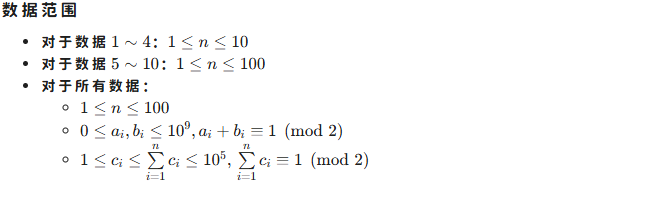
这两个人的名字难打，我们就把庆帝比作中国，弗里茨王比作日本

我们发现，对于每一个部落，如果蛊惑了这里的士兵，那么就代表一定要拿下这里，我们可以看做“选”和“不选”

那么我们发现，对于每一个部落，如果这里是日本的领地，那么拿下他需要的代价为 \((b_i - a_i + 1) \div 2\) （括号里是向上取整的）

所以一个拿下部落的代价为 \(max(0, (b_i - a_i + 1) \div 2)\) ，而我们得到的就是当地的子民数量 \(c_i\)

那么，有了选和不选、代价、价值，就可以01背包辣！

注意，这里我们先把 \(dp\) 全部设为 \(\infty\) ，这里我们如果想要击败日本，那么就得得到一半以上的子民，所以 \(m = (所有子民数量 + 1) \div 2\)

DP的时候要注意，平常我们忽略 \(j < w_i\) （\(W_i\) 是代价）的情况，这个时候，我们不能忽略，因为他减去代价是负数的话，我们就得把他变成0来做

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n;
int a[100005], b[100005], c[100005];
int dp[100005];
int cost[100005];
signed main()
{
    cin >> n;
    int sum = 0;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i] >> b[i] >> c[i];
        sum += c[i];
        cost[i] = max(0LL, (b[i] - a[i] + 1) / 2);
    }
    int m = (sum + 1) / 2;
    memset(dp, 0x3f, sizeof(dp));
    dp[0] = 0;
    for (int i = 1; i <= n; i++)
    {
        for (int j = m; j >= 0; j--)
        {
            int idx = (j >= c[i]) ? (j - c[i]) : 0;
            if (dp[idx] != 0x3f3f3f3f3f3f3f3f)
            {
                dp[j] = min(dp[j], dp[idx] + cost[i]);
            }
        }
    }
    cout << dp[m] << endl;
    return 0;
}