9.6日模考总结

本周进行了标准OI普及组测试

得分情况

题目名称	做法	预计得分	实际得分
A 彩虹豆	map统计	100	100
B 机场代码	模拟	100	100
C 网格和磁铁	dfs搜索	30	30
D 划分区间	数学、找规律	100	100

做题流程

先做第一题，非常简单的一道题，直接用一个 map 统计一下每一种豆子的最小值，求最大值即可，只用了3分钟

接着来到第二题，也是非常简单，看一下字符串 \(S\) 中有没有子序列是 \(T\) （不区分大小写），有就直接输出，还可以考虑一下取两个最后加 X 的情况，用时5分钟

接着第三题，非常搜索，我直接写了一个 dfs ，但是当时我实在想不到怎么剪枝，我还试过记忆化，但是会 WA，所以我直接暴搜，用时10分钟，后续思考了20分钟

最后看到第四题，看懂题意后直接写了一个暴力，思路是分区间的时候枚举 \(j\) 除一除，但是这样思路很乱，第一个样例 RE，我当时还以为是我的代码问题，以为所有样例都会RE，所以一直调，还以为是-1的问题和除以0，但是后来我调不出来随手测了一下样例2，居然没有RE！

我就顺藤摸瓜，顺着那个思路写，调，但是中途我又放弃了，因为错的实在太离谱，第一个样例永远是RE的，但是我在发呆的时候灵感突发，找了一下规律，还别说，真给我找到了！

就是这里的 \(l,r\) ，有的是+1，有的是 ×2，还有的是 +2，所以我就发现了规律：

• 如果当前 \(l_i\) 是0，\(r_i\)就可以是任何一个小于输入的\(r\)的数，前提是这个数2的幂次
• 如果当前 \(l_i\) 是2的幂次，可以×2
• 如果是2的倍数可以+2
• 否则就+1

后面我又根据错误样例调了一会儿，得出一下规律：

• 如果当前 \(l_i\) 是0，\(r_i\)就可以是任何一个小于输入的\(r\)的数，前提是这个数2的幂次
• 如果当前 \(l_i\) 是2的倍数，我们找一个数 \(x\) ，当且仅当\(x\)是\(l_i\)的所有质因数2相乘的积

然后样例全部都过了，直接交卷

赛后心得

发现前两题A了，第三题TLE30，第四题A了，全都在我意料之中，因为我算过T3的时间复杂度，感觉前三题拿到了应该拿到的分，第四题A的漂亮！这次模考确实简单

题解

T1

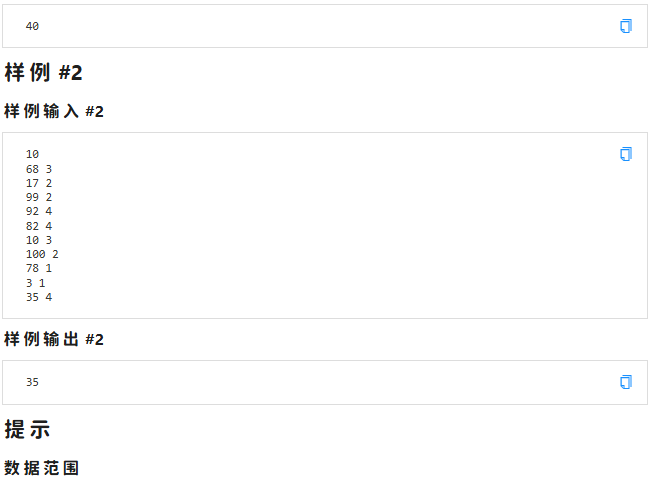
可以用一个 map 统计每一种颜色的豆豆美味度最小值，最后输出 map 里面的最大值即可
code

#include <bits/stdc++.h>
using namespace std;
int n;
int a[200005];
int c[200005];
map<int, int> mp;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        cin >> c[i];
        if (!mp[c[i]])
        {
            mp[c[i]] = 1e10;
        }
        mp[c[i]] = min(mp[c[i]], a[i]);
    }
    int ans = 0;
    for (auto it : mp)
    {
        ans = max(ans, it.second);
    }
    cout << ans << endl;
    return 0;
}

T2

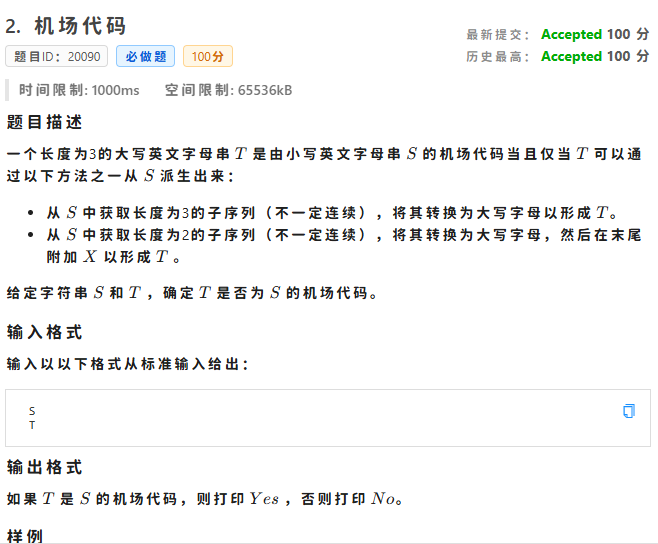
也是非常简单，先判断普通情况，在判断末尾加上 X 的情况即可
code

#include <bits/stdc++.h>
using namespace std;
string s, t;
/// 将小写字母转换为大写字母是-32，大写字母转换为小写字母+32
bool vist[3];
int main()
{
    cin >> s >> t;
    int sum = 0;
    for (int i = 0; i < s.length(); i++)
    {
        if (s[i] - 32 == t[sum])
        {
            vist[sum] = true;
            sum++;
        }
        if (sum == 3) break;
    }
    if (sum == 3) cout << "Yes";
    else if (sum == 2 && t[2] == 'X') cout << "Yes";
    else cout << "No";
    return 0;
}

T3

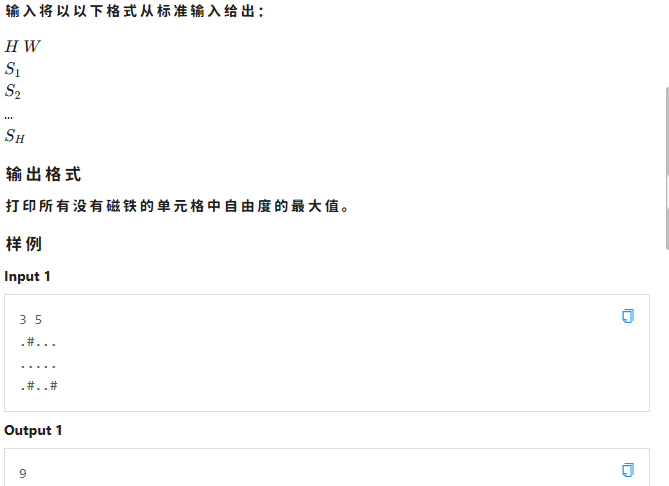
我们如果直接 dfs 暴搜，每次都要 memset 一下子，会超时，我们为了避免这样的情况，可以通过连通分量的思路解决

用染色数组标记连通块，直接求值，其中遇到被磁铁吸住的地方特殊判断一下（化为1），最后输出答案
code

#include <bits/stdc++.h>
#define int long long
using namespace std;
char mp[1010][1010];
int a[1010][1010];
int vis[1010][1010];
int dx[] = {0, 0, -1, 1}, dy[] = {-1, 1, 0, 0};
int ans;
int sum;
int n, m;
void dfs(int x, int y, int cnt)
{
    sum++;
    vis[x][y] = cnt;
    if (a[x][y] == 1)
    {
        return;
    }
    for (int i = 0; i < 4; i++)
    {
        int xx = x + dx[i];
        int yy = y + dy[i];
        if (xx < 1 || xx > n || yy < 1 || yy > m)
        {
            continue;
        }
        if (a[xx][yy] <= 1 && vis[xx][yy] != cnt)
        {
            dfs(xx, yy, cnt);
        }
    }
}
signed main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> mp[i][j];
            if (mp[i][j] == '.')
                a[i][j] = max(a[i][j], 0ll);
            if (mp[i][j] == '#')
            {
                a[i][j] = max(a[i][j], 2ll);
                for (int k = 0; k < 4; k++)
                {
                    int x = i + dx[k];
                    int y = j + dy[k];
                    if (x < 1 || x > n || y < 1 || y > m)
                        continue;
                    a[x][y] = max(a[x][y], 1ll);
                }
            }
        }
    }
    int cnt = 1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (a[i][j] <= 1)
                ans = max(ans, 1ll);
            if (a[i][j] == 0 && vis[i][j] == 0)
            {
                sum = 0;
                dfs(i, j, cnt);
                ans = max(ans, sum);
                cnt++;
            }
        }
    }
    cout << ans << endl;
    return 0;
}

T4

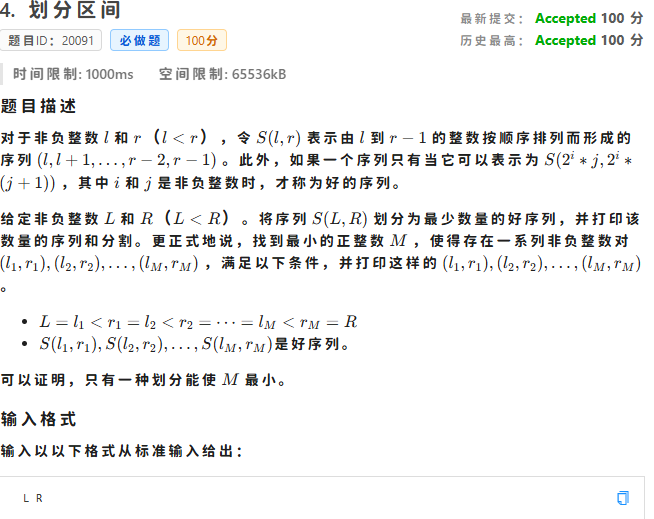
一个关于二进制的找规律数学（描述的有点抽象）

我们看题目给出的公式

\[S(2 ^ {i} × j, 2 ^ {i} × (j + 1)) \]

我们简单计算发现，这样子一个好区间的长度必然是 \(2 ^ {x}\)，而且，这个数还得是 \(l_i\) 的因数，我们需要让区间个数尽可能的少，即区间尽可能长，所以我们就可以把长度改为 \(2 ^ {x}\)， \(x\) 为 \(l_i\) 分解质因数后2的指数
code

#include <bits/stdc++.h>
#define int long long
using namespace std;
int l, r;
signed main()
{
    cin >> l >> r;
    vector <pair <int, int>> v;
    while (l < r)
    {
        int x = (1ll << 60);
        while (l % x != 0 || l + x > r)
        {
            x /= 2;
        }
        v.push_back({l, l + x});
        l += x;
    }
    cout << v.size() << endl;
    for (auto x : v)
    {
        cout << x.first << " " << x.second << endl;
    }
    return 0;
}

总结

这次模考我觉得还不错，该拿到的分都拿到了，还把T4调A了。第三题我觉得还是有点可惜，居然没有想到连通块的做法
分数：330
排名：7
AC：3
强省弱省都是一等奖抄袭一下CCCsuper