PAT 甲级1005【1005 Spell It Right】
用JAVA可以用BigInteger解决。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.math.BigInteger;
import java.util.HashMap;
import java.util.Map;
public class Main {
@SuppressWarnings("unchecked")
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BigInteger big = new BigInteger(br.readLine());
int sum = 0;
BigInteger x = big.add(BigInteger.ZERO);
while (x.compareTo(BigInteger.ZERO) > 0) {
int digit = x.mod(BigInteger.valueOf(10l)).intValue();
sum += digit;
x = x.divide(BigInteger.valueOf(10l));
}
Map<Integer, String> map = new HashMap<>();
map.put(0, "zero");
map.put(1, "one");
map.put(2, "two");
map.put(3, "three");
map.put(4, "four");
map.put(5, "five");
map.put(6, "six");
map.put(7, "seven");
map.put(8, "eight");
map.put(9, "nine");
String str = String.valueOf(sum);
for (int j = 0; j < str.length(); j++) {
int digit = str.charAt(j) - '0';
if( j != 0){
System.out.print(" ");
}
System.out.print(map.get(digit));
}
System.out.println();
br.close();
}
}
高精度计算
太长不看版：结尾自取模板……
定义
高精度计算（Arbitrary-Precision Arithmetic），也被称作大整数（bignum）计算，运用了一些算法结构来支持更大整数间的运算（数字大小超过语言内建整型）。
引入
高精度问题包含很多小的细节，实现上也有很多讲究。
所以今天就来一起实现一个简单的计算器吧。
任务
输入：一个形如 a <op> b 的表达式。
a、b分别是长度不超过
的十进制非负整数；<op>是一个字符（+、-、*或/），表示运算。- 整数与运算符之间由一个空格分隔。
输出：运算结果。
- 对于
+、-、*运算，输出一行表示结果； - 对于
/运算，输出两行分别表示商和余数。 - 保证结果均为非负整数。
存储
在平常的实现中，高精度数字利用字符串表示，每一个字符表示数字的一个十进制位。因此可以说，高精度数值计算实际上是一种特别的字符串处理。
读入字符串时，数字最高位在字符串首（下标小的位置）。但是习惯上，下标最小的位置存放的是数字的 最低位，即存储反转的字符串。这么做的原因在于，数字的长度可能发生变化，但我们希望同样权值位始终保持对齐（例如，希望所有的个位都在下标 [0]，所有的十位都在下标 [1]……）；同时，加、减、乘的运算一般都从个位开始进行（回想小学的竖式运算），这都给了「反转存储」以充分的理由。
此后我们将一直沿用这一约定。定义一个常数 LEN = 1004 表示程序所容纳的最大长度。
由此不难写出读入高精度数字的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
|
输出也按照存储的逆序输出。由于不希望输出前导零，故这里从最高位开始向下寻找第一个非零位，从此处开始输出；终止条件 i >= 1 而不是 i >= 0 是因为当整个数字等于 时仍希望输出一个字符 0。
1
2
3
4
5
6
7
|
|
拼起来就是一个完整的复读机程序咯。
copycat.cpp
四则运算
四则运算中难度也各不相同。最简单的是高精度加减法，其次是高精度—单精度（普通的 int）乘法和高精度—高精度乘法，最后是高精度—高精度除法。
我们将按这个顺序分别实现所有要求的功能。
加法
高精度加法，其实就是竖式加法啦。
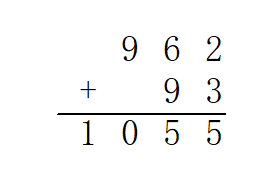
也就是从最低位开始，将两个加数对应位置上的数码相加，并判断是否达到或超过 。如果达到，那么处理进位：将更高一位的结果上增加 ，当前位的结果减少 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
|
试着和上一部分结合，可以得到一个加法计算器。
adder.cpp
减法
高精度减法，也就是竖式减法啦。
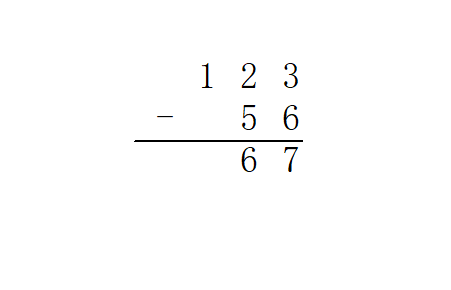
从个位起逐位相减，遇到负的情况则向上一位借 。整体思路与加法完全一致。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
|
将上一个程序中的 add() 替换成 sub()，就有了一个减法计算器。
subtractor.cpp
试一试，输入 1 2——输出 /9999999，诶这个 OI Wiki 怎么给了我一份假的代码啊……
事实上，上面的代码只能处理减数 大于等于被减数 的情况。处理被减数比减数小，即 时的情况很简单。
要计算 的值，因为有 ，可以调用以上代码中的 sub 函数，写法为 sub(b,a,c)。要得到 的值，在得数前加上负号即可。
乘法
高精度—单精度
高精度乘法，也就是竖……等会儿等会儿！
先考虑一个简单的情况：乘数中的一个是普通的 int 类型。有没有简单的处理方法呢？
一个直观的思路是直接将 每一位上的数字乘以 。从数值上来说，这个方法是正确的，但它并不符合十进制表示法，因此需要将它重新整理成正常的样子。
重整的方式，也是从个位开始逐位向上处理进位。但是这里的进位可能非常大，甚至远大于 ，因为每一位被乘上之后都可能达到 的数量级。所以这里的进位不能再简单地进行 运算，而是要通过除以 的商以及余数计算。详见代码注释，也可以参考下图展示的一个计算高精度数 乘以单精度数 的过程。
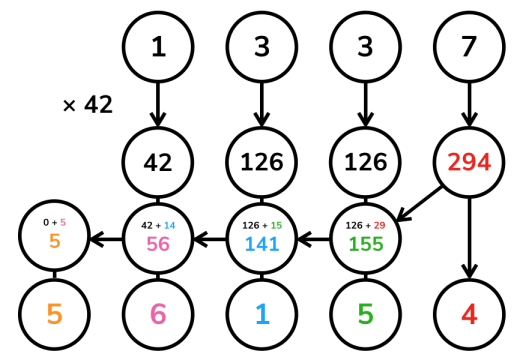
当然，也是出于这个原因，这个方法需要特别关注乘数 的范围。若它和 （或相应整型的取值上界）属于同一数量级，那么需要慎用高精度—单精度乘法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
|
高精度—高精度
如果两个乘数都是高精度，那么竖式乘法又可以大显身手了。
回想竖式乘法的每一步，实际上是计算了若干 的和。例如计算 ，计算的就是 。
于是可以将 分解为它的所有数码，其中每个数码都是单精度数，将它们分别与 相乘，再向左移动到各自的位置上相加即得答案。当然，最后也需要用与上例相同的方式处理进位。
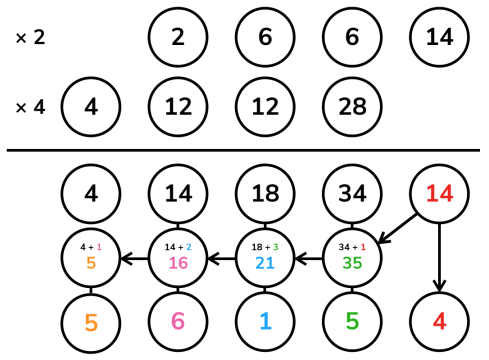
注意这个过程与竖式乘法不尽相同，我们的算法在每一步乘的过程中并不进位，而是将所有的结果保留在对应的位置上，到最后再统一处理进位，但这不会影响结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
|
除法
高精度除法的一种实现方式就是竖式长除法。
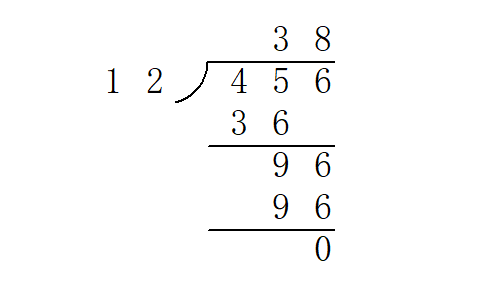
竖式长除法实际上可以看作一个逐次减法的过程。例如上图中商数十位的计算可以这样理解：将 减去三次 后变得小于 ，不能再减，故此位为 。
为了减少冗余运算，我们提前得到被除数的长度 与除数的长度 ，从下标 开始，从高位到低位来计算商。这和手工计算时将第一次乘法的最高位与被除数最高位对齐的做法是一样的。
参考程序实现了一个函数 greater_eq() 用于判断被除数以下标 last_dg 为最低位，是否可以再减去除数而保持非负。此后对于商的每一位，不断调用 greater_eq()，并在成立的时候用高精度减法从余数中减去除数，也即模拟了竖式除法的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
|