最大流学习笔记
定义
一张有向带权图\(G=(V,E)\),一个源点\(S\),一个汇点\(T\),构成一个网络。边的权值\(c(x,y)\)称为边的容量。另外,定义\(f\)为\(G\)的可行流,当且仅当对于原图的任意一条边\((x,y)\),其流量\(f(x,y)\)满足以下条件:
1.\(f(x,y)≤c(x,y)\) (容量限制)
2.\(∀x≠S,x≠T\),有\(\sum_{(u,x)∈E}f(u,x)=\sum_{(x,v)∈E}f(x,v)\) (流量守恒)
可行流可以形象地理解为水流,容量限制为水管的粗细,流入一个节点的水流总和必然等于流出的总和。
所谓最大流,指的是使得\(\sum_{(S,v)∈E}f(S,v)\)最大的可行流。即使得源点流出的流量最大。同样根据流量守恒定律,此时流入汇点的流量也是最大的。
求解
EK算法
定义边的剩余容量为\(c(x,y)-f(x,y)\)。那么对于任意的可行流,若能找到一条从源点到汇点的路径,使得经过的所有边上的剩余容量都大于0,那么显然可以让一股流加入到可行流中,使流量增大。我们称这样的路径为增广路。显然,若一个可行流没有增广路,那么它就是最大流。EK算法通过不断寻找一个可行流的增广路并更新当前可行流,实现答案的求解。
残留网络(残量网络)
定义残留网络\(G'\)为原图\(G\)关于一个可行流\(f\)的单射。对于\(G\)中的一条边\((x,y)\),\(G'\)中对应的边权\(f'(x,y)=c(x,y)-f(x,y)\),同时建立反向边,\(f'(y,x)=f(x,y)\)。显然有\(f'(x,y)+f'(y,x)=c(x,y)\)。
至此,你可能并不理解为什么要引入这么多的概念,甚至容易产生混淆。但实际上,残留网络的引入是为了更加简便地修改可行流,EK算法在寻找增广路并更新答案的过程中,不断维护新的残留网络。残留网络上的增广路,在原图中的含义十分巧妙,实现了增加流量与减少流量(注意,指的是一条边的流量,而非总流量)的完美契合,大大降低了算法的复杂程度。至于在残留网络上建立反向边,实际上是为了“反悔”。因为在找到了一条增广路后,将其全部“填满”并不一定是全局最优解,容易举出反例。
来看EK算法的实现过程:
1.残留网络最开始为:对于正向边,权值等于原图中的容量;对于反向边,权值为0。
2.在残留网络上找到一条增广路,计算出路径上各边边权的最小值\(minf\),将路径上各边边权-\(minf\),将这些边的反向边边权+\(minf\)。
3.重复以上操作,直到不存在增广路为止。此时原图中各边的流量等于残留网络中其反向边的权值。
图解:(图中省略边权为0的边)
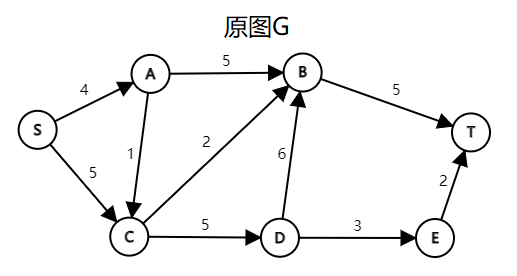
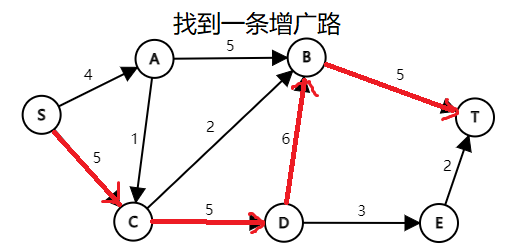
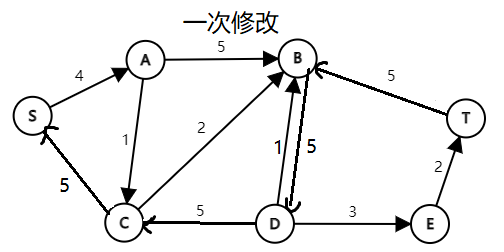
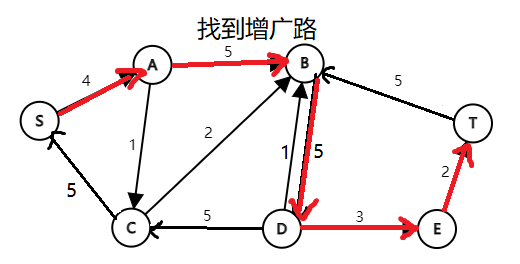
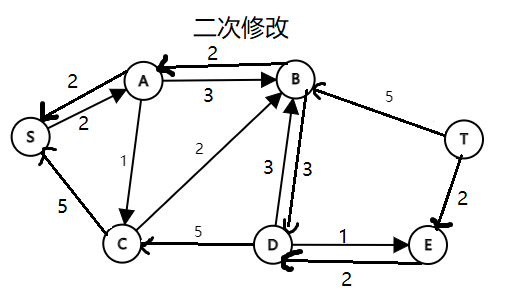
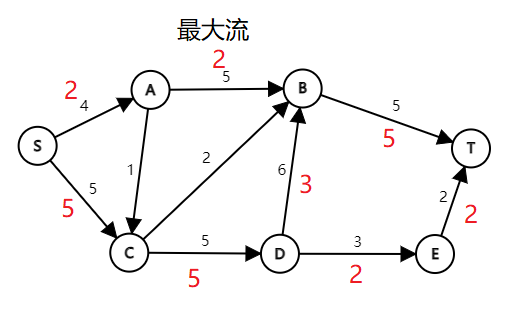
(PS:第一次发这么多图,没有经验,应该合在一张图里发的……观看体验可能极差,请多包含[抱拳])
可以发现,在第一次修改后,\((D,B)\)的流量为5。但是这却浪费了下方的容量空间,不是最优解。此时反向边\((B,D)\)就大有用处了,它与\((D,E)、(E,T)\)一起构成了新的增广路。二次修改后,相等于在之前可行流的基础上,将(D,B)的流量减少2,(D,E)(E,T)的流量增加2。而由D点流入B点减少的2,则由A点补充。仔细体会残留网络中修改边权的操作,我们可以形象地理解为:正向边代表剩余容量,反向边代表可以反悔的最大容量。
EK算法时间复杂度为\(O(nm^2)\)。但实际上远达不到这个上界,一般能够处理\(10^3\)~\(10^4\)规模(边数+点数)的网络。
Code
值得一提的是,在处理反向边时,我们采用“成对存储”的技巧。2和3,4和5,6和7……之间可以通过xor 1的运算相互得到。于是可以快速找到反向边。
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1e3 + 5;
const int M = 2e4 + 5;
const int INF = 0x7fffffff;
int n, m, s, t, maxflow;
int head[N], nxt[M], ver[M], edge[M], tot = 1;
int incf[N], pre[N], v[N];
void Add(int x, int y, int z) {
nxt[++tot] = head[x]; head[x] = tot; ver[tot] = y; edge[tot] = z;
}
bool bfs() {
memset(v, 0, sizeof (v));
queue<int> q;
q.push(s); v[s] = 1; incf[s] = INF;
while (!q.empty()) {
int x = q.front(); q.pop();
for (int i = head[x]; i; i = nxt[i])
if (edge[i]) {
int y = ver[i];
if (v[y]) continue;
incf[y] = min(incf[x], edge[i]);
pre[y] = i;
if (y == t) return 1;
v[y] = 1; q.push(y);
}
}
return 0;
}
void Update() {
int x = t;
while (x != s) {
int i = pre[x];
edge[i] -= incf[t];
edge[i ^ 1] += incf[t];
x = ver[i ^ 1];
}
maxflow += incf[t];
}
int main() {
scanf("%d%d%d%d", &n, &m, &s, &t);
while (m--) {
int u, v, c;
scanf("%d%d%d", &u, &v, &c);
Add(u, v, c); Add(v, u, 0);
}
while (bfs()) Update();
printf("%d\n", maxflow);
return 0;
}
最大流问题一般注重建模,建立网络之后,剩下套模板。由于EK算法不如Dinic高效,一般除了费用流用EK算法,不会使用EK的模板。
Dinic算法
Dinic是对EK的优化。注意到EK每次只寻找一条增广路,更新完后再重头寻找,效率较低。于是Dinic建立了一张分层图。用\(d[x]\)表示\(S\)到点\(x\)最少经过的步数,显然可以用bfs求出。Dinic再在分层图上用dfs寻找增广路,回溯时更新残留网络的边权。
Dinic时间复杂度为\(O(n^2m)\),实际效率也要高于EK,能处理\(10^4\)~\(10^5\)规模的网络。一般采用Dinic作为最大流的模板。
在上述基础上,Dinic还加入了一些剪枝,如“当前弧优化”。它们的作用都是为了防止重复遍历无法达到\(T\)的路径。详见代码。
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1e4 + 5;
const int M = 2e5 + 5;
const int INF = 0x3f3f3f3f;
int n, m, s, t, d[N], cur[N];
int head[N], nxt[M], ver[M], edge[M], tot = 1;
void Add(int x, int y, int z) {
nxt[++tot] = head[x]; head[x] = tot; ver[tot] = y; edge[tot] = z;
}
bool bfs() {
memset(d, 0, sizeof (d));
queue<int> q;
q.push(s); d[s] = 1; cur[s] = head[s];
while (!q.empty()) {
int x = q.front(); q.pop();
for (int i = head[x]; i; i = nxt[i]) {
int y = ver[i];
if (edge[i] && !d[y]) {
d[y] = d[x] + 1;
cur[y] = head[y];
if (y == t) return 1;
q.push(y);
}
}
}
return 0;
}
int dinic(int x, int limit) {
if (x == t) return limit;
int flow = 0;
for (int i = cur[x]; i && flow < limit; i = nxt[i]) {
cur[x] = i;
int y = ver[i];
if (edge[i] && d[y] == d[x] + 1) {
int v = dinic(y, min(limit - flow, edge[i]));
if (!v) d[y] = 0;
edge[i] -= v;
edge[i ^ 1] += v;
flow += v;
}
}
return flow;
}
int main() {
scanf("%d%d%d%d", &n, &m, &s, &t);
while (m--) {
int u, v, c;
scanf("%d%d%d", &u, &v, &c);
Add(u, v, c); Add(v, u, 0);
}
int maxflow = 0, flow;
while (bfs()) while (flow = dinic(s, INF)) maxflow += flow;
printf("%d\n", maxflow);
return 0;
}
应用
最大流&二分图
此前我们求解二分图使用匈牙利算法,现在不妨使用最大流分析。我们建立一个虚拟的源点\(S\)和汇点\(T\),将\(S\)向左部所有点连一条容量为1的边,右部所有点向\(T\)连一条容量为1的边,左右部之间不连无向边,而是左部向右部连容量为1的边。容易证明,最大匹配数=最大流量。
同时,最大流可以轻松解决匈牙利算法不能解决的二分图多重匹配问题。只需改变\(S\)向左部的边的容量为\(k_{l_i}\),右部向\(T\)的容量为\(k_{r_j}\),问题即刻解决。
另外,我们可以使用最大流求出二分图最大匹配的必须边与可行边。
在一张二分图中,最大匹配的方案不是唯一的。若所有最大匹配都包含\((x,y)\),那么称\((x,y)\)为必须边;若\((x,y)\)至少被一种方案包含,那么称其为可行边。
我们先来看最大匹配=完备匹配的情况。可以参考这篇题解国王的任务。这题要求求出所有可行边。类似地,我们也可以得到必须边的判定条件。
1.\((x,y)\)是必须边⇔\((x,y)\)是当前二分图的匹配边,且\(x\),\(y\)属于不同强联通分量。
2.\((x,y)\)是可行边⇔\((x,y)\)是当前二分图的匹配边,或\(x\),\(y\)属于同一强连通分量。
那么在更加普遍的情况,即最大匹配不一定等于完备匹配的情况下,上述结论不成立。因为在\((x,y)\)断开连接后,\(y\)的匹配点不再必要和\(x\)构成增广路。这种情况下,就需要用到最大流。
设\((u,v)\)是一匹配边,\(z\)是右部一非匹配点,那么在残留网络中,\((v,u)\)权值为1,\((z,T)\)的权值为1。设\(v\)当前是匹配点,那么\((T,v)\)的权值为1。那么存在路径\(z→T→v\)。此时若二分图中\(u\)到\(z\)有增广路,则残留网络上\(u\)能到达\(z\),进而到达\(v\)。那么在残留网络中,\(u\)和\(v\)仍在同一强联通分量中。左部点通过\(S\)连接同理。
综上,在一般的二分图中:
1.\((x,y)\)是必须边⇔\((x,y)\)在残留网络中权值为1,且在残留网络上属于不同强联通分量。
2.\((x,y)\)是可行边⇔\((x,y)\)在残留网络中权值为1,或在残留网络上属于同一强联通分量。
例:舞动的夜晚
最小割
在一个网络中,删去一些边使得\(S\)与\(T\)不连通。删去的最小边权总和为最小割。
定理:最小割=最大流。
证明:易证。
例:Cable TV Network
给定一张无向图,问最少删去几个点,使图不连通。一张图不连通,至少有两点不连通,我们可以枚举这两点,设为\(S\)和\(T\)。答案为所有结果中的最小值。
此题要求删点,而最小割要求删边。这里用到了网络流建模的常用技巧之一:点边转化。我们将每个点拆成“入点”和“出点”,将点的属性体现在入点与出点之间的边上。
在这题中,我们可以在入点和出点之间连容量为1的边,剩下所有不同点之间的无向边,转化为入点与出点之间两条有向边,权值为+∞。于是“删点”就转化为“删边”了。因为我们要保证删去的边一定是同一点的入点和拆点之间的边,那么将其他边设为+∞,可以防止删去其他边。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号