Java数据结构与算法 - 外部存储
Q: 什么是外部存储?
A: 外部存储特指某类磁盘系统,例如在大多数台式电脑或服务器中的硬盘。
Q: 如何访问外部存储?
A: 我们所学的数据结构都是假设数据存储在内存中,但是,在很多情况下要处理的数据量太大,不能都存储在内存中。这种情况下需要另一种存储方式,访问外部磁盘文件上的数据。外部磁盘存储的缺点就是读写比内存要慢得多,因此需要用一个合理的数据结构技术来管理它们。
A: 作为外部存储的一个例子,假设编写一个数据库程序来管理一个电话簿,可能有500000条记录。每条记录包括姓名、地址、电话号码以及公司内部使用的各种其他数据。每条内容存储一条记录,长度为512字节,则文件大小是500000 * 512, 256000000字节,即256M。假设对计算机内存来说这个数据太大以至于存储不下,不过磁盘驱动器足够大可以存储它。
A: 因此,在磁盘驱动器中保存了大量的数据,怎么组织它们来实现以下的特点:快速查找、插入和删除?为了找到答案,需要牢记两条,第一,在磁盘驱动器中访问数据比在内存中要慢得多;第二,一次访问很多数据。
非常慢得访问。计算机的内存按电子的方式工作,几微妙就可以访问一个字节,而磁盘驱动器存取就要复杂得多,需要在旋转的磁盘上,读写头先要移动到正确的磁道,通过先进的电动机或类似的设备完成访问磁盘驱动器上的某个数据。
一旦找到正确的磁道,读写头必须要等待数据旋转到正确的位置,平均来说,这一步要旋转半圈,即使磁盘每分钟转10000圈,那么在读到数据前还需要3毫秒。读写头就位后,就可以进行实际的读/写操作了,因此通常磁盘存取的时间大约是10毫秒,大约比访问内存慢了10000倍。
一次访问很多数据。当读写头到达正确的位置后开始读(或写)过程,驱动器很快就把大量数据转移到内存中,为了简化驱动器的控制装置,在磁盘上的数据按块存储。
磁盘驱动器每次最少读或写一个数据块的数据。块的大小根据操作系统,磁盘驱动器的容量,以及其他因素而不同,但它总是2的倍数。在电话本的例子里,假设一个数据块的容量是8192字节(2^13)。因此电话本数据库中需要256000000字节分为8192字节每块,一共是31250块。
在读/写操作时如果按块容量的倍数来操作是效率最高的。如果要读100个字节,系统读取一块8192字节,只留100字节,把其他的都扔掉。或者如果要读取8200字节,它会读两块,第二块只留8字节,剩余的全部扔掉。通过组织软件使它每次操作一块数据,可以优化性能。
A: 假设电话本记录的大小是512字节,在一块中存储可以16条记录(8192除以512),如下图所示,因此效率最高的情况是一次读取16条记录(或这个数字的倍数)。 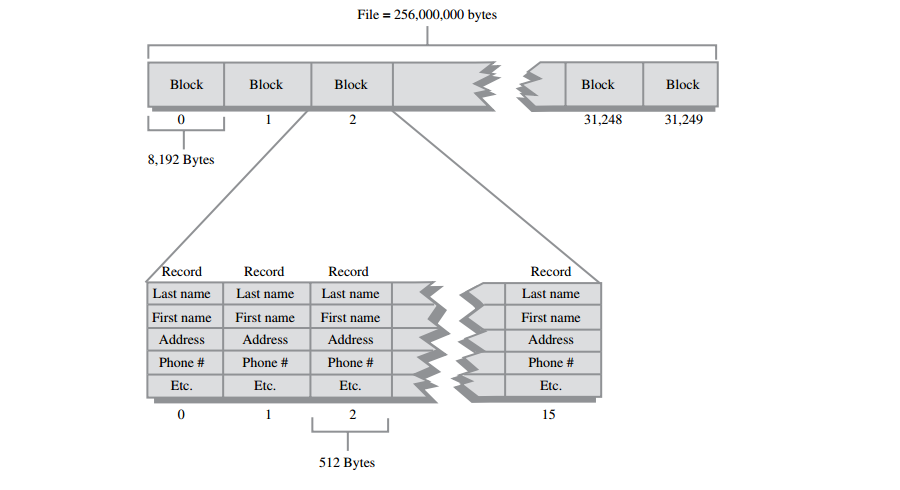
注意让记录的大小是2的倍数也是很有用的,这样做,每块可以正好装下整数个记录。
Q: 使用顺序有序排列进行访问?
A: 排列电话本数据的一种方法是在磁盘文件中按照某个关键字为所有的记录排序,如按照姓的字典序。 
A: 查找。在顺序有序排列的文件中查找某个姓的记录,如Smith,可以用二分查找方法。在内存中有8192字节的缓冲区,一次把一块中的16个记录都读到缓冲区里。如果这些记录的关键字在字典序中位置靠后(例如,Keller),就到文件的3/4处来读取那里的一块;如果关键字靠前,就到文件的1/4处(例如,Deleon)读取。不断把范围缩小一半,最后会找到要找的记录。
对于500000个数据项,在内存中使用二分查找要执行log2N次比较,即19次比较。如果每次比较要10微妙,总共就是190微妙,比眨一下眼睛还要快。
磁盘存取比内存存取慢得多,但另一方面一次访问一块,块数比记录要少得多,在电话本的例子里,有31250块,它取2的对数大约是15,所以理论上大约需要存取15次磁盘来找到想要的记录。实际上这个数字还要小一点,因为要找下一个记录时,有可能还在缓冲区的块上,这就减少了大约两次的磁盘次数。因此需要大约13次磁盘存取(15-2),每次访问需要10毫秒,总共需要130毫秒。这比内存访问要慢得多,但还不算太差。
A: 插入。在顺序有序排列的文件插入(或删除)一个数据项时情况要糟糕很多。因为数据是有序的,插入(或删除)操作平均需要移动一半的记录,因此要移动大概一半的块。移动每块都需要存取两次磁盘:一次读和一次写。假设有31250块,需要读和写(平均)15625块,每次读和写需要10毫秒的话总共用5分钟来插入一条记录。如果要在电话本中插入上千条新名字,这显然太不理想了。
A: 顺序有序排列的另一个问题是,如果它只有一个关键字,速度还比较快:比如这里的文件是按照姓排序的,但是假设需要查找某个电话号码,就不能用二分查找,因为数据是按姓排序的,这就得整个文件查找,用顺序访问的方法一块一块地找。这样查找需要读取平均一半的块,大约会需要2.5分钟,对于一个简单的查找来说也是非常糟糕的。所以要寻找一种更有效的方法来保存磁盘中的数据。
Q: 什么是B-树?
A: 1972年R.Bayer和E.M.McCreight首先提出了B-树作为外部存储的数据结构。B-树是一棵多叉树,有点像2-3-4树,只不过它的每个节点有更多的数据项和更多的子节点。
A: 前面已经讲过一次读或写一个数据块效率是最高,在B-树中,一个数据块就是一个节点,这样做的意义是读取一个节点可以在最短时间里访问到最大数据量的数据。在磁盘文件中存储的B-树,节点间的链接是用文件中的块的编号表示,在电话本的例子中,每条数据记录512字节,可以把16条记录放在一个8192字节的块中。因此块编号从0~31249。可以用一个int型的字段保存块号码,int是4个字节,可以保存20亿以上的块号码,基本上对大多数的文件都够用了。
A: 不过考虑到保存指向子节点的引用也需要存储空间,因此把块中记录的数量减少到15,这样就有地方保存链接,不过更高效的方法是每个节点保存偶数个记录,这样把记录大小减少为507字节,一个块16个记录,507*16,8112字节,省出80个字节作为保存引用。而一个块对应一个节点,每个节点将有17个子节点数链接,这些链接则需要17*4, 68字节,刚好是我们省出80个字节能保存起来。那么一个节点总共就需要507*16+68, 8180个字节,还剩余12个字节的空间。
A: 在每个节点中数据是按关键字顺序有序排列,像2-3-4树一样,B-树的阶数由节点拥有最多的子节点数决定。在电话本的例子里是17,所以这个树是17阶B-树。如下图, 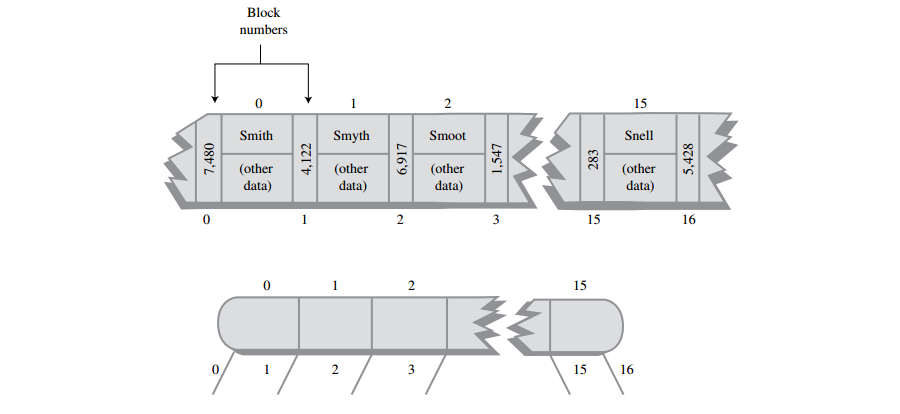
Q: B-树的查找(Searching)?
A: A search for a record with a specified key is carried out in much the same way it is in an in-memory 2-3-4 tree.
First, the block containing the root is read into memory. The search algorithm then starts examining each of the 15 records (or, if it’s not full, as many as the node actually holds), starting at 0. When it finds a record with a greater key, it knows to go to the child whose link lies between this record and the preceding one.
Q: B-树的插入?
A: In a B-tree it’s important to keep the nodes as full as possible so that each disk access, which reads an entire node, can acquire the maximum amount of data. To help achieve this end, the insertion process differs from that of 2-3-4 trees in three ways:
- A node split divides the data items equally: Half go to the newly created node, and half remain in the old one.
- Node splits are performed from the bottom up, as in a 2-3 tree, rather than from the top down.
- Again, as in a 2-3 tree, it’s not the middle item in a node that’s promoted upward, but the middle item in the sequence formed from the items in the node plus the new item
A: 通过建立一棵小的B-树来示范插入过程,如下图,因为没有那么大的空间来显示每个节点中的记录的实际数量,所以节点中只有4个记录,因此这是一颗5阶B-树。
为了决定新数据项要插在哪里,插入算法在内部缓冲区会把这5个关键字进行排序,如下图,一个箭头表示的中间数据项要上移,中间数据项的左边留在原分裂的节点,中间数据项的右边要移到右边的新节点(在电话本例子中,8个数据项会移动每个子节点) 
注意在整个这次插入过程中,没有任何一个节点(除了根)的数据项少于一半,并且很多都比一半要满。
Q: B-树的效率?
A: 在电话本的例子里有500000条记录,B-树中所有的节点至少是半满的,所以每个节点至少有8条记录和9个子节点的链接。树的高度因此比log9N小一点,结果为5.972,这样树的高度大概是6层。因此,使用B-树中需要6次访问磁盘就可以在有500000条记录的文件中找到任何记录,每次访问10毫秒,这就需要花费60毫秒的时间,这比在顺序有序排列的文件中二分查找要快得多。
A: 再来说插入的情况。
先假设B-树不需要节点分裂的情况,在电话本示例中,已经看到只需要6次访问就可以找到插入点,之后还需要1次访问把保存了新插入记录的块写回磁盘,一共是7次访问。
接下来看看节点需要分裂的情况,要读入分裂的节点,它的一半记录(8个)都要移动,并且要写回磁盘。新创建的节点要写入磁盘,必须要读取父节点,然后插入上移的记录,写回磁盘,这里就有5次访问,加上找到插入点需要6次访问,一共是12次。相比在访问顺序文件中插入数据项所需要的500000次访问这是大大地改进了。
Q: 索引?
A: 另一种加快文件访问速度的方法是使用索引。文件索引是由关键字-块号码组成的列表,它按关键字排序。关键字用28个字符长度的字符串来保存,块号码还是int整型,因此,索引中的每一个元素需要32个字节。 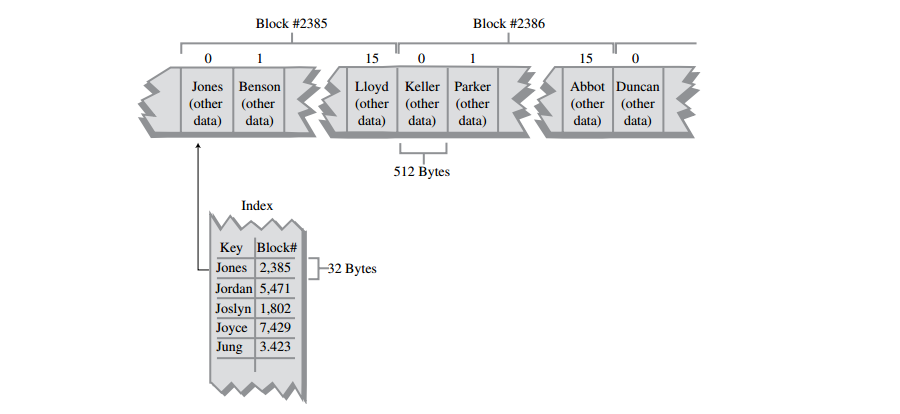
索引比文件中实际记录小得多,它甚至可以完全放在内存中,在电话本示例中,索引的大小是32 * 31250,1000000字节,即0.95M,把它放到现在的计算机的内存中不会有任何问题。
Q: 索引保存在磁盘上?
A: 索引可以保存在磁盘上,数据库程序启动后就读取到内存中来,这样,对索引的操作就可以在内存中完成了。每天结束时(或更频繁,如每小时)将索引写回磁盘中永久保存。
Q: 索引的查找?
A: 在电话本示例中,二分查找需要19次索引访问,每次访问20微妙,这样只需要大约4/10000秒,然后在索引中找到实际的记录块的号码后,不可避免要花时间从文件访问它,不过,这一次访问磁盘的时间只需要10毫秒。
Q: 索引的插入?
A: 需要做两步:
1) 把这个数据项的整个记录插入到主文件中;
2) 把关键字和包括新数据项存储的块号码插入到索引中;
因为索引是顺序有序排列,要插入新数据项,平均需要移动一半的索引记录,设内存中2微妙移动一个字节,则需要250000 * 32 * 2,大约16秒来插入一个新记录。这比没有索引,在顺序有序排列的文件插入一个新记录要5分钟明显好多了。另外注意不需要移动主文件中的记录,只要在文件末尾处添加一条新纪录即可。
Q: 什么是多级索引?
A: 索引的有一个优点,就是可以创建多级索引。同一个文件可以创建不同关键字的索引,可以创建按姓进行排序的索引,也可以创建按地址进行排序的索引等等。索引和文件比起来很小,所以它并不会大量地增加数据存储量。
Q: 对内存来说索引太大怎么办?
A: 如果索引太大,不能放在内存中,它就需要按块分开存储在磁盘上。对大文件来说把索引保存成B-树是很合适的,主文件中的记录可以存成任何合适的顺序。 注意索引按B-树存储时,每个节点保存了n个子节点指针和n - 1个数据项,每个数据项保存关键字和指向主文件中的一个块的指针,不要把这两种类型的块指针搞混淆。
Q: 组合搜索条件的可行方法?
A: Suppose in our phone book example we wanted a list of all entries in the phone book with first name Frank, who lived in Springfield, and who had a phone number with three 7 digits in it. (These were perhaps clues found scrawled on a scrap of paper clutched in the hand of a victim of foul play.)
组合搜索唯一可行的方法就是顺序地读取文件中的每一个块,检查每个记录看看它是否符合查找的条件。如果仅根据姓排列文件一点用都没有,甚至如果有索引文件,按名字和程序排序,也不能很方便地找到含有Frank和SpringField的记录。
Q: 外部文件的排序?
A: 归并排序是外部数据排序的首选。因为这种方法比其他大部分的排序方法来说,磁盘访问更多的涉及临近的记录而不是文件中随机的部分。要做到这一点需要做到两步:
1) 读取一块,它的记录在内部排序,然后把排完序的块写回到磁盘中,下一块也同样排序并写回到磁盘中。直到所有的块内部都有序为止。
2) 读取两个有序的块,合并成一个两块的有序的序列,再把它们写回磁盘。下次把每两块序列合并成四块一起的序列,将这个过程继续下去,直到所有成对的块合并过为止。每次有序序列的长度增长一倍,直到整个文件有序。
A: 如下图是对一个外部文件使用归并排序的过程。文件含有4块,每块有4个记录,一共有16条记录。 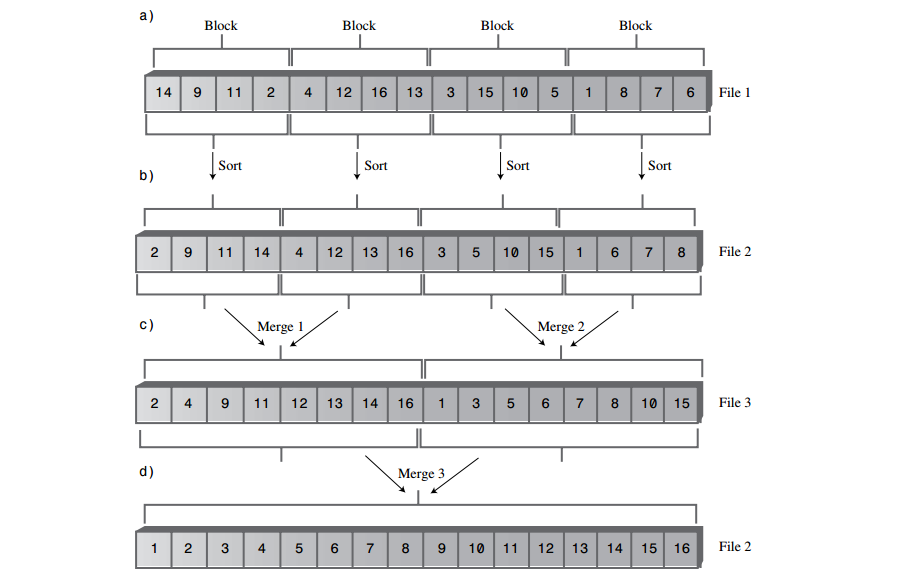
A: 块的内部排序可以用任何排序方法,如快速排序、插入排序。一般考虑使用第二个文件File2来保存有序的块,通常希望避免改变初始文件的内容。
A: 注意上图只使用3个文件就能完成整个外部文件的排序。File2和File3都是交替进行文件内部、相邻块与块之间合并的排序处理。
Q: 本篇总结?
A:
- 外部存储的意思是在内存外面保存数据,通常是在磁盘上
- 外部存储器比内存大,便宜,但是慢
- 外部存储器中的数据通常需要在内存间来回传送,一次传送一块
- 在外部存储器里的数据可以按关键字顺序有序排列,这样查找很快,但插入(或删除)很慢
- B-树是多叉树,每个节点可以有几十或上百个关键字和子节点
- B-树中的子节点的个数总是比关键字数据项的个数多1
- 为达到最好的性能,B-树通常在一个节点中保存一块的数据
参考
- 《Java数据结构和算法》第10章 - 外部存储



 浙公网安备 33010602011771号
浙公网安备 33010602011771号