算法导论：动态规划

多阶段决策问题

求解的问题可以划分为一系列相互联系的阶段，在每个阶段都需要作出决策，且一个阶段决策的选择会影响下一个阶段的决策，从而影响整个过程的活动路线，求解的目标是选择各个阶段的决策使整个过程达到最优。

基本概念

• 阶段：把所给的问题的求解过程恰当地划分为若干个相互联系的阶段
• 状态：表示每个阶段开始时，问题或系统所处的客观状况。状态既是该阶段的某个起点，又是前一个阶段的某个终点。通常一个阶段有若干个状态。
• 状态的无后效性：如果某阶段状态给定后，则该阶段以后过程的发展不受该阶段以前各阶段状态的影响，也就是说状态具有马尔科夫性
• 策略：各个阶段决策的确定后，就组成了一个决策序列，该序列称之为一个策略。由某个阶段开始到终止阶段的过程称为子过程，其对应的某个策略称为子策略。

最优化原理

求解问题的一个最优策略序列的子策略序列总是最优的，则称该问题满足最优性原理。

对具有最优性原理性质的问题而言，如果有一决策序列包含有非最优的决策子序列，则该决策序列一定不是最优的。

最优性原理判别

设 \(G\) 是一个有向加权图，则 \(G\) 从顶点 \(i\) 到顶点 \(j\) 之间的最短路径问题满足最优性原理

反证法：

设 \(i-i_p-i_q-j\) 是一条最短路径，但其中子路径 \(i_p-i_q-j\) 不是最优的

假设最优路径是 \(i_p-i_q'-j\)，则重新构造一条路径 \(i-i_p-i_q'-j\)

显然路径 \(i-i_p-i_q'-j\) 长度小于路径 \(i-i_p-i_q-j\)，但这与路径 \(i-i_p-i_q-j\) 是最短路径矛盾

所以该问题满足最优性原理

最长路径问题不满足最优性原理

反例：

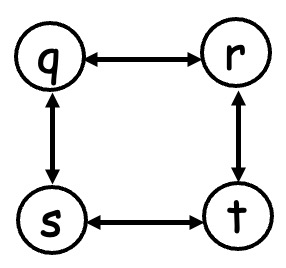
\(q-r-t\) 是 \(q\) 到 \(t\) 的最长路径

\(q-s-t-r\) 是 \(q\) 到 \(r\) 的最长路径

\(r-q-s-t\) 是 \(r\) 到 \(t\) 的最长路径

但是 \(q\) 到 \(r\) 的最长路径和 \(r\) 到 \(t\) 的最长路径合并起来并不是 \(q\) 到 \(t\) 的最长路径

所以，该问题不满足最优性原理。

基本思想

动态规划的思想实质是分治思想和解决冗余。

• 与分治法类似的是：将原问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
• 与分治法不同的是：经分解的子问题往往不是互相独立的。若用分治法来解，有些共同部分（子问题或子子问题）会被重复计算了很多次。

动态规划用一个表来记录所有已解的子问题的答案。

求解步骤

1. 找出最优解的性质，并刻画其结构特征
2. 递归地定义最优值（写出动态规划方程）
3. 以自底向上的方式计算出最优值
4. 根据计算最优值时记录的信息，构造最优解

适用条件

动态规划法的有效性依赖于问题本身所具有的两个重要的适用性质：

• 最优子结构：问题的最优解是由其子问题的最优解来构造
• 重叠子问题：在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次

背包问题

问题描述

• 给定 \(n\) 个物品：
  • 整数容量：\(w_1,w_2,...,w_n\)
  • 价值：\(v_1,v_2,...,v_n\)
• 具有整数 \(w\) 容量的背包

目标：寻找最优价值的子集可以放入背包中。

最优性原理判别

以 \(0-1\) 背包问题 \(Knap(1,n,c)\) 为例

\[\begin{cases} \sum_{i=l}^nw_ix_i\leq{c} \\ x_i\in{\left\{0,1\right\}},l\leq{i}\leq{n} \end{cases} \Longrightarrow{Knap(l,n,c)} \]

设 \((y_1,y_2,...,y_n)\) 是 \(Knap(1,n,c)\) 的一个最优解，\((y_2,...,y_n)\) 是 \(Knap(2,n,c-w_1y_1)\) 子问题的一个最优解。

如果不是子问题的最优解，则设 \((z_2,...,z_n)\) 是 \(Knap(2,n,c-w_1y_1)\) 子问题的一个最优解。则有：

\[\sum_{i=2}^nv_iz_i>\sum_{i=2}^nv_iy_i且\sum_{i=2}^nw_iz_i\leq{c-w_1y_1} \\ \Longrightarrow{v_1y_1+\sum_{i=2}^nv_iz_i>\sum_{i=1}^nv_iy_i}且w_1y_1+\sum_{i=2}^nw_iz_i\leq{c} \]

这说明 \((y_1,z_2,...,z_n)\) 是 \(Knap(1,n,c)\) 的一个最优解，与假设矛盾，故满足最优性原理。

解题思路

假设我们已经求解了在前 \(i-1\) 个物品中选择组合，放入容量为 \(j(j\leq{W})\) 的背包中的问题，这个问题的解是 \(V[i-1,j]\)。

则递推关系：

\[v[i,j]= \begin{cases} max\left\{V[i-1,j],v_i+V[i-1,j-w_i]\right\} & 0\leq{j-w_i} \\ V[i-1,j] & 0>j-w_i \end{cases} \]

初始条件：\(V[0,j]=0;V[i,0]=0\)

举例

背包容量 \(W=5\)

物品	体积	价值
1	2	12
2	1	10
3	3	20
4	2	15

解如下，横坐标表示容量 \(j\)，纵坐标表示前 \(i\) 个物品：

0	1	2	3	4	5
0	0	0	0	0	0
0	0	12	12	12	12
0	10	12	22	22	22
0	10	12	22	30	32
0	10	15	25	30	37

伪代码

int[][] DPKnapsack(int[] w, int[] v, int W, int n) {
	for(int j = 0; j <= W; j++) V[0][j] = 0;
	for(int i = 0; i <= n; i++) V[i][0] = 0;
  for(int i = 1; i <= n; i++) {
  	for(int j = 1; j <= W; j++) {
    	if(w[i] <= j && v[i] + V[i-1][j-w[i]] > V[i-1][j]) {
      	V[i][j] = v[i] + V[i-1][j-w[i]];
      }
      else V[i][j] = V[i-1][j];
    }
  }
  return V;
}

切杆问题

问题描述

给定一段长度为 \(n\) 英寸的钢条和一个价格表 \(p_i(i=1,2,…,n)\)，求切割钢条方案，使得销售收益 \(r_n\) 最大。

例如：

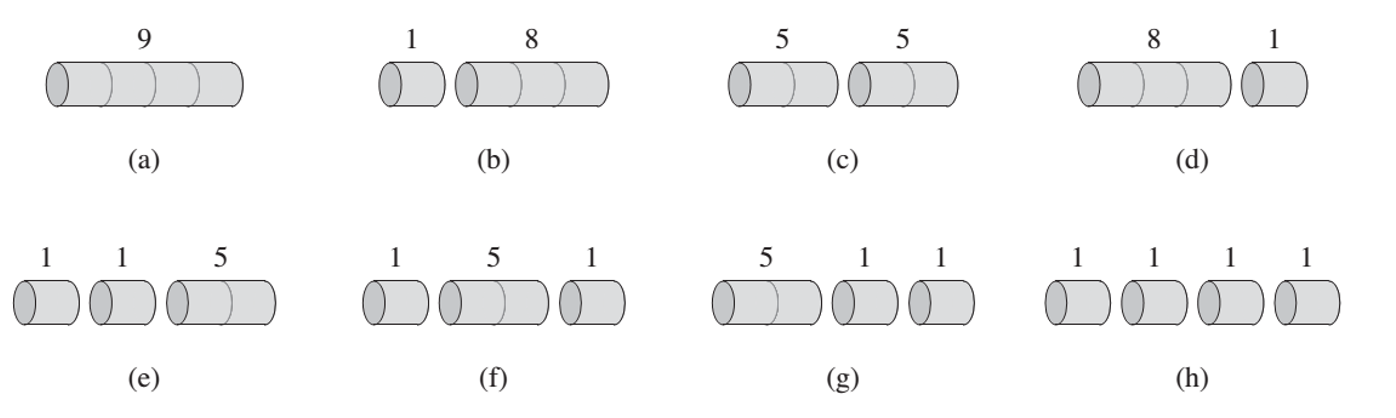
显而易见，对于 4 英寸的钢条来说，\(c\) 切割法收益最大。

自顶向下递归

问题分解为：将长度为 \(n\) 的钢条分解为左边一段，以及剩余部分需要继续分解的一段。

\[r_n=max(p_i+r_{n-i}),1\leq{i}\leq{n} \]

int cutRod(int[] p, int n) {
	if(n == 0) return 0;
  int q = -inf;
  for(int i = 1; i <= n; i++) {
  	q = max(q, p[i]+cutRod(p, n-i));
  }
  return q;
}

但是该方法效率十分差，因为它会反复地用相同的参数值对自身进行递归调用。

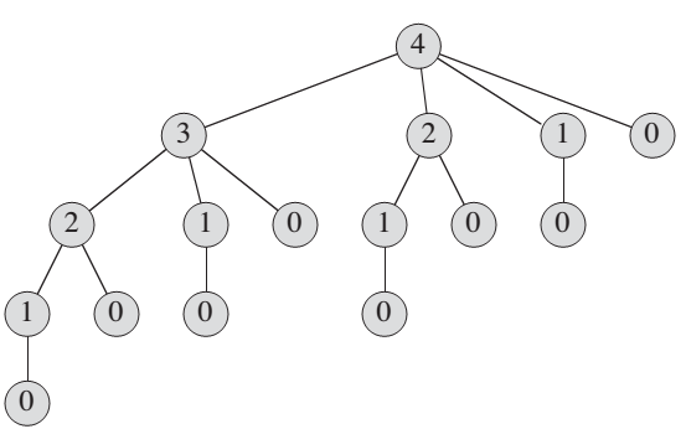
带备忘的自顶向下

自顶向下的过程中，会保存每个子问题的解（数组或者散列表）。当需要一个子问题的解时，首先检查是否已经保存过此解。

int memorizedCutRod(int[] p, int n, int[] r) {
	if(r[n] >= 0) return r[n];
  if(n == 0) return 0;
  else {
    int q = -inf;
    for(int i = 1; i <= n; i++) {
      q = max(q, p[i]+memorizedCutRod(p, n-i, r));
    }
  }
  r[n] = q;
  return q;
}

自底向上

将子问题按规模排序，按由小到大的顺序进行求解。当求解某个子问题时，它所依赖的哪些更小的子问题都已求解完毕，结果已经保存。每个子问题只需求解一次，当我们求解它时，它的所有前提子问题都已求解完成。

int bottomUpCutRod(int[] p, int n) {
	int[] r;
  r[0] = 0;
  for(int i = 1; i <= n; i++) {
  	int q = -inf;
    for(int j = 1; j <= i; j++) {
    	q = max(q, p[i] + r[j-i]);
    }
    r[i] = q;
  }
  return r[n];
}

最长公共子序列（LCS）

问题描述

输入：\(X=(x_1,x_2,x_3,...,x_m)\)，\(Y=(y_1,y_2,y_3,...,y_n)\)

输出：\(Z\) 是 \(X\) 和 \(Y\) 最长公共子序列

LCS 最优解结构特征

定义 \(X\) 的 \(i^{th}\) 前缀：\(X_i=(x_1,x_2,...,x_i)\)

设序列 \(X=(x_1,x_2,x_3,...,x_m)\) 和 \(Y=(y_1,y_2,y_3,...,y_n)\)，\(Z=(z_1,z_2,...,z_k)\) 是 \(X\) 和 \(Y\) 的任意一个 LCS，则

• 若 \(x_m=y_n\Longrightarrow{z_k=x_m=y_n}\)，且 \(Z_{k-1}\) 是 \(X_{m-1}\) 和 \(Y_{n-1}\) 的一个 LCS
• 若 \(x_m\neq{y_n},z_k\neq{x_m}\Longrightarrow{Z}\) 是 \(X_{m-1}\) 和 \(Y\) 的一个 LCS
• 若 \(x_m\neq{y_n},z_k\neq{y_n}\Longrightarrow{Z}\) 是 \(X\) 和 \(Y_{n-1}\) 的一个 LCS

子问题的递归解

\(c[i,j]\) 表示 \(X_i\) 和 \(Y_j\) 的 LCS 长度

\[c[i,j]= \begin{cases} 0 & i=0或j=0 \\ c[i-1,j-1]+1 & i,j>0,x_i=y_j \\ max\left\{c[i,j-1],c[i-1,j]\right\} & i,j>0,x_i\neq{y_j} \end{cases} \]

计算最优解值

\(b[i,j]\) 存放构造最优解的信息

\[b[i,j]= \begin{cases} \nwarrow & c[i,j]由c[i-1,j-1]确定 \\ \uparrow & c[i,j]由c[i-1,j]确定\\ \leftarrow & c[i,j]由c[i,j-1]确定 \end{cases} \]

当构造解时，从 \(b[m,n]\) 出发，上溯至 \(i=0\) 或 \(j=0\) 为止，在上溯过程中，当 \(b[i,j]\) 遇到 \(\nwarrow\) 时，打印 \(x_i,y_j\)

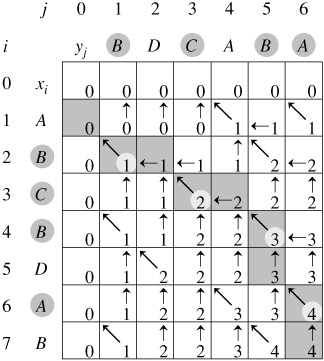
void LCS(String X, String Y) {
	int m = length(X);
  int n = length(Y);
  for(int i = 0; i <= m; i++) c[i][0] = 0;
  for(int j = 0; j <= n; j++) c[0][j] = 0;
  for(int i = 1; i <= m; i++) {
  	for(int j = 1; j <= n; j++) {
    	if(X[i] == Y[j]) {
      	c[i][j] = c[i-1][j-1]+1;
        b[i][j] = "1";
      }
      else if(c[i-1][j] >= c[i][j-1]) {
      	c[i][j] = c[i-1][j];
        b[i][j] = "2";
      }
      else {
      	c[i][j] = c[i][j-1];
        b[i][j] = "3";
      }
    }
  }
}

时间 \(O(mn)\)

构造一个 LCS

void printLCS(char[][] b, String X, int i, int j) {
	if(i == 0 || j == 0) return;
  if(b[i][j] == '1') {
  	printLCS(b, X, i-1, j-1);
    print(X[i]);
  }
  else {
  	if(b[i][j] == '2') printLCS(b, X, i-1, j);
    else printLCS(b, X, i, j-1);
  }
}

时间 \(O(m+n)\)