超导电路｜课本学习笔记｜第3章约瑟夫森效应

第3章约瑟夫森效应

3.1 单电子隧道效应

当两块金属被一个薄的绝缘体分开时，在它们之间可能有电流流过，称金属-绝缘体-金属 (N-I-N) 叠层为隧道结，隧道结中流动的电流为隧道电流。

根据结两端物质的不同可将其分为正常金属隧道、超导体与正常金属之间的隧道和超导体隧道。

1. 正常金属隧道效应

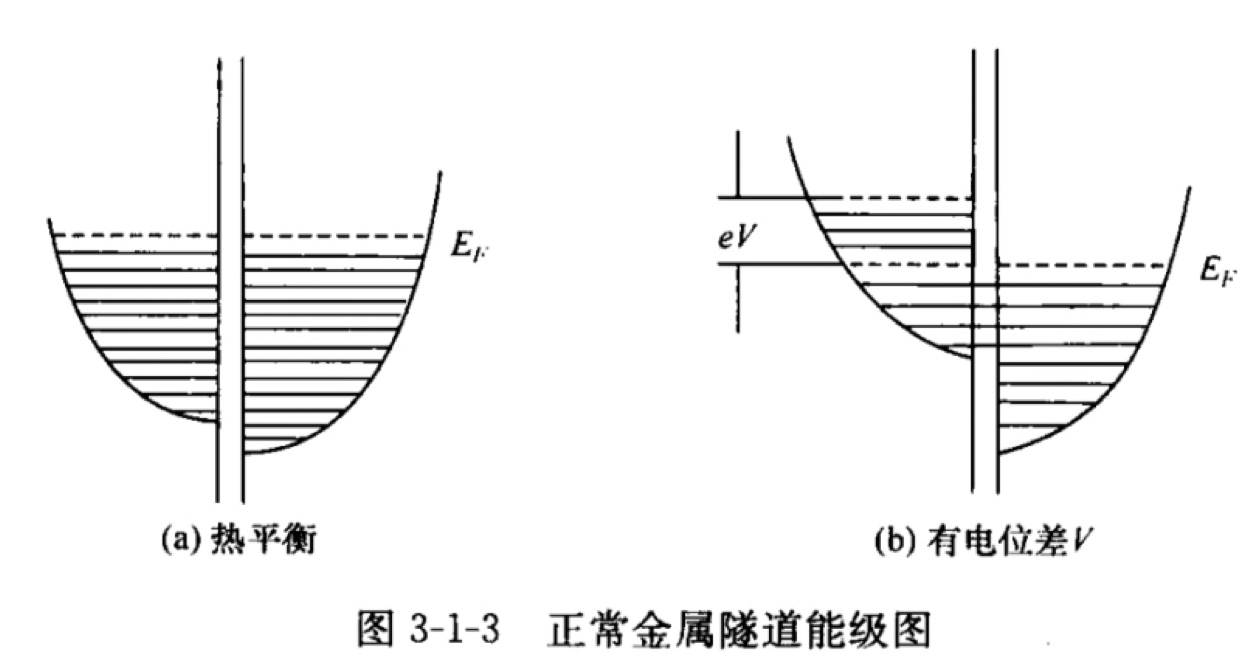
在 T=0K 时有一个 N-I-N 结，在热平衡时有两个金属的费米能是相同的，隧道中没有隧道电流
在隧道结上施加电压 V，左侧所有电子的能量提高 eV，产生隧道电流。

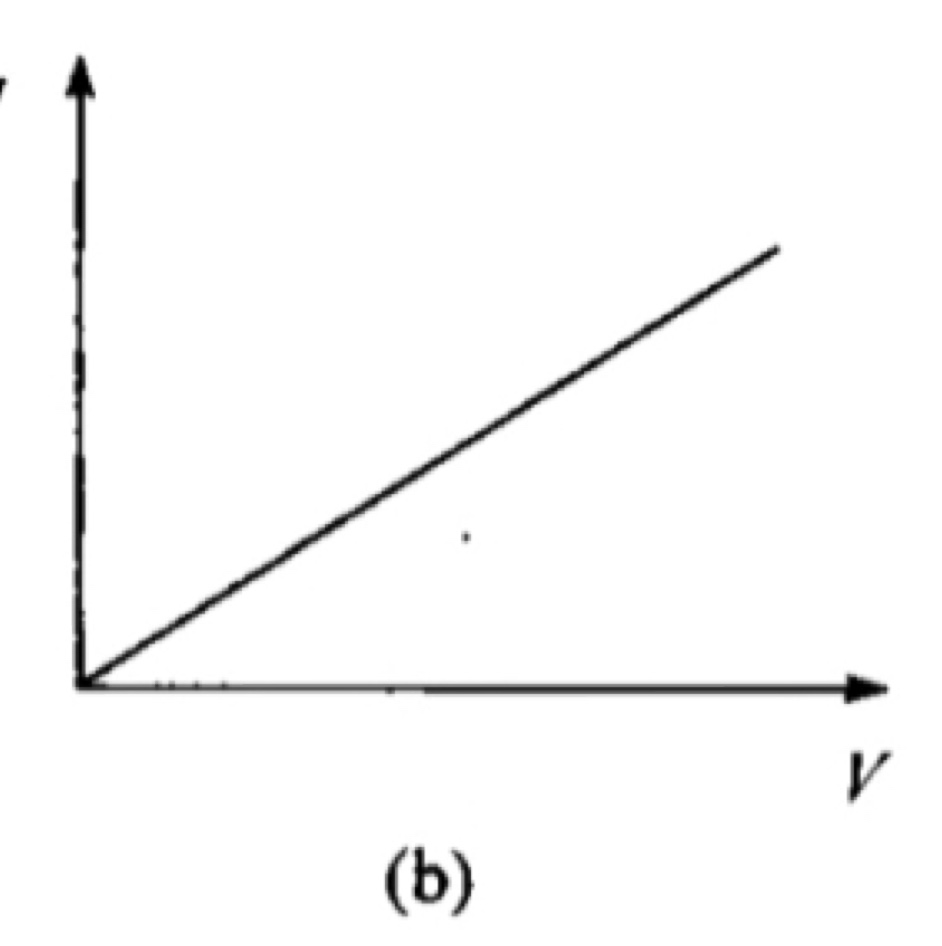
当结的偏置电压较小时，隧道电流 I 与结电压 V 呈线性关系

\[I=\sigma_{N} V=\frac{1}{R_{N}} V \]

\(R_N\) 称为 N-I-N 隧道结的正常电阻

2. 超导体和正常金属间隧道效应（金属-绝缘体-超导体 (N-I-S) 结）

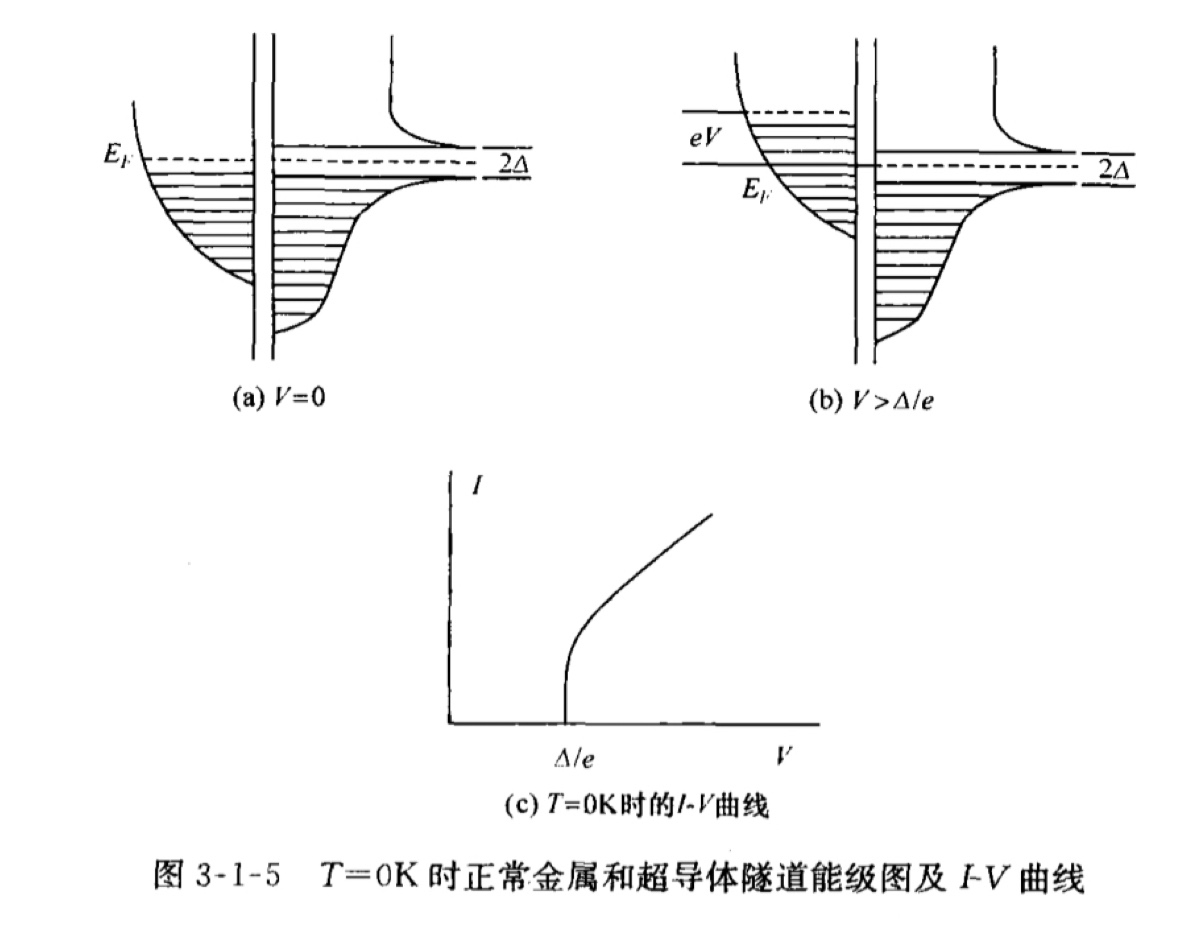
(T=0K时)
1. 热平衡时，结两边材料的费米能必须相等，此时隧道中不产生电流； (a)
2. 当施加电压 V<∆/e 时，不产生隧道电流；
3. 当施加电压 V=∆/e 时，左侧金属费米能级的电子与右侧超导体能隙上边缘的无态密度的空穴对齐，开始产生隧道电流，随 V 的微弱增大而急剧增大；(b)
4. 当 V>∆/e 时，电子对应能量右边的态密度减小，因此电流随电压的增加反而较缓地增加。
5. I-V特性如图。 (c)

（当0<T<Tc）
1. 热平衡时不产生电流；(a)
2. 当施加电压 V<∆/e 时，左侧金属在费米能级以上的电子开始流向右侧超导体能隙以上的空穴，因此一个很小的电压可以产生电流；
3. 当施加电压 V=∆/e 时，电流在此附近才会迅速增加；
4. 电压继续增大，隧道电流与偏置电压趋于线性关系。
5. I-V特性如图。(b)

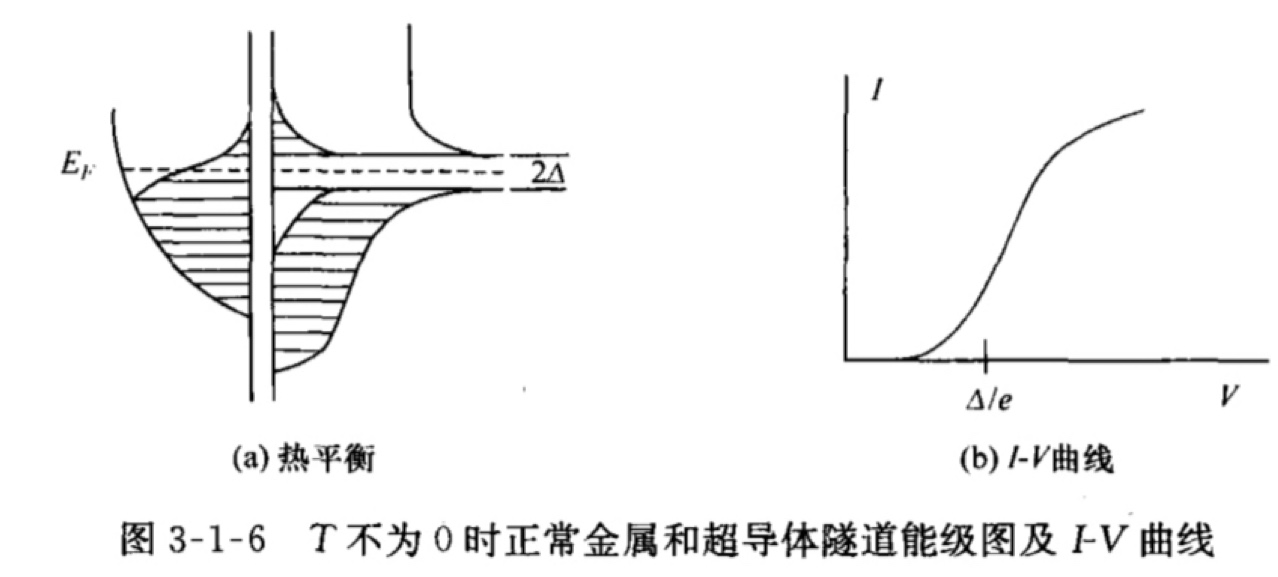
PS：改变偏置的极性，上图的 I-V 特性曲线保持不变，超导隧道结与半导体PN结在此处不同

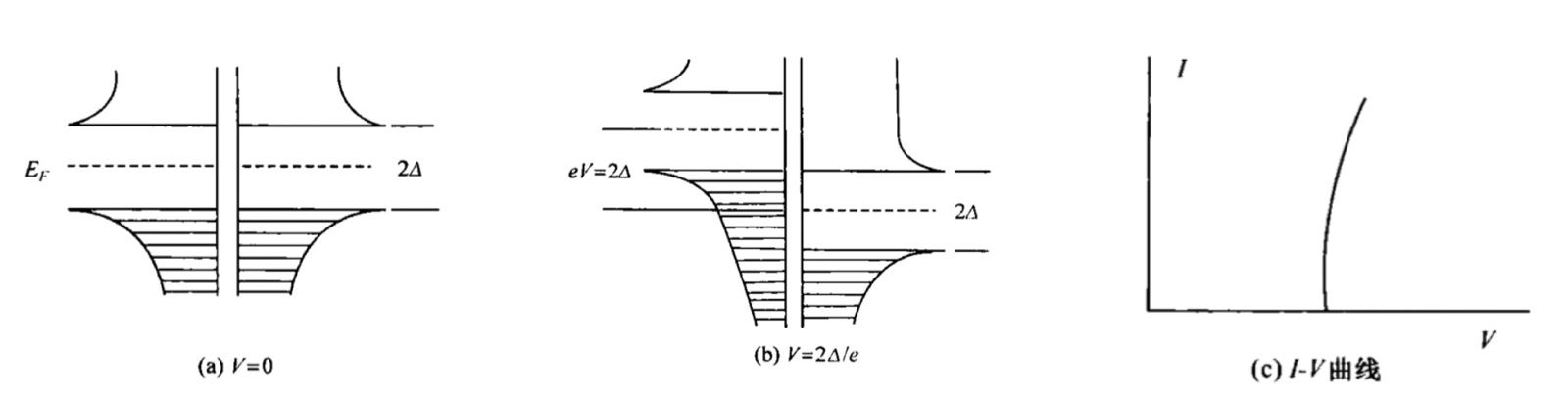
3. 超导体单电子隧道效应（S-I-S结）

结两边是相同超导体的 S-I-S 结，且T=0K
1. 两侧超导体中电子能级都在能隙以下，在热平衡时没有电流产生； (a)
2. 当施加电压 V<2∆/e 时，左侧能隙下方电子到右侧没有可占据的空穴，因此无电流产生；
3. 当施加电压 V=2∆/e 时，左侧能隙下方电子在右侧能隙上方获得可占据的空穴，电流突然增大; (b)
4. I-V特性如图 (c)

结两边为不同能隙（∆1和∆2）的超导体的情况，即 S1-I-S2 结

（T=0K时）
1. 当 V>=(∆1+∆2)/e 时才开始产生隧道电流

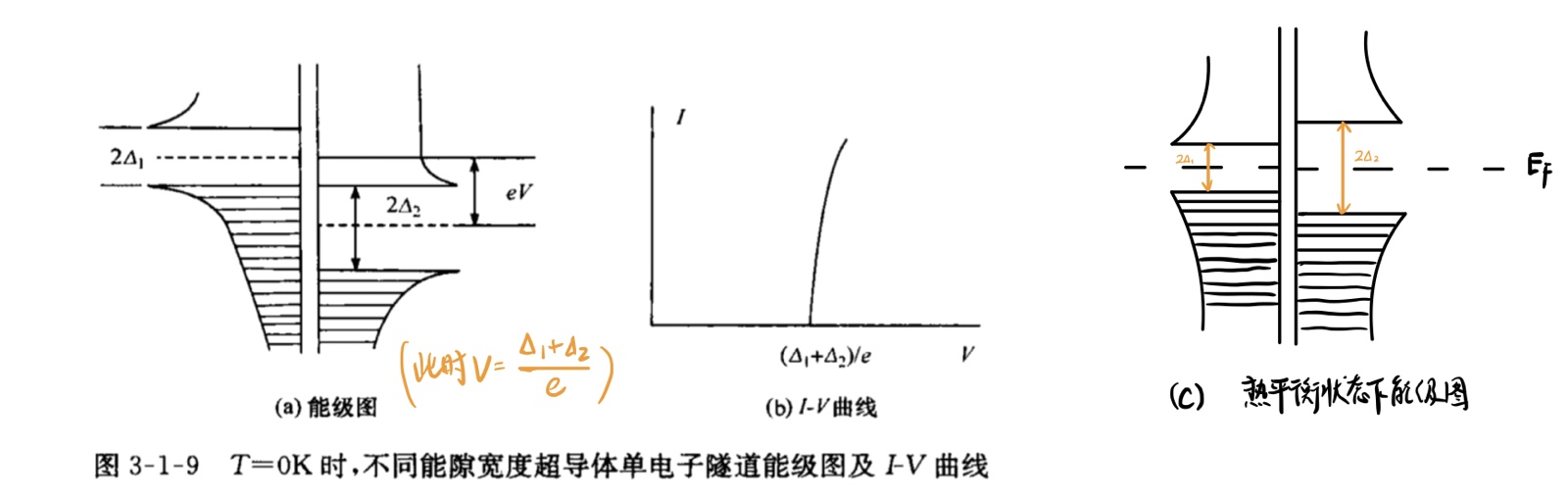
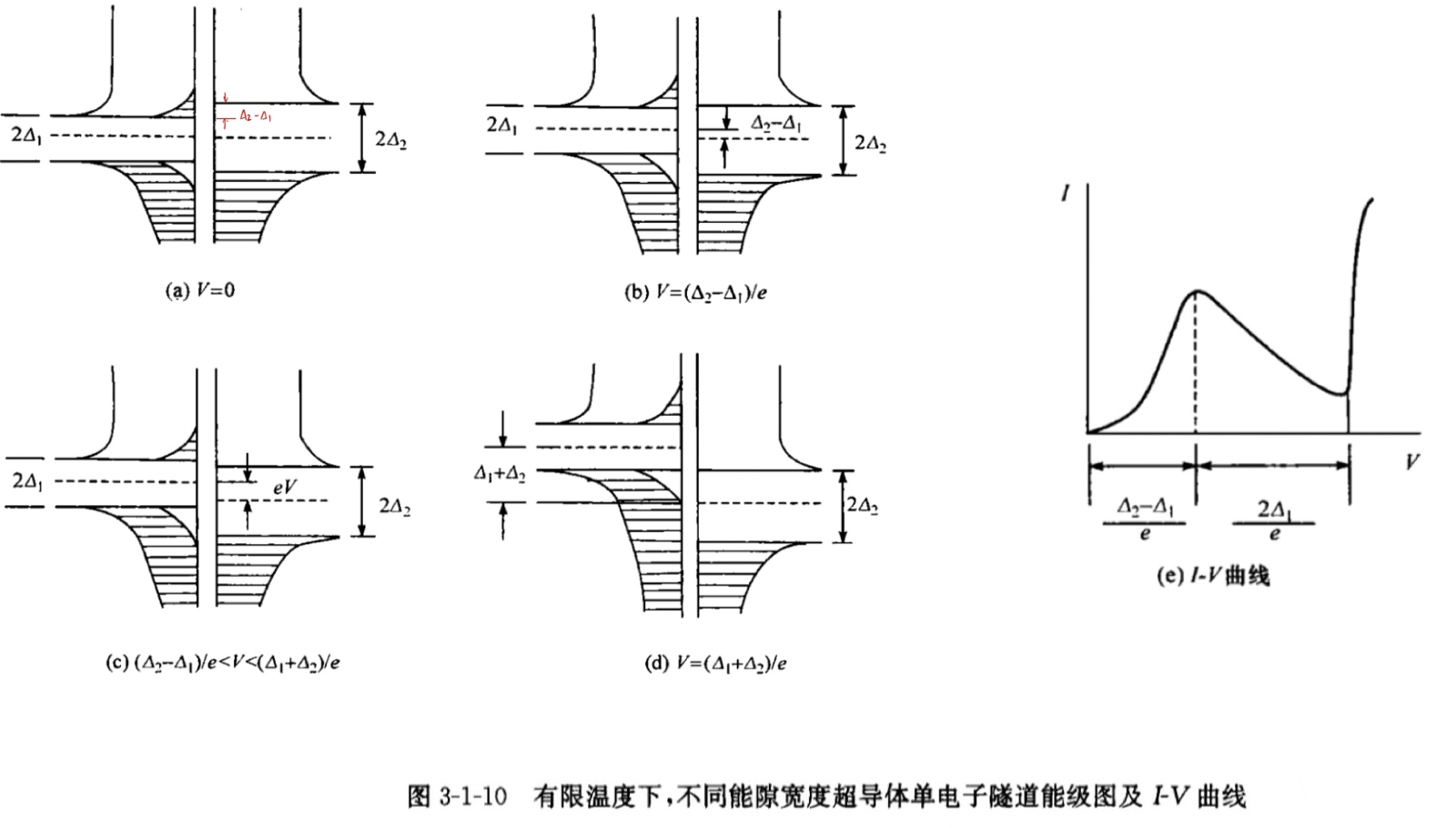
（当 \(T_{c1}<T<T_{c2}\)时）
1. 热平衡时，类似NIS结的有限温度的讨论，S1-I-S2结两端一旦加上电压就会有隧道电流产生； (a)
2. 当施加电压 V=(∆2-∆1)/e 时，与左侧超导体能隙以上的热激发电子的能量相对应的右侧超导体具有较大的空穴密度，因此此时的隧道电流达最大值。； (b)
3. 当施加电压 V=(∆2-∆1)/e<V<(∆2+∆1)/e 时，左侧超导体能隙上方的电子对应的是右侧超导体能隙上方较小的态密度，因此电流持续减小并出现负阻的情况。 (c)
4. 当施加电压 V=(∆2+∆1)/e 左侧超导体能隙下边缘的电子获得右侧超导体能隙上边缘密度无限大的空穴，电流急剧增大； (d)
5. I-V特性如图。 (e)

3.2 约瑟夫森理论

约瑟夫森方程

\[\begin{array}{c} J_{s}=J_{c} \sin \Delta \varphi \\ \frac{\partial(\Delta \varphi)}{\partial t}=\frac{2 e V_{0}}{\hbar} \\ \frac{\partial(\Delta \varphi)}{\partial x}=\frac{2 e \Lambda}{\hbar} B_{y} \\ \frac{\partial(\Delta \varphi)}{\partial y}=\frac{2 e \Lambda}{\hbar} B_{x} \end{array} \]

\(J_s\) 表示隧道结超导电流密度， \(J_c\) 表示隧道结的临界电流密度， \(V_0\) 表示结两端电压， \(\Delta \varphi\) 表示波函数的位相角 \(\varphi_1\) 和 \(\varphi_2\) 的差， \(\Lambda\) 表示磁场宽度

直流约瑟夫森效应
- 内容：存在一个超导电流，超导电流的大小由结两端电子对波的相位差决定。
- 过程：
  1. 直流超导电流穿过隧道结，只要电流不大于临界电流，隧道结呈现无阻的性质，从而结两端电压为零，其伏安特性曲线是Y轴（电流轴）的一段直线； (a)
  2. 如果电流继续增加且超过临界电流Ic，那么无阻特性被破坏，直流约瑟夫森效应消失，但是单电子隧道效应仍进行，显示出隧道结两端电压不为零即结电阻不等于零； (b)
  3. 如果电源电阻比结电阻大很多，结电阻对出现对电路电流的影响较小，可以把电源看成恒流源：
    从直流约瑟夫森效应曲线到单电子隧道效应曲线到转换是按上面的水平虚线 (c) 进行，反之由于隧道结电容的存在，相反方向的转换是按下面的水平虚线 (d) 进行（此现象称为迟滞）。

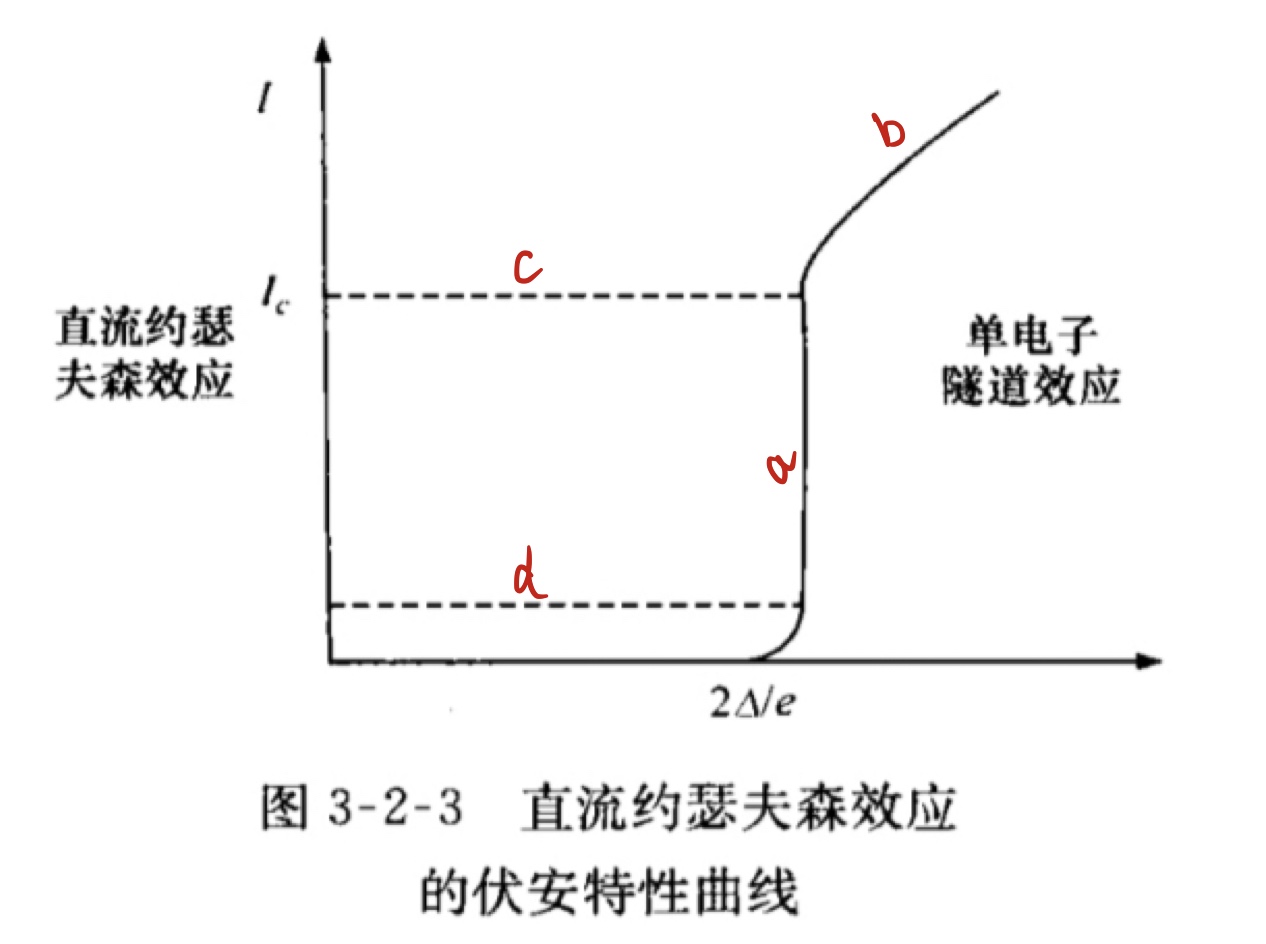
PS：对于结来说，当电流超过临界电流之后，一方面有正常电子运载的有阻电流通过，同时还有交变的超导电流通过（均值为零看不出来），此时的绝缘薄层处于电阻-超导状态。

交流约瑟夫森效应
- 内容：交变超导电流的变化频率（称为约瑟夫森频率）与隧道结两端的电压成正比。
- 过程:
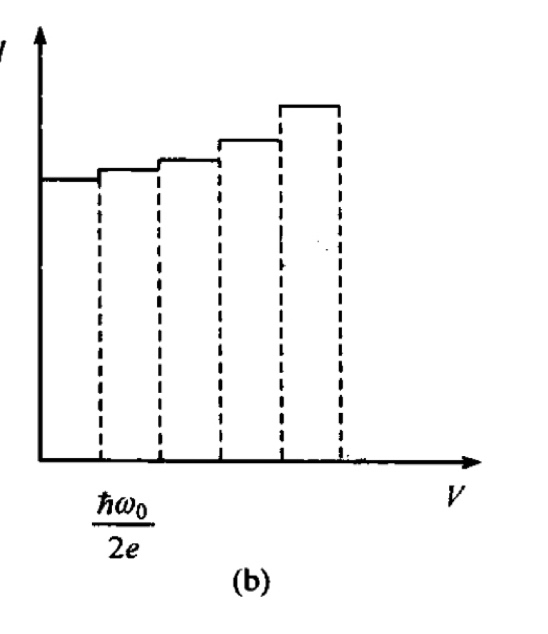
  在证明交变超导电流的存在的过程中, 得到 \(V_{n}=\frac{n \hbar \omega^{\prime}}{2e}\) 处有直流小峰（直流成分的超导电流) 因此在满足上述条件的 \(V_n\) 处，出现一系列的电流“台阶” (称为微波感应台阶)。

3.3 约瑟夫森结的典型结构及其等效电路

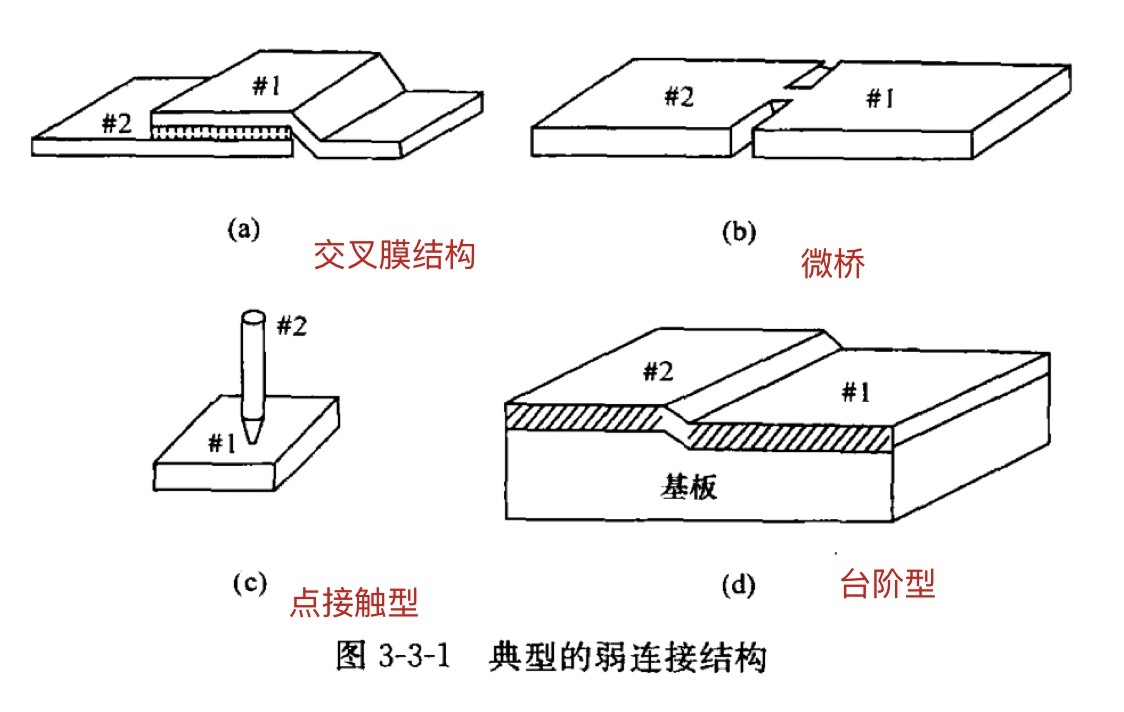
约瑟夫森的典型结构
一般来说，约瑟夫森结的形成是由于两个超导体之间实现了弱连接

斯图尔特-麦克坎伯模型

实际上，约瑟夫森结中除了有超导电流之外，还有正常电流通过，因此要考虑超导隧道结的常态电阻 \(Rn\) ，此外由于电压和电流随时间变化，因此需要考虑超导隧道结的电容和电感。

在约瑟夫森结中有无阻的超导电流 \(I_s\) 、有阻的超导电流 \(I_n\) 和电容器中的位移电流 \(I_d\) ，总电流为三者之和。

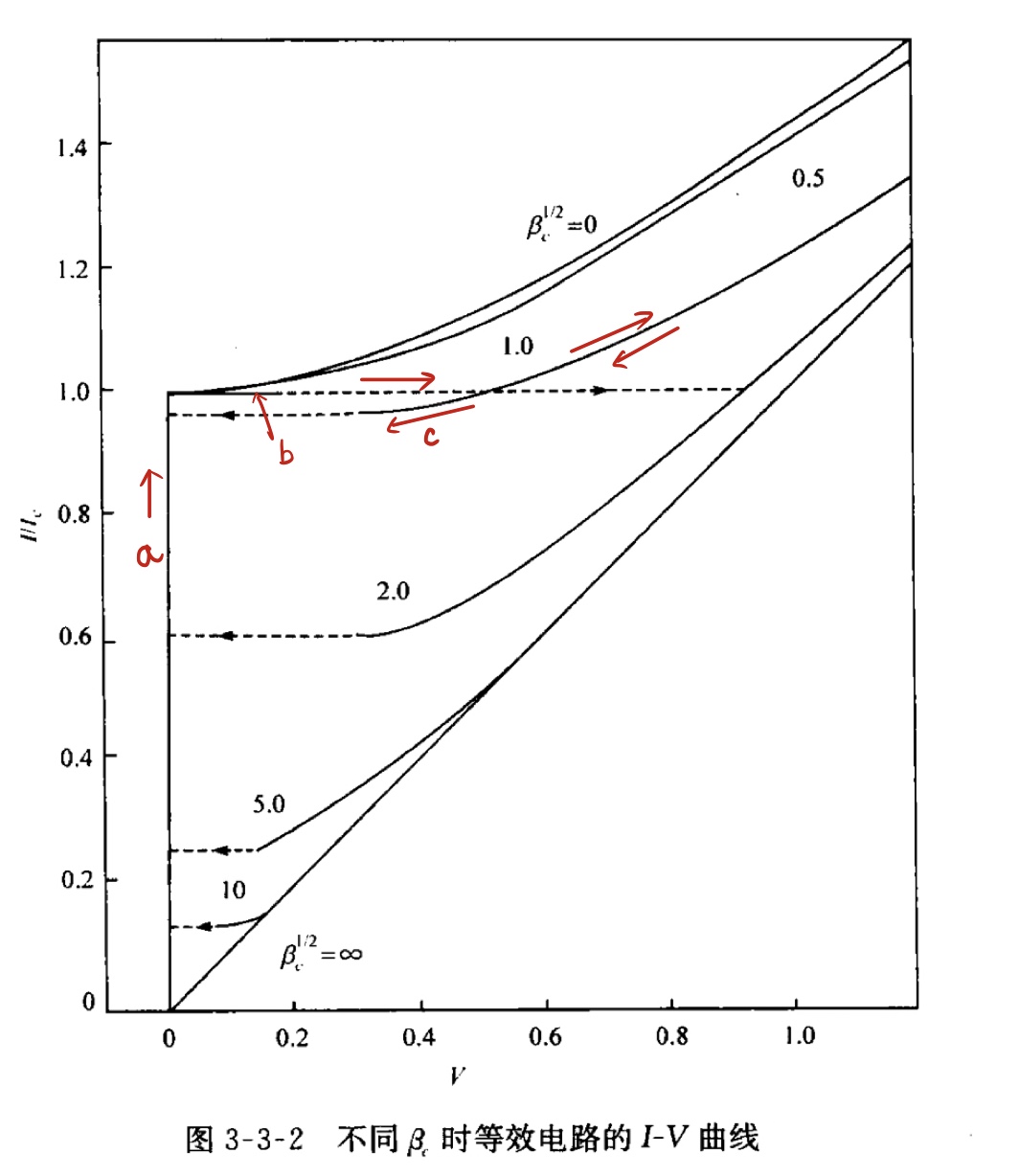
在不同 \(\beta \mathrm{c}\) 时等效电路的 \(1-V\) 特性

（实线部分表示可逆变化, 虚线部分表示不连续的跳跃变化，箭头表示跳跃方向）（以 \(\beta c=1\) 为例, \(a, b, c\) 画线不一定正确）

当电容不能忽略时, 即 \(\beta c>1\) 时, 结属于欠阻尼状态, 此时的 \(I-V\) 特性出现回滞, 在 \(I\) 增加到 \(I_c\) 之前, \(V=0\) (a); 在 \(I=I_c\) 时, 突然出现电压 \(V_g=2 \Delta /e\) (b);

如果电流从 \(I_c\) 开始下降, 电压并不回零, 而是到 \(I=I_{ro}=\frac{4I_{c}}{\pi Q}\) 时, 电压才跳变为零 \((c)\) 。

斯图尔特-麦克坎伯等效电路

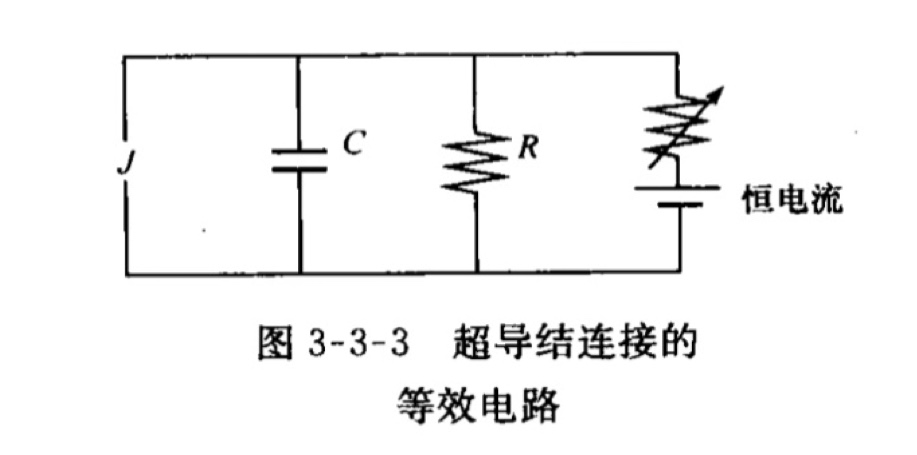
J是理想约瑟夫森结，其电阻和电容为零

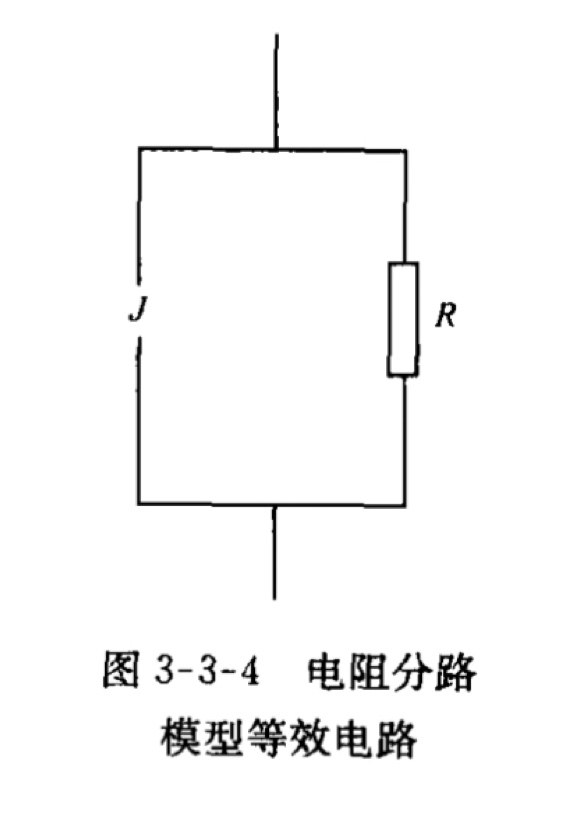
电阻分路模型

对于超导微桥、超导点接触和小尺寸的隧道结，它们的电容很小可忽略，此时与理想约瑟夫森结并联的是一定数值的电阻，称为电阻分路结模型（ RSJ 模型）。

3.4 约瑟夫森结的起伏噪声（略）

3.5 实用约瑟夫森结的特性（略）

posted @ 2022-07-29 20:51 一抹微瀾阅读(1773) 评论(0) 收藏举报

刷新页面返回顶部

超导电路｜课本学习笔记｜第3章 约瑟夫森效应

第3章 约瑟夫森效应