福利👴变换公式

本文抄了抄课件，摆放了一下课件给的公式。

好难啊……再懂一点再补了

前情提要

欧拉公式（Euler's Formula）

\[e^{i\theta} = \cos(\theta) + i\sin(\theta) \]

余弦函数的指数形式

\[\cos(\theta) = \frac{e^{i\theta} + e^{-i\theta}}{2} \]

正弦函数的指数形式

\[\sin(\theta) = \frac{e^{i\theta} - e^{-i\theta}}{2i} \]

特征函数

定义：类比线性代数里的特征向量。

\[\phi_k(t) \quad \longrightarrow \quad \boxed{\text{LTI}} \quad \longrightarrow \quad \lambda_k \phi_k(t) \]

比如 \(\delta(t)\) 的特征函数是任何函数，\(\delta(t-T)\) 的特征函数是以 \(T\) 为周期的函数。

根据 LTI 的叠加原理，如果能把输出信号表示成一系列特征函数的和，就能很容易地求出输出信号：

\[x(t) = \sum_k a_k \phi_k(t) \quad \longrightarrow \quad \boxed{\text{LTI}} \quad \longrightarrow \quad y(t) = \sum_k \lambda_k a_k \phi_k(t) \]

太好了，但是怎么分解呢？

\(e^{st}\)

• 于是有人发现几乎任何 \(e^{st}\) 经过任何 LTI 结果都还是自己的倍数。（其中 \(s\) 是复数）

证明：\(x(t)=e^{st}\)，那么有：

\[y(t) = x(t) * h(t) = \int_{-\infty}^{+\infty} h(\tau) x(t-\tau) d\tau \\ = \int_{-\infty}^{+\infty} h(\tau) e^{s(t-\tau)} d\tau \\ = \left[ \int_{-\infty}^{+\infty} h(\tau) e^{-s\tau} d\tau \right] e^{st} \\ = H(s) e^{st} \]

（通过这个证明可以发现其实 \(2^{st}\) 之类的指数函数也是特征函数，只不过 \(2^{st}\) 其实就是 \(e^{st}\) 把 \(t\) 缩放 \(\ln 2\) 倍，而 \(e\) 具有更好的性质）

好，那我们就决定用 \(e^{st}\) 当特征函数了，而且只要 \(s\) 固定，不管什么系统都可以直接知道特征值：

\[H(s)=\int_{-\infty}^{+\infty} h(\tau) e^{-s\tau} d\tau \]

（这个公式其实是对 \(h\) 做拉普拉斯变换，不过我还没学，后面看到了傅里叶变换你会发现跟这个很像）

那现在的首要任务是把 \(x(t)\) 分解成 \(\sum a_k e^{s_k t}\) 的形式。

• 于是又有人发现几乎任何信号都可以分解为若干个 \(e^{st}\) 的线性组合。（至少自然界中常用的信号都能）

而且即使 \(s\) 是纯虚数也暂时够用，那接下来的内容我们默认 \(s\) 是纯虚数，也就是 \(e^{j\omega t}\) 的形式。

（其实傅里叶变换是拉普拉斯变换在纯虚数情况下的特例）

指数傅里叶级数

傅里叶定理：任何周期函数都可以表示为复指数函数的无限和。

也就是我们直接开拆，假设能这么分解：

\[x(t)=\sum\limits_{k=-\infty}^{+\infty}c_ke^{jk\omega_0t} \]

其中 \(\omega_0=\frac{2\pi}T\)，毕竟是给周期函数分解嘛，分解出的函数肯定都有个基频的。

傅里叶给出了 \(c_k\) 公式：

\[c_k=\frac 1 T \int_0^T x(t)e^{-jk\omega_0 t}dt \]

这是因为，分解之后的任意两个不同频率的基函数是正交的（如何计算正交：\(\int f(x)g^{*}(x)dx\)，其中 \(g^{*}\) 为 \(g\) 的共轭），也就是：

\[\frac{1}{T}\int_0^T e^{jm\omega_0 t} e^{-jn\omega_0 t} dt = \frac{1}{T}\int_0^T e^{j(m-n)\omega_0 t} dt = \begin{cases} 1 & m = n \\ 0 & m \neq n \end{cases} \]

就好比三维空间中的向量投影到 \(x\) 轴上，\(y\) 和 \(z\) 分量就都会归零一样。我们让 \(f(x)\) 点乘 \(e^{jk\omega_0t}\)，就相当于 \(f(x)\) 这个大函数投影到 \(k\) 这一维，就可以把其它分量都归零，只留下这个基函数的系数。这就是 \(c_k\) 的来源。

至此，你已经可以自己分解了。

举个栗子：分解梳子函数

\[comb(t)=\sum\limits_{m=-\infty}^{+\infty}\delta(t-mT) \]

计算 \(\omega_0=\frac{2\pi}{T}\)

分解形状 \(x(t)=\sum\limits_{k=-\infty}^{+\infty}c_ke^{jk\omega_0t}\)

计算 \(c_k =\frac 1 T\int_0^T x(t)e^{-jk\omega_0t}dt=\frac 1 T\int_0^T\left( \sum\limits_{m=-\infty}^{+\infty}\delta(t-mT) \right) e^{-jk\omega_0t}dt\)

注意 \(t\) 的取值范围只有 \([0,T)\)，因此其实只有 \(m=0,t=0\) 时才可能出现 \(\delta(t-mT)=1\)，此时算出 \(c_k=\frac 1 T\)。

所以 \(comb(t)=\sum\limits_{k=-\infty}^{+\infty}\frac 1 T e^{jk\frac{2\pi}{T}t}=\frac 1 T \sum\limits_{k=-\infty}^{+\infty} e^{jk\frac{2\pi}{T}t}\)

地理课雷条件

顺便提一嘴，前面说几乎任何信号都能用傅里叶级数分解，那么具体是什么样的信号才能被这样分解呢？

1. \(x(t)\) 在一个周期内绝对可积，即：

\[\int_T |x(t)|dt<\infty \]

2. 在有限的时间区间内，函数 \(x(t)\) 有有限个极大值和极小值。

3. 在有限的时间区间内，函数 \(x(t)\) 只有有限个不连续点。

否则，傅里叶级数就无法收敛到原函数。

三角傅里叶级数

欧拉公式：

\[e^{j\theta}=\cos\theta+j\sin\theta \]

我们欧拉公式可以把复指数函数转化成三角函数，也就是说，一个信号也能表示成若干个 \(\sin\) 和 \(\cos\)。

我们知道每个函数都可以拆成一个奇函数和偶函数，刚好 \(\sin\) 负责奇部，\(\cos\) 负责偶部，然而 \(\sin\) 和 \(\cos\) 的平均值都是 \(0\)，所以肯定凑不出来，需要再加一个常数凑平均值：

\[f(t)=a_{0}+\sum_{n=1}^{\infty}\Bigl[a_{n}\cos(n\omega_{0}t )+b_{n}\sin(n\omega_{0}t)\Bigr]\]

\(\sin n\omega_0t\) 或 \(\cos n\omega_0 t\) 统称第 n 次谐波，n 为奇数叫奇次谐波，n 为偶数叫偶次谐波，\(a_n\)，\(b_n\) 为傅里叶系数。

傅里叶分析

所以我们怎么确定 \(a_0\)，\(a_n\)，\(b_n\)？

\[f(t)=a_{0}+\sum_{n=1}^{\infty}\Bigl[a_{n}\cos(n\omega_{0}t) +b_{n}\sin(n\omega_{0}t)\Bigr]\]

和前面的指数函数一样，三角函数也具有正交性。那么我们也用原函数和三角函数点乘来得到每一维的系数。

最后的结论是：

\[a_n = \frac{2}{T} \int_0^T f(t) \cos n\omega_0 t \, dt \]

\[b_n = \frac{2}{T} \int_0^T f(t) \sin n\omega_0 t \, dt \]

最后还有平均值 \(a_0\)：

\[a_0=\frac 1 T\int_0^T f(t) dt \]

运用我们高中学到的三角函数知识，第 \(n\) 次谐波虽然分为 \(\cos\) 和 \(\sin\)，但是它们频率相同，所以是可以合成一个单一余弦波的（只不过多了相位）。

\[f(t)=a_0+\sum\limits_{n=1}^{\infty}A_n\cos(n\omega_0t+\phi_n) \]

对于这个新的余弦波，可以通过公式计算振幅和相位：

\[A_n=\sqrt{a_n^2+b_n^2} \]

\[\phi_n=-tan^{-1}\frac{b_n}{a_n} \]

哦对了，如果你要分解的函数有跳变，这样软绵绵的波形肯定是没法严格拼出来的，跳变处的值大概是两边值的平均数。

而且吉布斯现象（Gibbs Effect）说到，当你用有限项傅里叶级数去逼近一个含有跳变的周期信号时，在跳变边缘会出现约 \(9\%\) 的“上冲”和阻尼振荡，无论再怎么增加项数，这个 \(9\%\) 的上冲始终存在。（如下图边上这个小尖尖）

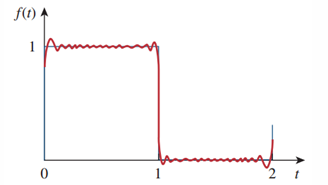
傅里叶级数的性质

如果信号 \(x(t)\) 的傅里叶级数系数为 \(c_k\)：

1. 时间平移（Time shifting）
   \(x(t-t_0)\) 的傅里叶级数系数为 \(e^{-jk\omega_0t_0}c_k\)
2. 共轭（Conjugate）
   \(x*(t)\) 的傅里叶级数系数为 \(c_{-k}^{*}\)
3. 时间反转（Time reversal）
   \(x(-t)\) 的傅里叶级数系数为 \(c_{-k}\)
4. 缩放（Scaling）
   \(x(at)\) 的傅里叶级数系数还是 \(c_k\)，但是频率变为原来的 \(\frac 1 a\)
5. 微分（Differentiation）
   \(x'(t)\) 的傅里叶级数系数为 \(jk\omega_0c_k\)
6. 积分（Integration）
   \(\int_{-\infty}^t x(t)dt\) 的傅里叶级数系数为 \(\left(\frac{1}{jk\omega_0}\right)c_k\)
7. 乘法（Multiplication）
   如果 \(x(t)\) 和 \(y(t)\) 的傅里叶级数系数分别为 \(a_k\) 和 \(b_k\)，那么 \(x(t)y(t)\) 的傅里叶级数系数为 \(\sum\limits_{l=-\infty}^{+\infty}a_lb_{k-l}\)

帕塞瓦尔定理

一个周期信号的平均功率等于其各个谐波的个别功率之和。

用公式表示：

\[\frac{1}{T}\int_{T} |x(t)|^{2}\,dt = \sum_{k=-\infty}^{\infty} |c_{k}|^{2} \]

为什么左边是完整信号，右边只有系数呢？

因为

\[\frac{1}{T}\int_{T} \bigl|\mathrm{e}^{\mathrm{j}k\omega_{0}t}\bigr|^{2}\,dt = 1 \]

那么离散信号呢

首先来回顾一下信号的周期性。

还是设信号为 \(e^{j\omega_0 n}\)。的，\(\omega_0=\frac{2\pi}n\) 在复平面上仍然表示经典角速度。

要找到信号的周期 \(N\) 也就是 \(e^{j\omega_0 n} = e^{j\omega_0 (n+N)} = e^{j\omega_0 n}e^{j\omega_0 N}\)，需要 \(e^{j\omega_0 N}=1\)，也就是 \(\omega_0 N\) 带着它转若干周（假设 \(m\) 周），\(\omega_0 N = 2\pi m\)。由于 \(N\) 和 \(m\) 都没确定，\(\omega_0 = \frac{2\pi m}{N}\)，即 \(\omega_0\) 必须是 \(\pi\) 的实数倍。

如果想找到最小周期，\(\frac N m=\frac{2\pi}{\omega_0}\)，化成最简分数即可。

由于是 DT，频率越高不一定点越密集，因为有可能点绕了很多圈又回去了，有 \(e^{j\omega_0 n}=e^{j(\omega_0+2\pi)n}\)，最密 \(e^{j\pi n}=(-1)^n\)，最疏 \(e^0=1\)

谐波

\(e^{j\omega_0 n}\) 是基波，那么 \(e^{jk\omega_0 n}~(k=0,1,\dots,N)\) 是谐波，我们用 \(ψ\) 来存储所有谐波，然而我们刚才说了 \(e^{j\omega_0 n} = e^{j\omega_0 (n+N)\)，其实 \(ψ\) 只存储 \(N\) 个就够了。

\[ψ_k[n]=e^{jk\omega_0 n}~(k=0,1,\dots,N-1) \]

离散信号的傅里叶级数

我们仍然希望把信号拆分成多个谐波！

\[x[n] = \sum_{k=\langle N \rangle} a_k e^{jk\omega_0 n} \]

这一次，所有离散时间周期信号都能这样拆吗？

答案是肯定的！因为值的个数是有限的，所以傅里叶级数是一个有限项的线性组合，不存在收敛性问题。

那么问题就只剩下怎么求系数了，同样利用复指数信号的正交性，把信号 \(x[n]\) 跟每个谐波做内积。

\[a_k = \frac{1}{N} \sum_{n=\langle N \rangle} x[n]\,e^{-jk\frac{2\pi}{N}n} \]

这个系数 \(a_k\) 通常被称为 \(x[n]\) 的频谱系数（spectral coefficients）。可想而知，同样有 \(a_{k+N}=a_k\)。

和连续信号比一下呢：

\[c_k=\frac 1 T \int_0^T x(t)e^{-jk\omega_0 t}dt \]

一些性质

性质类别	时域信号 \(x[n]\)（周期为 \(N\)）	频域系数 \(a_k\) 或对应关系	关键条件/备注
线性性	$ A x[n]+B y[n]$	$ A a_{k}+B b_{k}$	任意周期信号
时移	$ x\left[n-n_{0}\right]$	$ a_{k},e^{-j k \frac{2\pi}{N} n_{0}}$	\(n_0\) 整数
频移	$ x[n],e^{j k_{0} \frac{2\pi}{N} n}$	$ a_{k-k_{0}}$	\(k_0\) 整数
时间反转	$ x[-n]$	$ a_{-k}$
一阶差分	$ x[n]-x[n-1]$	$ \left(1-e^{-j k \frac{2\pi}{N}}\right) a_{k}$
运行和	$ \displaystyle\sum_{m=-\infty}^{n} x[m]$	$ \dfrac{1}{1-e^{-j k \frac{2\pi}{N}}},a_{k}$	仅当直流分量 \(a_0=0\)（否则累加无界）
时域乘法	$ x[n],y[n]$	周期卷积：$ \displaystyle\sum_{\ell=\langle N\rangle} a_{\ell},b_{k-\ell}$	\(b_k\) 为 \(y[n]\) 的系数
周期卷积	$ \displaystyle\sum_{r=\langle N\rangle} x[r],y[n-r]$	$ N,a_{k},b_{k}$	卷积长度 \(N\)
实信号共轭对称	$ x[n]\in\mathbb{R}$	$ a_{k}=a_{-k}^{*}$	自动满足
实偶信号	$ x[n]$ 实且偶	$ a_k$ 实且偶：\(a_k=a_{-k}\in\mathbb{R}\)
实奇信号	$ x[n]$ 实且奇	$ a_k$ 纯虚且奇：\(a_k=-a_{-k}\in j\mathbb{R}\)
偶-奇分解	\(x_e[n]=\mathcal{E}\{x[n]\}\)（实偶部分）\(x_o[n]=\mathcal{O}\{x[n]\}\)（实奇部分）	\(\mathrm{Re}\{a_k\}\) \(j\,\mathrm{Im}\{a_k\}\)	仅对实信号成立

特征值

还有最后一步，经过系统的特征值是什么？

对于 DT：

\[z^n \quad \longrightarrow \quad \boxed{\text{LTI}} \quad \longrightarrow \quad H(z)z^n \]

\(z\) 可以是任意复数，不一定像 CT 一样在单位圆上。不过此处有 \(z^n=e^{jk\omega_0 n}\)（表示形式不一样，不要用 DT 的 z 类比 CT 的 s）

前面已经说了 CT 的特征值：

\[H(s)=\int_{-\infty}^{+\infty} h(\tau) e^{-s\tau} d\tau \]

当 \(s=j\omega\) 时：

\[H(j\omega)=\int_{-\infty}^{+\infty} h(t)e^{-j\omega t}dt \]

DT 的特征值是：

\[H(z)=\sum\limits_{n=-\infty}^{+\infty}h[n]z^{-n} \]

当 \(z=e^{j\omega}\) 时：

\[H(e^{j\omega})=\sum\limits_{n=-\infty}^{+\infty}h[n]e^{-j\omega n} \]

嗯，看起来也是一样的

总结一下，CT 变成 DT 就是把 \(t\) 换成 \(n\)，\(T\) 换成 \(N\)，\((-\infty, \infty)\) 换成 \(<N>\)

滤波器

滤波器是系统，增大想要的频率，滤掉不想要的频率。

频率整形滤波器（Frequency-shaping）：把不像正常信号的信号捏成特定的规整形状

频率选择滤波器（Frequency-selective）：直接砍掉一些信号

一阶 RC 低通滤波器

如果是微分方程怎么办？

举个例子，这是一个电路：

\[RC\,\frac{dv_c(t)}{dt} + v_C(t) = v_s(t) \]

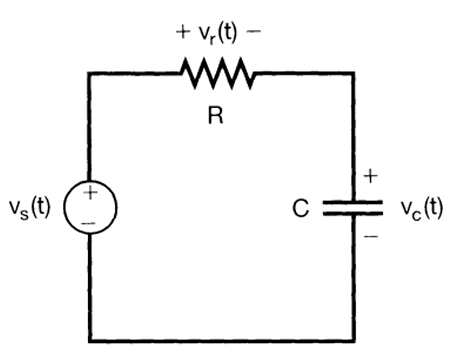
那么 \(v_s\) 相当于输入，\(v_c\) 相当于输出。设 \(v_s(t) = e^{j\omega t}\)，那么一定有 \(v_C(t) = H(j\omega)\,e^{j\omega t}\)（由于我们并没有原函数，所以 \(H\) 还是未知量），并且有 \(\frac{dv_C}{dt} = H(j\omega)\,j\omega e^{j\omega t}\)。

代入微分方程：

\[RC\cdot H(j\omega)j\omega e^{j\omega t} + H(j\omega)e^{j\omega t} = e^{j\omega t} \]

约分得到

\[H(j\omega) = \frac{1}{1 + j\omega RC} \]

解到此处，即使我们不知道原函数，也能通过把 \(x\) 拆分成傅里叶级数，通过 \(H\) 再拼成 \(y\)。

• 幅度：\(\displaystyle |H(j\omega)| = \frac{1}{\sqrt{1 + (\omega RC)^2}}\)
• 相位：\(\displaystyle \angle H(j\omega) = -\arctan\)

从幅度和相位中可以看出系统对不同频率的缩放和延时。（求法：可以用欧拉公式拆成复数，再求模长和幅角）

比如下面这个振幅图，说明它给低频放行的多：

这就是一阶 RC 低通滤波器。

它包含一个电容，因此可以拦住高频，留下低频。

联想一下物理课讲这个电路的时候：

一阶 RC 高通滤波器

还是原来的电路，不再取电容电压，改为取电阻电压。

微分方程：

\[RC\frac{dv_R(t)}{dt} + v_R(t) = RC\frac{dv_s(t)}{dt} \]

用同样的方法解得：

\[G(j\omega) = \frac{j\omega RC}{1 + j\omega RC} \]

拦住低频，留下高频。

一阶递归离散时间滤波器

如果是离散时间呢？

似乎没有微分方程了，只有差分方程。

\[y[n]-ay[n-1]=x[n] \]

不过还是设 \(x[n]=e^{j\omega n}\)，\(y[n]=H(e^{j\omega})e^{j\omega n}\)。

代入：

\[H(e^{j\omega})e^{j\omega n}-aH(e^{j\omega})e^{j\omega (n-1)}=e^{j\omega n} \]

化简得：

\[H(e^{j\omega})=\frac{1}{1-ae^{-j\omega}} \]

非递归离散时间滤波器

\[y[n]=\sum\limits_{k=-N}^{M}b_k x[n-k] \]

是同理的，因题而异。

离散时间高通滤波器

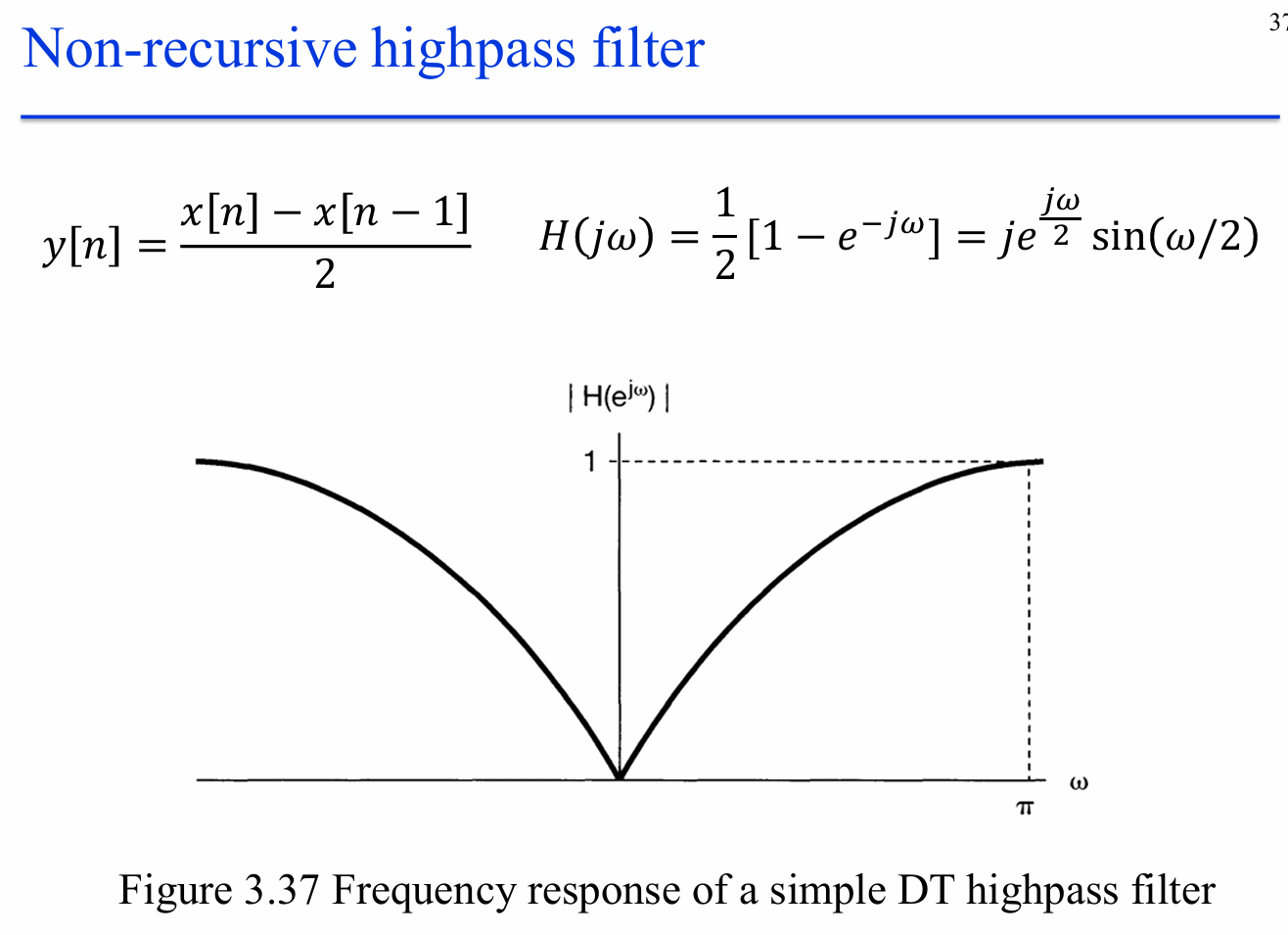
应用

1. 分频让高音喇叭唱高频，低音喇叭唱低频。

仅仅需要一个电路：

2. 按键电话为什么按每个数字都能发出不同的滴声。

每个按键对应低频和高频两个纯音，有四种低频和三种高频，刚好十二种组合。

非周期信号的傅里叶变换

显然这些周期性的 sin cos 函数只能组合成周期性的信号，那么非周期性的呢？

你可能会想，把周期拉的特别长，假装信号是一个大周期不就好了。

听起来十分有道理，那来试着改造一下原来的公式，先把原来傅里叶级数的公式搬过来：

\[x(t)=\sum\limits_{k=-\infty}^{+\infty}a_ke^{jk\omega_0t} \]

\[a_k=\frac 1 T \int_{-T/2}^{T/2} x(t)e^{-jk\omega_0 t}dt \]

但是当 \(T\) 变到无穷大的时候，\(\omega_0\) 会变成 \(0\)，一堆无穷和零堆在一起完全没办法入手。另外，\(k\) 在周期信号里本来表示基频的多少倍，现在基频变成 \(0\) 了，似乎求和式也要变成积分式。这给我们整不会了，没关系，我们不妨先试试最简单的例子，这是连续时间周期方波的式子：

\[x(t) = \begin{cases} 1, & |t| < T_1 \\ 0, & T_1 < |t| < T/2 \end{cases} \]

可以看出 \(T\) 是周期，\([-T_1, T_1]\) 是有值的一段。

它的系数是：

\[a_k = \frac{2\sin(k\omega_0 T_1)}{k\omega_0 T}, \omega_0 = \frac{2\pi}{T} \]

既然 \(\omega_0\) 无穷小，\(k\) 的范围又无穷大，我们不妨设 \(\omega=k\omega_0\)，然后让 \(\omega\) 保持为一个变量。再把剩下一个无穷的 \(T\) 搬到左边：

\[Ta_k = \frac{2\sin(\omega T_1)}{\omega} \]

这下右边全是正常值了！太美丽了！那么我们完全可以把右边的图（自变量 \(\omega\)）画出来，这样 \(Ta_k\) 的值永远分布在这张图上，只不过如果 \(T\) 再大一些，\(\omega_0\) 就会小一些，相同的 \(\omega\) 对应的 \(k\) 就会越大，意味着 \(Ta_k\) 在图上分布得更密集一些。

当 \(T\) 变成无穷时，\(Ta_k\) 在图上就是一个连续函数。

回到原来的一般式，还是让 \(\omega=k\omega_0\)，把基频的多少倍替换为真正的多少频率，就会有：

\[Ta_k=\int_{-T/2}^{T/2} x(t)e^{-j\omega t}dt=\int_{-\infty}^{\infty} x(t)e^{-j\omega t}dt \]

既然 \(Ta_k\) 比 \(a_k\) 更有意义，那我们把 \(Ta_k\) 设为 \(X(j\omega)\)。

这是原本的求和式：

\[x(t)=\sum\limits_{k=-\infty}^{+\infty}a_ke^{jk\omega_0t} \]

我们本来期望它是积分式：

\[x(t)=\int_{-\infty}^{+\infty}a_ke^{jk\omega_0t}dk \]

\(k\) 已经被消掉，现在也不要用 \(k\) 当无穷小量了，用 \(\omega=k\omega_0=k\frac{2\pi}{T}\)。

\[x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}X(j\omega)e^{j\omega t}d\omega \]

这就是合成方程（反傅里叶变换），和上面 \(X(j\omega)\) 的公式放到一起：

\[X(j\omega)=\int_{-\infty}^{\infty} x(t)e^{-j\omega t}dt \]

这就是分析方程（傅里叶变换）。

它们的简洁表示：

\[x(t) \stackrel{\mathcal{F}}{\longleftrightarrow} X(j\omega) \]

\[\mathcal{F}\{x(t)\} = X(j\omega); \quad x(t) = \mathcal{F}^{-1}\{X(j\omega)\} \]

特殊值：

\[X(0) = \int_{-\infty}^{+\infty} x(t) dt; \quad x(0) = \frac{1}{2\pi}\int_{-\infty}^{+\infty} X(j\omega) d\omega \]

离散傅里叶级数 \(a(k)\) 的意义可以想象一堆频率为基频 \(k\) 倍的波拼起来，同样，连续傅里叶级数 \(X(j\omega)\) 的意义就是一堆频率为 \(\omega\) 的波拼起来，只不过不再有基频，也不再有 \(k\)。

地理课雷条件

1. \(x(t)\) 绝对可积

2. \(x(t)\) 在任何有限区间内有有限个极大值和极小值

3. 在任何有限区间内有有限个不连续点。

这样傅里叶变换得到的结果就是收敛的

傅里叶变换的性质

可以自己推的公式

若

\[x(t) \stackrel{\mathcal{FT}}{\longleftrightarrow} X(j\omega) \]

那么

时间反转

\[x(-t) \stackrel{\mathcal{FT}}{\longleftrightarrow} X(-j\omega) \]

Time Shifting

\[x(t-t_0) \stackrel{\mathcal{FT}}{\longleftrightarrow} e^{-j\omega t_0}X(j\omega) \]

由于乘了一个复数，\(X(j\omega)\) 的幅度不变，相位变成 \(\displaystyle \angle X(j\omega)-\omega t_0\)。

Frequency Shifting

\[e^{j\omega_0 t} x(t) \stackrel{\mathcal{FT}}{\longleftrightarrow} X[j(\omega - \omega_0)] \]

Convolution

\[y(t) = h(t) * x(t) \stackrel{\mathcal{FT}}{\longleftrightarrow} Y(j\omega) = H(j\omega) X(j\omega) \]

Duality

\[X(t) \stackrel{\mathcal{FT}}{\longleftrightarrow} 2\pi x(-\omega) \]

\[z(t) = x(t)h(t) \stackrel{\mathcal{FT}}{\longleftrightarrow} Z(j\omega) = \frac{1}{2\pi} [X(j\omega) * H(j\omega)]\]

一些经典变换

\[e^{-at}u(t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{a+j\omega}, \quad a > 0 \]

因此要想求某个傅里叶变换的话，不用急着求积分，可以考虑怎么应用这些性质。