基于等几何的神经介质传输仿真模拟

在复杂几何中的物质运输以保证功能是一个复杂的问题。通过等几何（IGA）模拟物质在生物神经网络中的运输是有意义的。

文章使用反应-扩散-运输(reaction-diffusion-transport)方程表示物质传输过程，用截断分层三次B样条(THB-Spline3D)表示神经的几何形状。并通过Navier-Stokes(NS)方程获得物质传输的速度场，最后使用IGA求解器模拟了单个轴突、二分叉轴突与三分叉轴突的物质传输过程。

1. 总览

文中提出的对神经网络物质传输的建模分析流程图如下所示

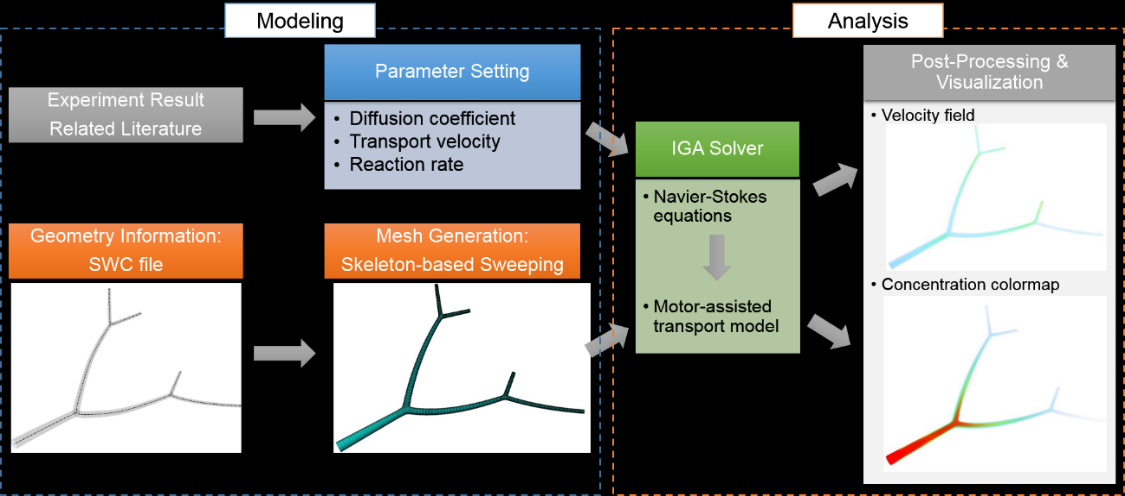
分为两部分：几个建模部分与仿真分析部分

在建模部分，采用基于骨架的扫掠方法来生成轴突的六面体控制网格，然后在控制网格上构建THB-Spline3D用来表示模拟几何体。

在仿真分析部分，通过将一维的辅助动力传输模型推广到三维，得到IGA求解器进行仿真求解。

2. 控制网格生成

为表达轴突中复杂分支的几何形状，使用中心线上的折点以及方向和相关直径等数据可视化模型。如图A所示，将每一段神经网络的中心线当做骨架，通过沿骨架扫掠横截面的四边形网格来生成每个分段的六面体控制网格。

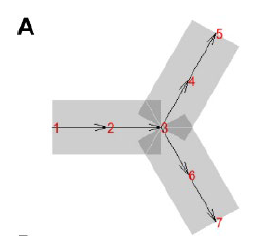
生成网格的目的是指导样条线的生成，以便更准确、更平滑地表示轴突网络几何体。但由于一对一的扫掠要求源曲面与目标曲面具有相同的拓扑，而在轴突的分叉处并不满足这一特性，于是需要在每个分叉处加入一个半平面，如图B、C所示。

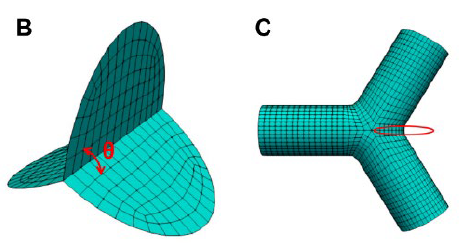
生成的网格要在每个分支点附近达到G1连续性，需要满足一下两点需求：1. 控制网格中两个分支共用的顶点须沿着轴向与相邻的两个折点共线；2. 三个分支共享的边界顶点必须与其所有相邻的边界顶点共面。使用上述的基于骨架的扫掠方式生成的几个简单模型控制网格如下：

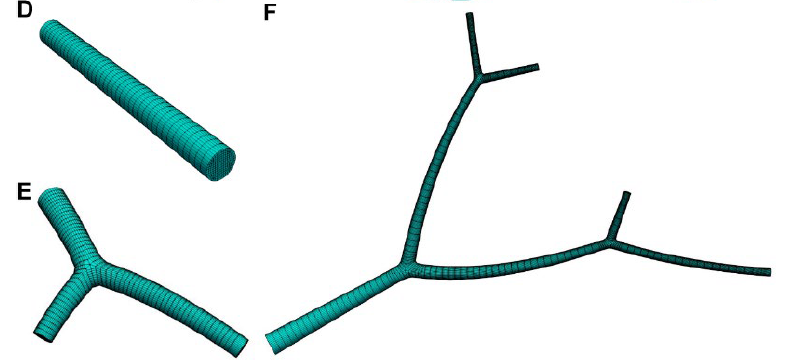
接下来的工作就是使用得到的控制网格构造THB-Spline3D，以最终表示模型。最后使用得到的模型进行物质传输模拟。

2.1 THB-Spline3D综述

截断分层三次B样条(THB-Spline3D)是通过将四边形网格上的双三次混合函数推广到六面体网格上的三次三次混合函数得到的。在三次混合函数的基础上，进一步完成了三次混合函数的层次结构和截断机制，实现了高度局部化的细化。

在六面体网格中，我们定义一条边如果被周围4个六面体共用，则该边为非奇异边，否则为奇异边。而相对应的，若组成六面体的所有边都为非奇异边则该六面体为规则的，否则是不规则的。将六面体网格中的单元（六面体）分为3类：边界单元、内部规则单元、与内部不规则单元。

下图A描述了局部索引为1~8的六面体单元；图B描述了与该六面体单元对应的64个Bézier点，其中红色表示体点，黄色表示面点，绿色表示边缘点，蓝色表示角点。

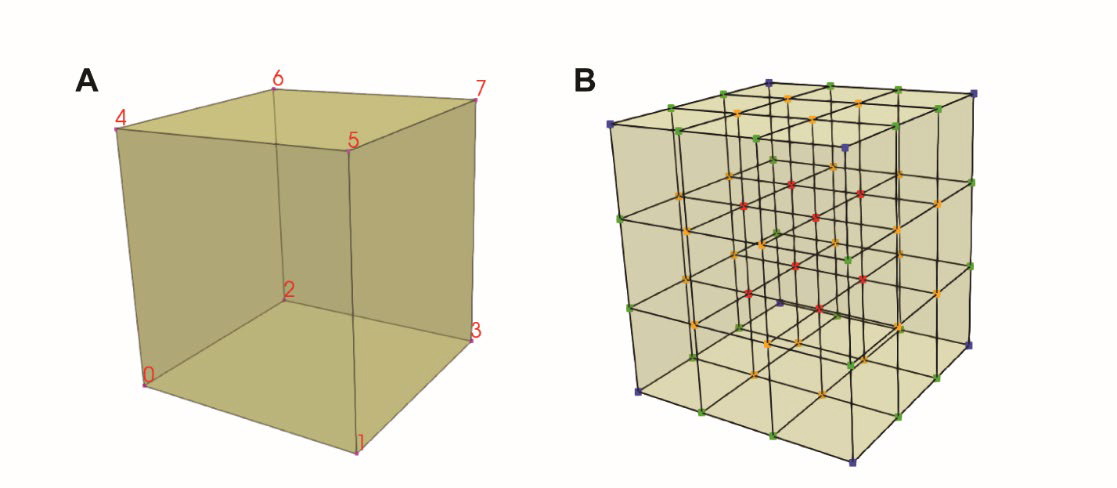
在不规则的单元上应用Bézier提取矩阵\(\mathbf{C}\)可以将局部的样条控制网格转化为Bézier控制网格。对于给定的六面体单元\(\Pi_e\)，64个Bézier点可以通过其局部控制网格中的顶点\(\mathbf{P}\)计算得到：

体点\(\mathbf{R}_{body}^e\)：通过8个顶点\(\mathbf{P}_{body}^e\)的凸组合，\(\mathbf{R}_{body}^e=\mathbf{C}_{body}^e\mathbf{P}_{body}^e\)。\(\mathbf{C}_{body}\)将8个角点转变成8个Bézier体点。

非体点\(\mathbf{R}_{non-body}^e\)：得到所有六面体的Bézier体点后，计算所有体点与非体点之间的欧氏距离。对于每个非体点都可以找到距离最近的体点，得到集合\(\Omega(e,i)\)。之后可以对这些最近的体点求平均得到单个六面体的非体点\(\mathbf{R}_{non-body}^e\)

\[ R_{n o n-b o d y}^{e, i}=\frac{1}{n_{i}} \sum_{(k, j) \in \Omega(e, i)} R_{b o d y}^{k, j} \tag{1} \]

其中\(n_i\)为共享该非体点\(\mathbf{R}_{non-body}^e\)的六面体个数，\((k,j)\)表示六面体\(\Pi_k\)的第\(j\)个非体点。

之后可以通过\(\mathbf{R}^e=\mathbf{CP}\)在局部样条控制网格中导出64个贝塞尔点的凸组合，\(\Pi_e\)上的混合函数定义为\(N^e=\mathbf{C}^Tb\)，其中

\[\begin{aligned} b=&\left[g_{0}(\xi) g_{0}(\eta) g_{0}(\zeta), g_{1}(\xi) g_{0}(\eta) g_{0}(\zeta), \ldots, g_{3}(\xi) g_{0}(\eta) g_{0}(\zeta), g_{0}(\xi) g_{1}(\eta) g_{0}(\zeta), g_{1}(\xi) g_{1}(\eta) g_{0}(\zeta)\right.\\ &\left.\ldots, g_{3}(\xi) g_{3}(\eta) g_{0}(\zeta), g_{0}(\xi) g_{0}(\eta) g_{1}(\zeta), \ldots, g_{1}(\xi) g_{0}(\eta) g_{1}(\zeta), \ldots, g_{3}(\xi) g_{3}(\eta) g_{3}(\zeta)\right]^{T} \end{aligned} \tag{2} \]

\[g_{i}(\omega)=\left(\begin{array}{l} 3 \\ i \end{array}\right)(1-\omega)^{3-i} \omega^{i} \text { for } i=0,1,2,3 \tag{3} \]

在内部规则六面体上的混合函数也可以使用相同的方法导出。对于边界六面体单元用同样的方法计算内部Bézier点，而边界上的Bézier点由四边形表面网格上的双三次调和函数定义。

基于上述给定的六面体网格中的混合函数，我们可以通过下式来构造THB-spline 3D体。

\[V=\sum_{k=1}^{n_p-1} P_k N_k \tag{4} \]

3. IGA求解器

3.1 在三维几何中的动力辅助物质运输(Motor-Assisted Material Transport)

传统的动力辅助运输是一维中描述囊泡和细胞器之间宏观传输的，而Motor指代排列的细胞内细丝，特别是微管或肌动蛋白细丝组成的网络上的分子马达。

动力辅助运输模型可以由一组“反应——扩散——传输”方程描述，这些方程使用简单的动力学描述物质颗粒与细胞细丝的相互作用，并允许未附着的颗粒的自由扩散和附着颗粒的定向运动。

下图是整个动力辅助运输模型的描述，运输的正方向为自左向右

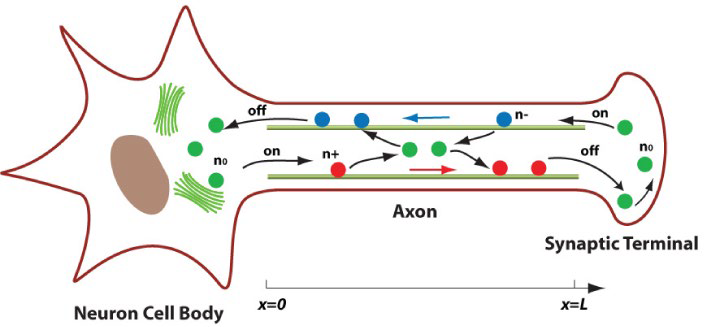
其中绿色圆点表示浓度为\(n_0\)处于自由扩散状态的物质颗粒，红色圆点表示浓度为\(n_+\)在微管上处于顺行状态的物质颗粒，蓝色圆点表示浓度为\(n_-\)在微管上处于逆行状态的物质颗粒。

将该运输模型推广到三维，可以得到

\[\left\{\begin{array}{ll} \frac{\partial n_{0}}{\partial t}-D \nabla^{2} n_{0}=-\left(k_{+}+k_{-}\right) n_{0}+k_{+}^{\prime} n_{+}+k_{-}^{\prime} n_{-} & \text {in } \Omega \\ \frac{\partial n_{+}}{\partial t}+v_{+} \cdot \nabla n_{-}=k_{+} n_{0}-k_{+}^{\prime} n_{+} & \text {in } \Omega \\ \frac{\partial n_{-}}{\partial t}+v_{-} \cdot \nabla n_{-}=k_{-} n_{0}-k_{-}^{\prime} n_{-} & \text {in } \Omega \end{array}\right. \tag{5} \]

其中，\(\Omega \subset R^3\)是神经元细胞中的内点；\(n_0,n_+,n_-\)分别是空间中自由扩散的粒子、正向运输粒子、反向运输粒子的空间浓度；\(D\)是自由扩散因子；\(v_+,v_-\)分别是正向运输粒子和反向运输粒子的速度；\(k_{\pm},k_{\pm}^{\prime}\)分别表示运输粒子正反方向的附着率与剥离率。

为了模拟物质在单个神经元中的运输过程，需要确定合适的边界条件解方程(5)。假设正反两个方向的物质运输具有稳定的空间浓度，有

\[\left\{\begin{array}{ll} n_{0}=n, & n_{+}=\lambda n \text { at incoming end } \\ n_{0}=\tilde{n}, & n_{-}=\tilde{\lambda} \tilde{n} \text { at outgoing end } \end{array}\right. \tag{6} \]

\(\lambda,\tilde{\lambda}\)是细胞中细丝对向两端运动物质的附着程度（负载程度）。将神经元中的物种看做是不可压缩的流体，假设物质的运输速度是匀速，扩散系数为常数，然后求解稳态Navier-Stokes方程，得到单个轴突内部物理上真实的速度场。

\[\left\{\begin{array}{ll} \nabla \cdot u=0 & \text { in } \Omega \\ \nabla \cdot(u \otimes u)+\nabla p=v \Delta u+f & \text { in } \Omega \end{array}\right. \tag{7} \]

\(\Omega \subset R^3\)是不可压缩流体域，\(u\)是流体速度，\(p\)是压力，\(f\)是单位体积的外力（body force，如重力等），\(v\)是运动黏度，\(\otimes\)是张量积。

在边界条件方面，对圆形截面上的每个点施加一个抛物线形式的初速度\(v(r)=v_{t}\left(1-(r / R)^{2}\right)\)速度方向与横截面垂直，其中\(v_t\)是进口处的输送速度，\(R\)是圆横截面半径，\(r\)是圆横截面中心到该点的距离。

上式（7）中的速度\(u\)将会表示式（5）中的速度，\(v_+=u,v_-=-u\)。

3.2 稳定公式

在空间离散上使用IGA，时间离散上使用全隐式方法。但在解方程（5）的时候仍存在问题。方程（5）和（7）中的对流项使刚度矩阵不对称，而导致解的震荡（不确定性）。为解决该问题使用基于变分多尺度（variational multiscale , VMS）残差方法。

令\(V\)同时表示试解空间又表示权函数空间。VMS方法将\(V\)分解为“粗尺度”子空间\(\overline{V}\)和“细尺度”子空间\(V^\prime\)，即\(V=\overline{V}+V^\prime\)。假设\(\overline{V}\)是由基函数定义的有限维空间，\(V^\prime\)是未知表达式构成的无限维空间，则细尺度空间\(V^\prime\)可以表示为\(\overline{V}\)与残差\(\mathbf{Res}(\overline{V})\)的函数\(V^\prime=F^\prime(\overline{V},\mathbf{Res}(\overline{V}))\)

将式（5）中的速度和压力分为两部分\(u=\overline{u}+u^\prime\)，\(p=\overline{p}+p^\prime\)。同时分别在式（5）中乘上两个权函数\(\overline{\omega}，\overline{\psi}\)，然后在域上积分并将这些项组合起来，我们就可以得到一个弱形式

\[B\left(\{\bar{\omega}, \bar{\psi}\},\left\{\bar{u}+u^{\prime}, \bar{p}+p^{\prime}\right\}\right)-L(\bar{\omega})=0 \tag{8} \]

和

\[\begin{aligned} B\left(\{\bar{\omega}, \bar{\psi}\},\left\{\bar{u}+u^{\prime}, \bar{p}+p^{\prime}\right\}\right) &=(\bar{\omega}, \bar{u} \cdot \nabla \bar{u})_{\Omega}-(\nabla \cdot \bar{\omega}, \bar{p})_{\Omega}+\left(\nabla^{s y m} \bar{\omega}, 2 \nu \nabla^{s y m} \bar{u}\right)_{\Omega} \\ &+(\bar{\psi}, \nabla \cdot \bar{u})_{\Omega}+\left(\bar{\omega}, u^{\prime} \cdot \nabla \bar{u}\right)_{\Omega}-\left(\nabla \bar{\omega},\left(\bar{u}+u^{\prime}\right) \otimes u^{\prime}\right)_{\Omega} \\ &-\left(\nabla \cdot \bar{\omega}, p^{\prime}\right)_{\Omega}-(\nabla \bar{\psi}, \nabla \cdot \bar{u})_{\Omega} \end{aligned} \tag{9} \]

\[L(\bar{\omega})=(\bar{\omega},f)_\Omega \tag{10} \]

其中\(\nabla^{s y m}(\cdot)\)是由\(\nabla^{s y m} \bar{u}=\left(\nabla \bar{u}+(\nabla \bar{u})^{T}\right) / 2\)给出的对称梯度算子。

为了处理式（5）中的对流项，使用稳定公式解决数值震荡与不稳定性的问题。

在计算稳定性参数\(\tau\)上，首先令\(\omega^h\)为权函数，\(n_0^h,n_\pm^h\)分别是\(n_0,n_\pm\)的试解，则式（5）的稳定公式可以写成

\[\int_{\Omega} \omega^{h} \frac{\partial n_{0}^{h}}{\partial t} d \Omega+\int_{\Omega} \nabla \omega^{h} \cdot D \nabla n_{0}^{h} d \Omega+\int_{\Omega} \omega^{h}\left(k_{+}+k_{-}\right) n_{0}^{h} d \Omega-\int_{\Omega} \omega^{h}\left(k_{+}^{\prime} n_{+}^{h}+k_{-}^{\prime} n_{-}^{h}\right) d \Omega=0 \tag{11} \]

\[\int_{\Omega} \omega^{h}\left(\frac{\partial n_{+}^{h}}{\partial t}+v_{+}^{h} \cdot \nabla n_{+}^{h}-k_{+} n_{0}^{h}+k_{+}^{\prime} n_{+}^{h}\right) d \Omega+\sum_{i=1}^{n_{e l e}} \int_{\Omega_{i}} \tau_{S U P G} v_{+}^{h} \cdot \nabla \omega^{h}\left(\frac{\partial n_{+}^{h}}{\partial t}+v_{+} \cdot \nabla n_{+}^{h}-k_{+} n_{0}^{h}+k_{+}^{\prime} n_{+}^{h}\right) d \Omega=0 \tag{12} \]

\[\int_{\Omega} \omega^{h}\left(\frac{\partial n_{-}^{h}}{\partial t}+v_{-}^{h} \cdot \nabla n_{-}^{h}-k_{-} n_{0}^{h}+k_{-}^{\prime} n_{-}^{h}\right) d \Omega+\sum_{i=1}^{n_{e l e}} \int_{\Omega_{i}} \tau_{S U P G} v_{-}^{h} \cdot \nabla \omega^{h}\left(\frac{\partial n_{-}^{h}}{\partial t}+v_{-} \cdot \nabla n_{-}^{h}-k_{-} n_{0}^{h}+k_{-}^{\prime} n_{-}^{h}\right) d \Omega=0 \tag{13} \]

\(n_{ele}\)是网格单元数，\(\Omega_i\)是第\(i\)个单元的域，\(\tau_{SUPG}\)是streamline upwind/Petrov-Galerkin (SUPG)方法中的稳定参数。定义长度尺度

\[h=2\left\|v_{\pm}^{h}\right\|\left(\sum_{k=1}^{n_{e n}}\left|v_{\pm}^{h} \cdot \nabla N_{k}\right|\right)^{-1} \tag{14} \]

\(N_k\)是结点\(k\)对应的基函数，\(n_{en}\)是当前网格单元中的节点数。则稳定参数为：

\[\tau_1=\frac{h}{2\left\|v_{\pm}^{h}\right\|} \qquad \tau_2=\frac {\Delta t}{2} \qquad \tau_{SUPG}=\left( \frac{1}{\tau_1^2}+\frac{1}{\tau_2^2} \right)^{-1/2} \tag{15} \]

\(\Delta t\)是时间步长。

有了上述的理论基础就可以求解运输模拟。