bzoj 2566 calc 拉格朗日插值

calc

Time Limit: 30 Sec  Memory Limit: 512 MB
Submit: 377  Solved: 226
[Submit][Status][Discuss]

Description

　　一个序列a1,...,an是合法的，当且仅当：
　　长度为给定的n。
　　a1,...,an都是[1,A]中的整数。
　　a1,...,an互不相等。
　　一个序列的值定义为它里面所有数的乘积，即a1a2...an。
　　求所有不同合法序列的值的和。
　　两个序列不同当且仅当他们任意一位不一样。
　　输出答案对一个数mod取余的结果。

 

Input

 

　　一行3个数，A，n，mod。意义为上面所说的。

 

Output

　　一行结果。

 

Sample Input

9 7 10007

Sample Output

3611

HINT

 

数据规模和约定

　　0:A<=10,n<=10。

　　1..3:A<=1000,n<=20.

　　4..9:A<=10^9,n<=20

　　10..19:A<=10^9,n<=500。

　　全部:mod<=10^9,并且mod为素数，mod>A>n+1

 

Source

 

不得不说dp设的也是十分好的，估计自己还想不出。

f[i][j]表示，前i个元素中，选择了j个的方案数，这个转移是怎么样的呢？

f[i][j]=f[i-1][j-1]*i*j+f[i-1][j]，这个转移中的第二个十分显然，第一个是什么意思，就是选择了i这个元素，

插入到j中的任意一个位置，就是j个位置离随便哪个位置都可以，然后根据乘法的分配律，结合一下，就可以了。

当然j可以大于i，就因为i可以插到后面的位置。

 

就算想出了这一步，下面发现这个表是一个几次的多项式我基本上不可能会发现

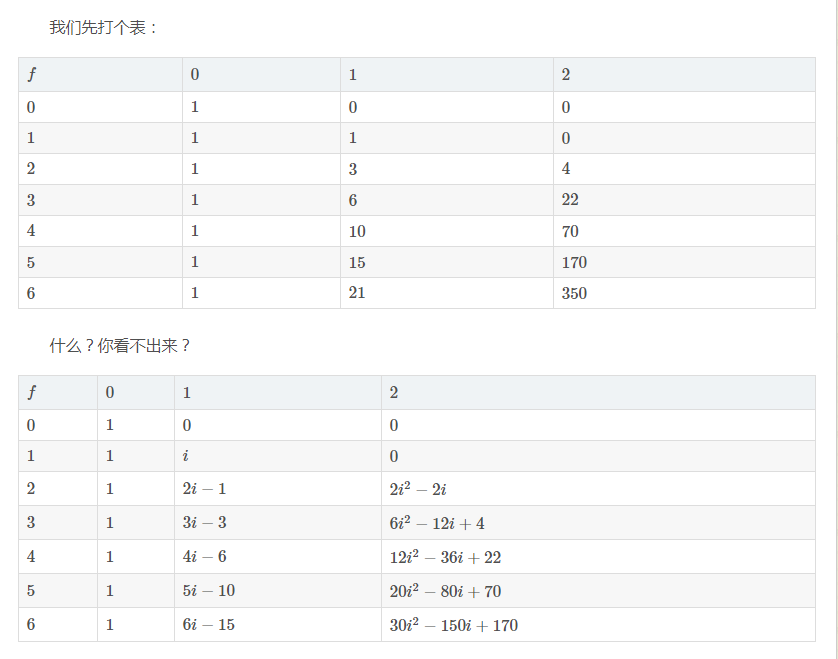
某大佬打了这个表，然后这个多项式怎么搞出来的真的有点厉害

但是这个多项式是没用的，因为这个多项式的系数是变化的，所以没有什么用

有没有一个多项式的系数是不变的呢？
然后就有大佬发现了

 

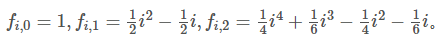
发现了这个，即f[i][j]的系数只和j有关，是一个最高项系数是2*j的多项式，然后就稳了，

这样只需要求出2*n+1个点就可以插值了，朗格朗日插值求一下m这个位置的值即可。

 

 

#include<cstring>
#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>

#define N 1007
#define ll long long
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
    return x*f;
}

int n,m;
ll p,ans;
ll f[N][N];

ll fast_pow(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if (b&1) (ans*=a)%=p;
        (a*=a)%=p;
        b>>=1;
    }
    return ans;
}
void Lagrange()
{
    for (int i=0;i<=2*n;i++)
    {
        ll s1=1,s2=1;
        for (int j=0;j<=2*n;j++)
            if (j!=i)
            {
                (s1*=(m-j))%=p;
                (s2*=(i-j))%=p;
            }
        (ans+=f[i][n]*s1%p*fast_pow(s2,p-2)%p)%=p;    
    }
}
int main()
{
    m=read(),n=read(),p=read();
    f[0][0]=1;
    for (int i=1;i<=2*n;i++)
    {
        f[i][0]=f[i-1][0];
        for (int j=1;j<=n;j++)
            f[i][j]=(f[i-1][j-1]*i%p*j+f[i-1][j])%p;
    }
    if (m<=2*n)
    {
        printf("%lld\n",f[m][n]);
        return 0;
    }
    
    Lagrange();
    ans=(ans%p+p)%p;
    
    printf("%lld\n",ans);
}