bzoj 4407 于神之怒加强版 （反演+线性筛）

于神之怒加强版

Time Limit: 80 Sec  Memory Limit: 512 MB
Submit: 1184  Solved: 535
[Submit][Status][Discuss]

Description

给下N,M,K.求
 
 

 

Input

输入有多组数据，输入数据的第一行两个正整数T,K，代表有T组数据，K的意义如上所示，下面第二行到第T+1行，每行为两个正整数N,M，其意义如上式所示。

 

Output

如题

 

Sample Input

1 2
3 3

Sample Output

20

HINT

 

1<=N,M,K<=5000000,1<=T<=2000


题解：JudgeOnline/upload/201603/4407.rar


 

 

Source

命题人：成都七中张耀楠，鸣谢excited上传。

 
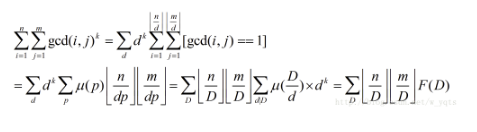
 1 #include<bits/stdc++.h>
 2 #pragma GCC optimize(2)
 3 #pragma G++ optimize(2)
 4 #include<iostream>
 5 #include<algorithm>
 6 #include<cmath>
 7 #include<cstdio>
 8 #include<cstring>
 9 
10 #define ll long long
11 #define inf 1000000000
12 #define mod 1000000007
13 #define N 5000007
14 using namespace std;
15 inline int read()
16 {
17     int x=0,f=1;char ch=getchar();
18     while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
19     while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
20     return x*f;
21 }
22 
23 int F[N],f[N],flag[N],k,tot,p[N],ans;
24 inline int gpow(int x,int y)
25 {
26     int ans=1;
27     while (y)
28     {
29         if (y&1) ans=(ll)ans*x%mod;
30         y>>=1;x=(ll)x*x%mod;
31     }
32     return ans;
33 }
34 void preparation()
35 {
36     F[1]=1;
37     for (int i=2;i<N;i++)
38     {
39         if (!flag[i]){f[i]=gpow(i,k);F[i]=f[i]-1;p[++tot]=i;}
40         for (int j=1;j<=tot&&i*p[j]<N;j++)
41         {
42             flag[i*p[j]]=1;
43             if (i%p[j])F[i*p[j]]=(ll)F[i]*F[p[j]]%mod;
44             else{F[i*p[j]]=(ll)F[i]*f[p[j]]%mod;break;}
45         }
46     }
47     for (int i=1;i<N;i++) (F[i]+=F[i-1])%=mod;
48 }
49 int main()
50 {
51     int Case=read();k=read();
52     preparation();
53     while (Case--)
54     {
55         int n=read(),m=read();if (n>m) swap(n,m);ans=0;
56         for (int i=1,pos=0;i<=n;i=pos+1)
57         {
58             pos=min(n/(n/i),m/(m/i));
59             (ans+=1LL*(n/i)*(m/i)%mod*(F[pos]-F[i-1])%mod)%=mod;
60         }
61         printf("%d\n",(ans+mod)%mod);
62     }
63     return 0;
64 }

 

posted @ 2018-03-08 21:22  Kaiser-  阅读(144)  评论(0)  编辑  收藏  举报