源哥每日一题第十七弹 poj 1568 Alpha-Beta剪枝

链接：http://poj.org/problem?id=1568

题目：为什么是英文啊题目就是给你一个4*4的OX棋盘，上面已经下了一些棋，然后现在轮到X下，问你有没有一个必胜的方法，有的话就输出坐标，没有输出#####

北大的又一神题。一个很简单的思路很容易就能想到，遍历所有可能的下法，暴力搜看有没有一种情况，无论O怎么下，X都能赢。但是这样复杂度太高了。

然后一个非常神奇的关于棋盘类的博弈搜索方法就出来了：

先说说极大极小搜索法：和正常搜索不同的是，这种搜索限制了搜索深度。当然，搜索到了限定深度之后，非常有可能找不到结果。怎么办呢？给出一个当前状态的得分（估价函数）作为评价当前状态优劣的指标。放到本题，就是对于X越有利的状态，得分越高；对X越不利的状态，得分越低。一个比较成熟的思路就出现了：到X下的时候，找所有儿子里得分最高的；到O下的时候，找所有儿子里得分最低的。

差不多就是这个样子（图片来自北大课件）：

 Alpha–beta给出了准确的剪枝方法。

这个剪枝分为两部分：

alpha剪枝：如图：当搜到X的时候，由于R=K>X,所以R的值不会因为X子节点值的改变而改变，所以，可以剪掉X除Y之外的枝。即：当前为极小值X节点，其兄弟节点中，已经找到了最大值a那么在搜索X的时候，如果某个子节点Y<=a,则不用考虑后面的节点了。（极大值剪枝）

 

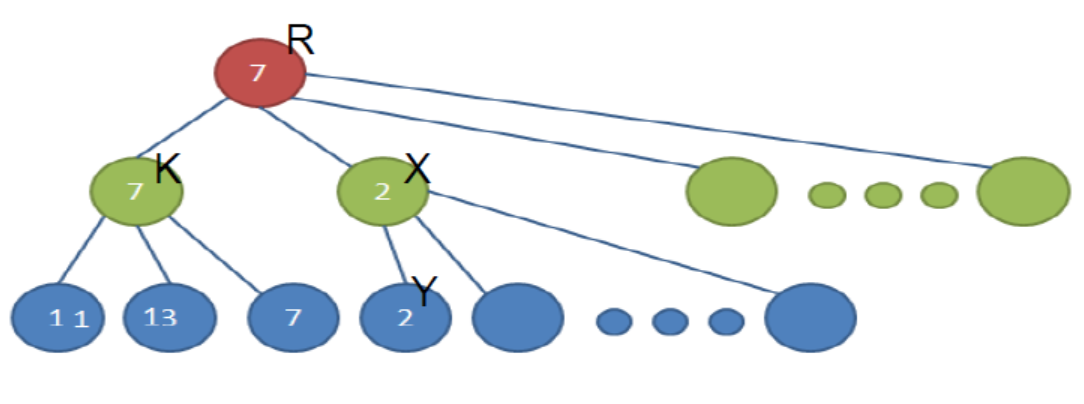
beta剪枝：当前为极大值X节点，其兄弟节点中，已经找到了最小值b那么在搜索X的时候，如果某个子节点Y>=b,则不用考虑后面的节点了。（极小值剪枝）

回到这个题。这个题估价函数只有三种情况，既1（胜），0（平），-1（负）也就是说，只要找到一个估价为1的方法就可以。

p.s. 出现了一个神级优化：chess<=4

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
string mp[5];
int X,Y,chess;
int Mindfs(int x,int y, int alpha);
int Maxdfs(int x,int y, int beta);
int jud(char a) {
    if(a=='o') return 1;
    else if(a=='x') return -1;
    else return 0;
}
int chk(int x,int y) {
    int ans = 0;
    for (int i = 0; i < 4; i++) 
        ans+=jud(mp[x][i]);
    if(abs(ans)==4) return 1;
    ans = 0;
    for (int i = 0; i < 4; i++)
        ans+=jud(mp[i][y]);
    if(abs(ans)==4) return 1;
    ans = 0;
    for (int i = 0; i < 4; i++)
        ans+=jud(mp[i][i]);
    if(abs(ans)==4) return 1;
    ans = 0;
    for (int i = 0; i < 4; i++)
        ans+=jud(mp[i][3-i]);
    if(abs(ans)==4) return 1;
    return 0;
}

int Mindfs(int x,int y,int alpha) {
    int ans = 1;
    if (chk(x,y)) return 1;
    if (chess == 16) return 0;
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            if(mp[i][j] == '.') {
                mp[i][j] = 'o'; 
                chess++;
                int t = Maxdfs(i,j,ans);
                mp[i][j] = '.';
                chess--;
                ans = min(ans,t);
                if(ans <= alpha) {
                    return ans;
                }
            }
        }
    }
    return ans;
}

int Maxdfs(int x,int y,int beta) {
    int ans = -1;
    if (chk(x,y)) return -1;
    if (chess == 16) return 0;
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            if(mp[i][j] == '.') {
                mp[i][j] = 'x';
                chess++;
                int t = Mindfs(i,j,ans);
                mp[i][j] = '.';
                chess--;
                ans = max(ans,t);
                if(ans >= beta) {
                    return ans;
                }
            }
        }
    }
    return ans;
}

int sol() {
    int alpha = -1;
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            if(mp[i][j] == '.') {
                mp[i][j] = 'x';
                chess++;
                int t = Mindfs(i,j,alpha);
                mp[i][j] = '.';
                chess--;
                if(t == 1) {
                    X = i; 
                    Y = j;
                    return 1;
                }
            }
        }
    }
    return 0;
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("D:\\fengyu\\Jiang_C\\.vscode\\in.txt","r",stdin);
	freopen("D:\\fengyu\\Jiang_C\\.vscode\\out.txt","w",stdout);
#endif
    string s;
    while(cin >> s && s[0] != '$') {
        chess = 0;
        for (int i = 0; i < 4; i++) {
            cin >> mp[i];
            for (int j = 0; j < 4; j++) {
                chess += mp[i][j] != '.';
            }
        }
        if(chess <= 4 || !sol()) {
            puts("#####");
        } else {
            printf("(%d,%d)\n",X,Y);
        }
    }
    return 0;
}