递归
函数调用原理
在理解递归之前,不得不先了解一下函数调用的工作原理。
在程序运行期间调用一个函数的时候,在运行被调用函数之前,需要完成三项任务。
1.将所有的实参、返回地址等信息传递给被调用函数。
2.为被调用函数的局部变量分配存储区。
3.将控制转移到被调用函数的入口。
函数执行完返回之前,应该完成下列三项任务。
1.保存当前函数的最终计算结果。
2.释放被调函数的数据区。
3.根据返回地址将控制转移到上层,也就是调用方。
在函数之中调用函数也是同样的道理,如A函数中调用B函数,B函数中调用C函数。
那么C函数执行完之后程序的控制会回到B函数中调用C的地方继续往下执行,B执行完后会回到A中继续执行,整个流程的运行规则是后调用先返回。
能够实现后进先出的数据结构是栈,此时的内存管理实行的就是 “栈式管理” ,这是栈的一个典型应用。
递归函数
一个直接调用自己或间接调用自己的函数,称为递归函数。
递归必须要满足两个元素,一是递归出口,二是递归表达式。
递归出口即为返回条件,没有递归出口的递归那是死循环。 递归表达式即是直接或者间接调用自身的行为,如果你不调用自身,那么这个算法也不能够叫做递归。
所谓间接调用自己,意思就是你调用别的函数,别的函数里面又在调用你。
我们设计递归函数可以根据几种情况考虑:
第一种情况,问题的定义是递归的,比如数学中的阶乘,像这样子的问题我们直接就可以写出递归函数。
第二种情况,有些数据结构比如二叉树广义表,由于结构本身存在递归特性,则可以使用用递归函数来描述。
第三种情况,问题本身没有明显的递归特征,但使用递归求解更简单,比如Hanoi塔问题。
前两种情况比较直观,只要我们一遇到,就会很直接的想到用递归来处理,第三种情况则需要更多的经验来判断是否应该使用递归。
阶乘函数
一个正整数的阶乘是所有小于或等于该数的正整数的乘积,0的阶乘为1。
比如5的阶乘 = 5 * 4 * 3 * 2 * 1 = 120;
递归代码:
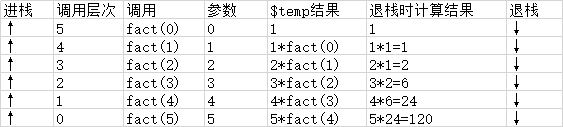
function fact($n){ if(0 == $n){ return 1;//递归出口 } $temp = $n * fact($n-1);//递归表达式 return $temp; } $result = fact(5);
如果描绘出递归工作栈的变化情况会非常的直观:
Hanoi塔问题
Hanoi塔 也叫做汉诺塔。
题目:
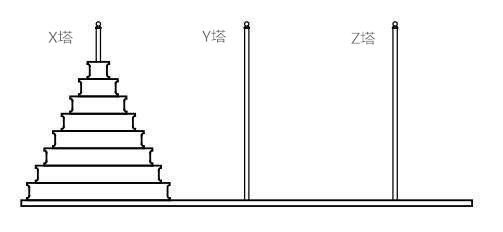
如图所示,假设有三个分别命名为X、Y和Z的塔座,在X上插的有N个直径大小各不相同,并从大到小依次堆叠的圆盘,现要求将X塔上的所有盘子移动到Z塔上,并且堆叠的顺序保持不变。
圆盘移动时必须遵循以下规则:
1、每次只能移动一个圆盘
2、圆盘可以放到X,Y,Z中任一塔座上
3、任何时候不能将一个较大的圆盘压在较小的圆盘之上
在我们不知道递归之前,按照常规做法,我们都会使用递推的方式,比如1个圆盘的情况怎么解决,2个圆盘的情况怎么解决,3个圆盘的情况怎么解决,将多种情况递推出来,然后找规律。
我们将盘子的个数称为N,盘子大小即为n的大小。
当N=1时,直接将1号盘子搬到Z号塔就结束了。
当N=2时,将1号盘子搬到Y上,再将2号盘子搬到Z上,再将1号盘子从Y搬到Z上。
当N=3时,将1号盘子搬到Z上,2号盘子搬到Y上 ,1号盘子从Z搬到Y上,3号盘子搬到Z上,1号盘子搬到X上,2号盘子从Y搬到Z上,1号盘子从X搬到Z上。
.........
我们发现,根据N的不同,盘子的搬法是不一样的,使用递推的方法,很难找到规律。
据说国外有个皇帝曾经为了解这个题,叫手下的人实际操作搬盘子,然而搬了N多天也没个结果。 因为他们的盘子有点多,用了64个盘子。
后来得出的结论是,移动盘子的次数是2的N次方-1,就算1秒钟移动一次,要搬完这64个盘子,需要5845.54亿年,那时候地球早已经毁灭了。
既然常规思路走不通,我们就换个思路考虑问题。
我们可以把问题分解成下面三步
第一步,我们想办法把N-1个盘子从X搬到Y上。
第二步,把X上的最后一个盘子搬到Z上。
第三步,把Y上的N-1个盘子搬到Z上。
这三步实现的话,那么整个事情也就完成了。
不管你的N有多大,我们只把它拆分为N-1和1两个规模,当剩下的盘子等于1时,那么我们就直接搬到Z上就行了。
那么我们面临的最大的问题,就是第一步和第三步中的搬动N-1个盘子,要怎么搬?
此时此刻,我们面临的这个问题,和最开始的问题完全一样。但问题规模不一样了,原来是N个盘子的问题,现在我们把它变成了N-1个盘子的问题。
同样,N-1的问题,不就等于N-2的问题吗?不就等于N-3的问题吗?
那么我们进一步分析
第一步中,把N-1个盘子从X搬到Y上,此时起始位置是X,目标位置是Y,中间要借助Z。
第二步就简单了,直接把X上的盘子移动到Z上。
第三步中,再把Y上的N-1个盘子搬到Z上,此时起始位置是Y,目标位置是Z,中间要借助X。
他们的每一次移动,都要遵守这三步的规则,做法都是一样,唯有传递的不同。
有了上面这些思考,我们再来看代码,配合着注释,我想更容易帮助理解。
/** * @param $n 盘子编号 * @param $x 起始位置 * @param $y 辅助塔 * @param $z 目标位置 */ function hanoi($n,$x,$y,$z){ if($n==1){ move($x,1,$z); //将最后一个圆盘从x搬到z上 }else{ hanoi($n-1,$x,$z,$y);//将x上N-1个盘子从x搬到y上 z是辅助塔 move($x,$n,$z);//将编号为N的盘子从x搬到z上 hanoi($n-1,$y,$x,$z);//将y上N-1个盘子从y搬到z上 x是辅助塔 } } function move($x,$n,$z){ echo '移动第'.$n.'号盘子 从'.$x.'-->'.$z.'<br>'; } hanoi(5,'x','y','z');
友情提示:不要去想具体的移动,你一但去想,就陷入了递推的思维中,那样你会疯掉的。对于递归的理解最重要的是放弃你在脑海中推导细节的冲动,汉诺塔问题永远只有两层,就是N-1和1,当N>1时他们以同样的方式移动。
递归思维
在讨论Hanoi塔问题的时候我们面临了两种思维的选择,递推与递归,这里进行比较一下,这两种思维到底有什么区别。
以登山为例,如华山9000级台阶,如何登上这9000级台阶?
递推思维:我先抬脚登上1级台阶,就还剩8999级台阶,然后再登1级台阶,就还剩8998级台阶,登一级台阶又不费力,只需重复这个动作,最终即可登顶。
递归思维:如果我现在在第8999级台阶上,我只需要抬脚一步就可以登顶。那么我怎样才能到第8999级台阶上呢? 如果我现在在第8998级台阶上,我只需要抬脚一步就可以到达8999级台阶,以此类推。
虽然说,最终实践起来都是一步一步往上爬,没什么区别,但两种思维讨论问题的出发点不一样,递推从易到难,递归从难到易,编写出来的算法程序是两个派别。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号