南京大学 AI 导论 Cart-Pole V1 游戏（强化学习）

19:35 2025.01.25

目的：阐述 DQN 算法原理

Q-learning 算法

bellman 方程

我们想解决一个马尔可夫过程的最优决策问题。

在这个问题中，状态序列是可以无限长的，因此我们定义一个状态序列的价值 \(V\) 为：

\[V([s_0, a_0, s_1, ...])=\sum_{i\ge 0} \gamma^i R(s_i, a_i, s_{i+1}) \]

这里的 \(R(s_i,a_i,s_{i+1})\) 表示 \(s_i\xrightarrow{a_i} s_{i+1}\) 情况的此步奖励大小。

在这里引入 \(\gamma(\in (0, 1))\) 是为了让越远的未来贡献越低，并且是一定可以收敛的。

此时定义一个动态规划函数 \(Q(s,a)\) 表示在目前处于状态 \(s\) 且选择动作 \(a\) 的期望价值最高是多少，则可以有等式：

\[Q(s,a)=\sum_{s'}P(s'|s,a)(R(s,a,s')+\gamma\max_{a'}Q(s',a')) \]

即枚举每个可能的后继状态 \(s'\)，对应的最大奖励期望 \(E[R|s\xrightarrow{a}s']\) 即为此步奖励 \(R(s,a,s')\) 加上折扣系数 \(\gamma\) 乘以下一步的最优决策 \(\max_{a'}Q(s',a')\)。

学习策略

我们已经拥有了 bellman 方程，且可以证明该方程具有唯一解（若有两个解，可以找到对应的 \(Q(s_0,a_0)\) 不一样，并比较它们的状态序列，价值更低的那个就是错的）。

但是，由于多种原因，例如状态数过多，状态转移不形成 DAG 等多种原因，我们难以使用朴素的动态规划。因此我们采用迭代的方式解出这个方程。

初始令 \(Q(*，*)=0\)，然后每次做这个过程 \(Q'(s,a)\leftarrow\sum_{s'}P(s'|s,a)(R(s,a,s')+\gamma\max_{a'}Q(s',a'))\)，有数学证明说明这种迭代的收敛效率并不低。

此外，可以引进学习速率参数 \(\alpha\)，此时学习过程为：

\[Q'(s,a)\leftarrow(1-\alpha)Q(s,a)+\alpha\sum_{s'}P(s'|s,a)(R(s,a,s')+\gamma\max_{a'}Q(s',a')) \]

DQN(Deep Q Network) 算法

上面的方法在状态离散时好用，但是当状态连续的时候，就无法存储每个 \(Q\) 值了。

我们使用深度神经网络解决这个问题。我们希望向神经网络输入 \(s,a\) 后，可以得到一个 \(Q^*(s,a)\)，并且 \(|Q(s,a)-Q^*(s,a)|\) 偏差很小，这里 \(Q\) 代表 bellman 方程的真实解。

那么每次执行一个动作时，过程是 \(s\xrightarrow{a}s'\)，奖励是 \(r\)，因此就使用 \((y-Q(s,a))^2\) 作为损失函数更新神经网络。其中：

\[y=r+\gamma\max_{a'}Q(s',a') \]

那么我们怎么获取这些训练数据呢？考虑直接玩这些游戏，每次有 \(\epsilon\) 的概率随机选择一个随机操作，进行探索；有 \(1-\epsilon\) 的概率选择 \(\arg\max_a Q(s,a)\) 执行当前最优操作。

但是不能每一步 \((s,a,s',r)\) 都进行训练，因为训练数据应当是独立同分布的，因此维护一个经验池，大小为 buffer_size，每次训练从经验池中随机选择一个进行训练。

最后，DQN 算法还维护了两个神经网络，分别存储当前 Q 值和目标 Q 值。

在线 Q 网络 (Online Q-Network):作用： 用于选择动作（通过 \(\epsilon\)-贪心策略）并计算当前的 预测 Q 值 \(Q(s, a; \theta)\)。

更新： 实时通过梯度下降进行更新。

目标 Q 网络 (Target Q-Network):作用： 用于计算目标 Q 值 \(y_i\)，这是贝尔曼方程中的参照项。

更新： 延迟更新。它的参数 \(\theta^-\) 每隔 \(C\) 步才从在线网络 \(\theta\) 复制一次。

原因是，当我们更新 \(\theta\) 来让 \(Q(s, a)\) 接近目标值 \(y_i\) 时，目标值 \(y_i\) 本身也同时改变了。这导致 Q 值函数在状态空间中不稳定地振荡或发散，难以收敛。使用目标网络 \(\theta^-\) 延迟更新，暂时固定了目标值 \(y_i\) 的计算，使其在一段时间内保持稳定。这提供了一个稳定的学习目标，极大地提高了算法的稳定性和收敛性。

20:45 2025.12.05

目的：回答以下问题：
main.py 代码中 lr, gamma, buffer_size 三个变量分别有何作用？
agent.py ，act 和 act_no_explore 两个函数有何不同？训练过程中采用act_no_explore函数会有什么问题？

gamma 就是上述的折扣系数，越大代表越重视未来的收益，但收敛也越慢。

buffer_size 是经验池的大小，因为太久之前的经验是根据很久以前的 Q 值决策的，而那个 Q 值不那么准确，决策也没那么明智，比如考虑最开始 Q 是完全随机时候的决策，因此就需要固定经验池大小。

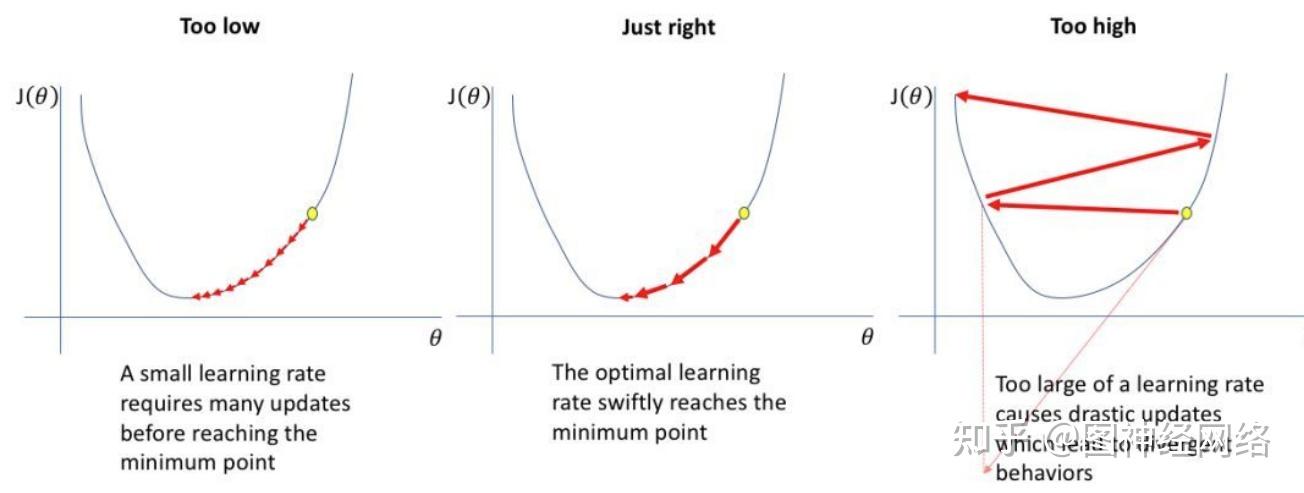
lr 是学习率，决定深度神经网络的学习速率。

act 是采用了 \(\epsilon\)-贪心 策略，有一定概率探索一个随机的行动，而 act_no_explore 是为了评分设计的，每次一定会采取 Q 最大的行动。

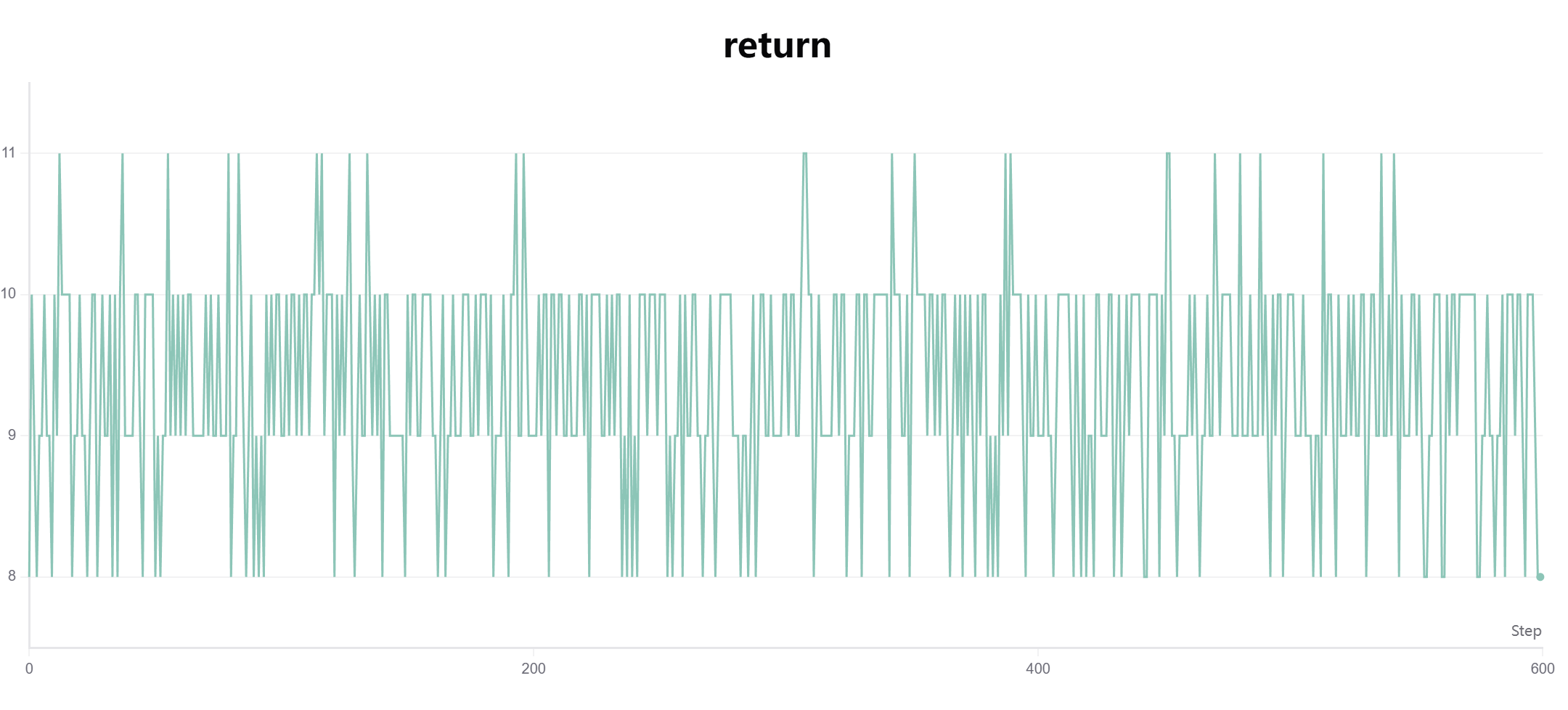
如果在训练过程使用 act_no_explore，则只会走以前的老路子，不断强化错误的观念。实验结果里得分情况极差，最高分只有 11 分（相比之下，正常最高分为得分上限 500 分）：

21:26 2025.12.05

目的：尝试调参

主要尝试调整 gamma 和 lr 两个参数