python编程练习---加权图最小路径（非固定起点）

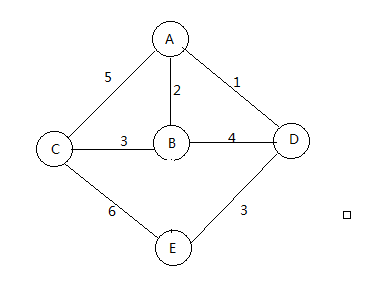
通过弗洛伊德(floyd)算法，可以计算出任意点到任意点的最短距离
floyd算法的核心点：
任意一个节点i到节点j的最小距离，一定是节点i到节点j的距离与节点i经过任意节点k到节点j的距离中最小的距离

所以，想要完成最小距离的计算，需要经过3层的循环遍历

首先将节点间的距离，用图来存储

graph = [
    [0, 2, 5, 1, math.inf],            #A到各个节点的距离，A到A为0，不可达的标记为无穷大
    [2, 0, 3, 4, math.inf],            #B到各个节点的距离
    [5, 3, 0, math.inf, 6],            #C到各个节点的距离
    [1, 4 , math.inf, 0, 3],           #D到各个节点的距离
    [math.inf, math.inf, 6, 3, 0]      #E到各个节点的距离
]

进行循环遍历

num_nodes = len(graph)      #节点个数
for k in range(num_nodes):  #经过k节点
    for i in range(num_nodes):
        for j in range(num_nodes):
            graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])      #ij的距离，为ij与ik+kj中的最小值

print("最短路径:",  graph)
print('A到E最短：', graph[0][4])

最短路径: [[0, 2, 5, 1, 4], [2, 0, 3, 3, 6], [5, 3, 0, 6, 6], [1, 3, 6, 0, 3], [4, 6, 6, 3, 0]]
A到E最短： 4