【题解】N皇后问题
N皇后问题
题目
\(N\)皇后问题是指将 \(n\) 个皇后放在 \(n×n\) 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
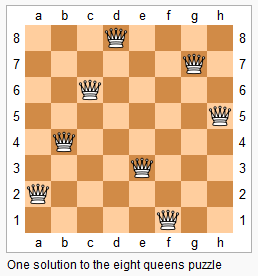
现在给定整数 \(n\),请你输出所有的满足条件的棋子摆法
输入格式
共一行,包含整数 \(n\)。
输出格式
每个解决方案占 \(n\) 行,每行输出一个长度为 \(n\) 的字符串,用来表示完整的棋盘状态。
其中 \(.\) 表示某一个位置的方格状态为空,\(Q\) 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
\(1≤n≤9\)
输入样例:
\(4\)
输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
题解1(全排列)
由于刚刚学了C++STL的全排列函数next_permutation,准备实战一下,所以不知道的小伙伴先看下:全排列函数next_permutation 或者看题解2。
全排列函数后\(a[i] = j\)相当于在第\(i\)行第\(j\)列有皇后,有效的帮我们解决了皇后不在同一行,同一列的问题。但是还不能同一对角线还没有判断,那么怎么解决呢?
在平面上的直线,对于问题,我们可以将其分为两种:
- \(y = x + b\)
- \(y = -x + b\)
由于一条斜线上,所以斜率要么为1要么为-1,而在同一斜线上的判定就变为:在坐标轴上的截距相同,即b相同
将两种关系转化为:
- \(b1 = y - x + n\)
- \(b2 = y + x\)
这里需要注意了,\(b1\)可能会存在负数,所以需要在后面加n保证映射为正数!
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <unordered_map>
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 100;
int a[N]; // i的位置存储j表示:第i行第j个位置有皇后
int n;
int b1[N], b2[N]; // 可以用数组存储哈希
void print()
{
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= n; j ++ )
{
if (a[i] == j) cout << 'Q';
else cout << '.';
}
cout << endl;
}
}
int main()
{
IOS;
cin >> n;
// 全排列必须升序, 先初始化数组
for (int i = 1; i <= n; i ++ ) a[i] = i;
// 枚举全排列, 这样就可以保证皇后行和列不同
do
{
vector<int> b1(N), b2(N); // 存储截距
//memset(b1, 0, sizeof b1), memset(b2, 0, sizeof b2);
bool vaild = true;
for(int i = 1; i <= n; i ++ )
{
if (++ b1[i - a[i] + n] > 1 | ++ b2[i + a[i]] > 1) // 如果斜率不是第一次出现
{
vaild = false;
break;
}
}
if (vaild)
{
print();
cout << endl;
}
} while (next_permutation(a + 1, a + n + 1));
return 0;
}
有人会说unordered_map可不可以,不可以,unordered_map会超时,虽然它有时候很方便,但是一定要尽量少用,它的查找并不一定是O(1),而vector比较优秀,在测试上没有被卡过hh,所以建议如果是数字哈希的话建议用数组模拟,比前两种都快!
题解2(dfs)
按照每个格子去搜索,有两种思路。
一种是先遍历列(或行),判断列末,行增加一,因为每次dfs到的点代表我们已经选择它,如果行不加一则会导致死路不通的情况。
另一种也是先遍历列(或行),此种方法如果列越界直接返回,通过枚举行的数值来进一步dfs,避免了上种方法死路的情况。
one:
#include <iostream>
#include <algorithm>
#include <cstring>
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 10;
char g[N][N];
bool col[N], row[N], dg[N*2], udg[N*2]; // 注意数组一定要开足够大
int n;
void print()
{
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < n; j ++ )
{
cout << g[i][j];
}
cout << endl;
}
cout << endl;
}
void dfs(int x, int y, int k)
{
g[x][y] = '.'; // 每个格子赋初值
if (k > n) return; // 如果已经枚举n个
if (y == n) y = 0, x ++ ; // 枚举完列则需要重新从下一行开始
if (x == n) // 当x枚举完才能进一步判断
{
if (k == n) // 如果已经枚举n个
{
print();
}
return;
}
dfs(x, y + 1, k); // 枚举递归列
if (row[x] || col[y] || dg[x + y] || udg[x - y + n]) return;
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
g[x][y] = 'Q';
dfs(x, y + 1, k + 1);
g[x][y] = '.';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
}
int main()
{
IOS;
cin >> n;
dfs(0, 0, 0);
return 0;
}
two:
#include <iostream>
#include <algorithm>
#include <cstring>
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 10;
char g[N][N];
bool col[N], row[N], dg[N*2], udg[N*2]; // 注意数组一定要开足够大
int n;
void print()
{
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < n; j ++ )
{
cout << g[i][j];
}
cout << endl;
}
cout << endl;
}
void dfs(int u)
{
if (u == n)
{
print();
return; // 如果已经枚举n个
}
for (int i = 0; i < n; i ++ )
{
if (col[i] || dg[i + u] || udg[i - u + n]) continue;
col[i] = dg[i + u] = udg[i - u + n] = true;
g[u][i] = 'Q';
dfs(u + 1);
// 回溯
g[u][i] = '.';
col[i] = dg[i + u] = udg[i - u + n] = false;
}
}
int main()
{
IOS;
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
第二种比第一种快一点点,所以建议顺序遍历所有二维数组的时候优先考虑枚举x,在循环枚举y。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号