digital fundamentals

chapter 1 digital concepts

digital and analog quantities

an analog quantity is one having continuous values. a digital digital quantity is one having a discrete set of values.

binary digits

positive logic: HIGH=1;LOW=0;

negative logic: HIGH=0;LOW=1;

logic levels

in a practical digital circuit, however, a high can be any voltage level between a specified minimum value and a specified maximum value.likewise, a low can be any voltage level between a specified minimum value and a specified maximum value.

no overlap(重叠)

digital waveforms

positive-going pulse: rising edge(leading edge), falling edge(trailing edge)

negative-going pulse:rising edge(trailing edge), falling edge(leading edge)

rise time [fall time]: 10% of the pulse amplitude (height from baseline) to 90%

pulse width: between 50% points

duty cycle(占空比)=pulse width/ the period (T).

chapter 2 number system, operations, and codes

decimal numbers

binary numbers:  the weight

binary-to-decimal conversion

decimal-to-binary conversion:

sum- of- weights method----9=8+1=2^3+1

repeated division- by- 2 method----短除法逆序

12/2=6......0

  6/2=3......0

  3/2=1......1

  1/2=0......1

12=1100(B)

converting decimal fraction to binary

0.3125x2=0.625……0

  0.625x2=  1.25……1

  0.25  x2=  0.50……0

  0.50 x2=  1.00……1

(个位)0.3125=.0101(B)

1’s and 2’s complements of binary numbers

finding the 1’s complement: 10110010---->01001101

finding the 2’s complement:

2’s complement=(1’s complement)+1: 10110010---->01001101+1=01001110

signed numbers

a 0 sign bit indicates a positive number, and a 1 sign bit indicates a negative number.

the decimal value of signed numbers

2’s complement

-2^7  2^6  2^5  2^4  2^3  2^2  2^1  2^0

  1       0      1     0      1     0      1      0

=-128+32+8+2=-86

10101010---->11010101+1=11010110=-(64+16+4+2)=-86

range of signed integer numbers that can be represented

range=-(2^(n-1))to (2^(n-1)-1)

floating – point numbers

sign

mantissa: represents the magnitude of the number

exponent: represents the number of paces that the decimal point (or binary point ) is to be moved.(指数)

single-precision  -->s(1bit)—exponent(8    bits)—mantissa(23 bits)    [32 bits]

double-precision—>s(1 bit)—exponent(11 bits)—mantissa(52 bits)    [64 bits]

there are 24 bits(single precision) in the mantissa because in any binary number the left-most bit is always  a 1. therefore , this 1 is understood to be there although it does not occupy an actual bit position.

1011010010001=1.011010010001x 2^12

s=0,e=10001011=139=127+12,mantissa=01101001000100000000000

exponent-127

arithmetic operations with signed numbers

addition

both numbers positive: 00000111+00000100=00001011—>7+4=11

positive number with magnitude larger than negative number:00001111+11111010=1  00001001 (15-6=9)

negative number with magnitude larger than positive number:00010000+11101000=11111000  (16-24=-8)

both numbers negative:11111011=11110111=1  11110010 (-5-9=-14)

overflow condition(only occur when both numbers are positive or negative )

01111101+00111010=10110111 (125+58=183)

subtraction

  the sign of a positive  or negative number is changed by taking 2’s complement

00000100(+4) 11111100(-4)

multiplication

the partial method is perhaps the more common one because it reflects the way you multiply longhand.

step1—sign

step2—change any negative number to true(uncomplemented) form.

step3—generate the partial products(only the magnitude bits are used in these steps)

step4—add each partial products

step5—if sign that  was determined is negative, 2’s complement,if positive ,attach the sign bit to the product.

division

dividend / divisor =quotient

subtract the divisor

hexadecimal numbers

binary code decimal

binary coded decimal(BCD) is a way to express each of the decimal digits with a binary code. there only ten code groups in the BCD system.

the 8421 Code

  when we refer to BCD, we always mean the 8421 code unless otherwise stated

1010,1011,1100,1101,1110,1111 are invalid codes

0010 0011+0001 0101=0011 1000=23 + 15= 38

0001 0110+0001 0101=0010 1101=0010 1011+0110(6)=0011 0001=16+15=31

digital codes

the gray code(unweighted)

feature:it exhibits only a single bit change from one code word to the next in sequence.

binary-to- gray code conversion

going form left to right, add each adjacent( 相邻的) pair of binary code bits to get the next gray code bit. discard carries(丢弃进位)

the most significant bit (left-most) in the gray code is the same as the corresponding MSB in the binary number

(符号位相同,与前一位的摩尔和得到格雷码的bit)

1+0+1+1+0 binary

1  1  1  0  1 gray

gray-to-binary conversion

1 1 1 0 1 gray code

1 0 1 1 0 binary code( 差分 )

alphanumeric codes

ASCII

hamming code

data bits : d  ;    parity bits: p

2^p>= d+p+1

chapter3 logic gates

the inverter:---->x=A’

not circuit performs the operation called inversion or complementation

the and gate---->x=AB

the or gate---->x=A+B

the nand gate---->x=(AB)’

the nor gate---->x=(A+B)’

the exclusive-or gate:x=AB’+A’B 异或

the exclusive-nor gate:x=AB+A’B’ 同或

chapter 4 boolean algebra and logic simplification

laws of boolean algebra

commutative laws:

A+B=B+A

AB=BA

associate laws

A+(B+C)=(A+B)+C

A(BC)=(AB)C

distributive law

A(B+C)=AB+AC

rules of boolean algebra

A+0=A    A+1=1

A .0=0     A .1=A

A+A=A    A+A’=1

A .A=A    A .A’=0

A’’=A

A+AB=A    A+A’B=A+B

(A+B)(A+C)=A+BC

Demorgan’s theorems

(XY)’=X’+Y’

(X+Y)’=X’Y’

standard form of boolean expression

The sum-of-products(SOP)  form

AB+ACD

the products-of-sums(POS)  form

(A’+B)(A+B’+C)

converting standard SOP to standard POS

step1—>evaluate each product term in the SOP expression. That is , determine the binary numbers that represent the product terms.

step2—>determine all of the binary numbers not included in the evaluation in step1

step3—>write the equivalent sum term for each binary number from step2 and express in POS form

AB’+A’B---->[10] [01]

(A+B)(A’+B’)---->[00] [11]

SOP[A---->1]

POS[A---->0]

also KARNAUGH map and truth tables

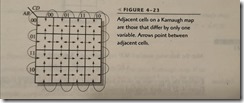
the KARNAUGH map(卡诺图)

the Quine-McClusky method

00 01 11 10

cell adjacency(相邻)

mapping a standard SOP expression

A’B’C’---->000---->1

mapping a standard POS expression

(A+B+C)---->000---->0

simplification 

1.a group must contain either 1,2,4,8, or 16 cells,which are all powers of two.

2.each cell in group must be adjacent to one or more cells in  that same group . but all cells in the group do not have to be adjacent to each other.

3.always include the largest possible number of 1s in a group  in accordance with rule 1.

seven segment display

chapter 5 combinational logic analysis

basic combinational logic circuits

and-or logic

and-or-invert logic

exclusive-or  logic(异或)

exclusive-nor logic

chapter 6 functions of combinational logic

basic adders

the half-adder

the half-adder accepts two binary digits on its inputs and produces two binary digits on its outputs, a sum bit and a carry bit.

sum=AB’+A’B

C_out=AB

the full-adder

the full-adder accepts two input bits and an carry and generates a sum output and an output carry.

port: A,B,C_in in std_logic

        sum,C_out out std_logic

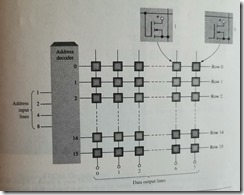
chapter 10 memory and storage

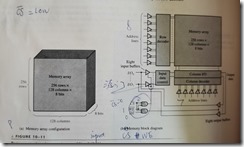
the address depends on how the memory is organized into units of data

 

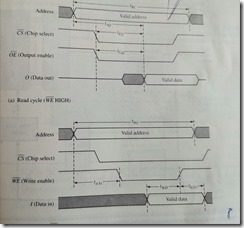
basic memory operations

read/write

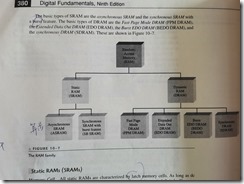
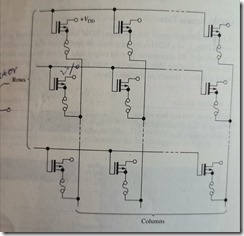
RAM

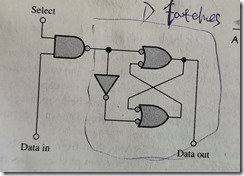
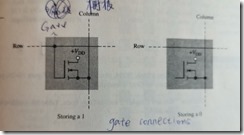
SRAM

tristate buffer 三态门

cycle

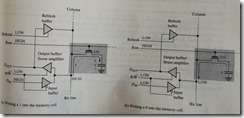
DRAM

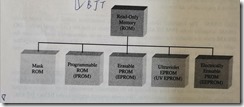
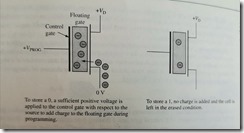
ROM

PROM

fusible links

flash

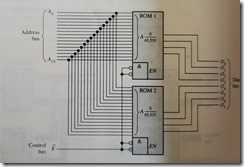
memory expansion

FIFO