slam(2)---李群、李代数

通过李群——李代数间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方式。

一、群

群（ Group）是一种集合加上一种运算的代数结构。记作G = (A; ·)，满足一下条件。

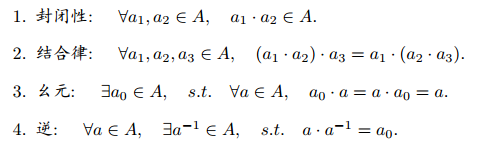
李群是指具有连续（光滑）性质的群

二、李代数

李代数描述了李群的局部性质。李代数由一个集合 V，一个数域 F 和一个二元运算 [;] 组成，称 (V; F;[;]) 为一个李代数，记作 g

满足一下条件：

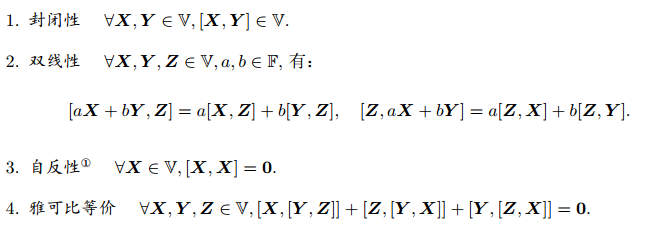
二元运算被称为李括号

 三、李代数so(3)

SO(3) 对应的李代数是定义在 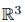上的向量，我们记作 ϕ。每个ϕ都对应一个反对称矩阵。

　　

两个向量 ϕ1; ϕ2 的李括号：

　　

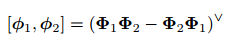
 可以说，so(3) 的元素是 3 维向量或者 3 维反对称矩阵。

　   

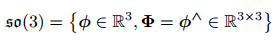
so(3)和SO(3)的关系可以由指数映射表示：

　　 

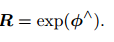
 三、李代数se(3)

se(3) 位于 空间中:

每个 se(3) 元素记作 ξ，它是一个六维向量。前三维为平移，记作 ρ；后三维为旋转，记作 ϕ，实质上是 so(3) 元素‹。

　　

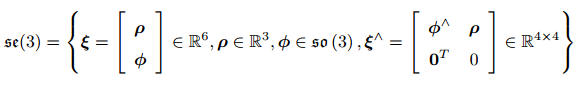
使用 ^ 符号，将一个六维向量转换成四维矩阵，但这里不再表示反对称：

　　　

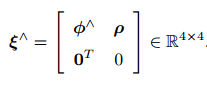
使用 ^ 和 _ 符号来指代“从向量到矩阵”和“从矩阵到向量”的关系。

李代数 se(3)的李括号：

　　　　

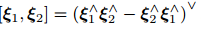
se(3)和Se(3)的关系可以由指数映射表示：

                 =

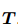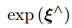
四、指数与对数映射

1、 SO(3)上的指数映射

so(3)--->SO(3):

　       　

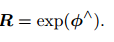
 ϕ 是三维向量，我们可以定义它的模长和它的方向，分别记作 θ 和 a，于是有 ϕ = θa, a 是一个长度为 1 的方向向量。

　　　

　　　  　　　　

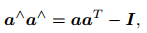
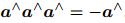
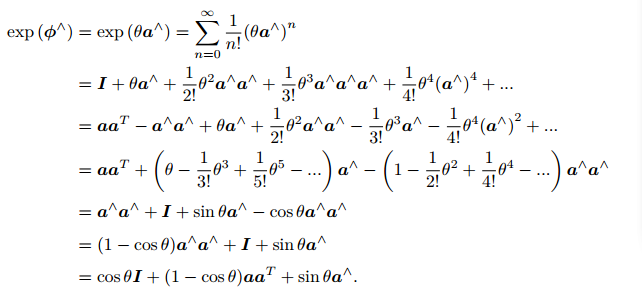
上式就是罗德里格斯公式(旋转向量  ---->   旋转矩阵)。

 

反之， SO(3)--->so(3):

　　　　

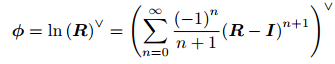
指数映射只是一个满射。这意味着每个 SO(3) 中的元素，都可以找到一个 so(3) 元素与之对应；

但是可能存在多个 so(3) 中的元 素，对应到同一个 SO(3)。

 

2、 SE(3)上的指数映射

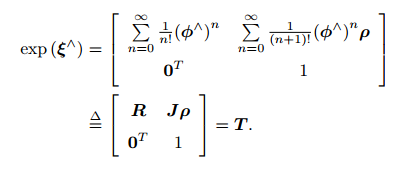
左上角的 R 是SO(3) 中的元素,J 则可整理为（设 ϕ = θa）：

　　

 

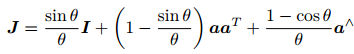
平移部分经过指数映射之后， 发生了一次以 J 为系数矩阵的线性变换。

 

3、SO(3); SE(3); so(3); se(3) 的对应关系

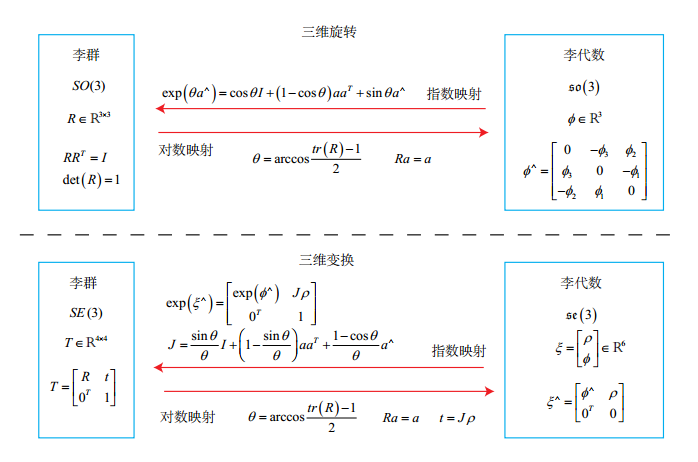
四、李代数求导与扰动模型

1、 BCH (Baker-Campbell-Hausdorff)

两个李代数指数映射乘积的完整形式,有BCH公式刻画。

　　展开式的前几项： [] 为李括号

　　　　

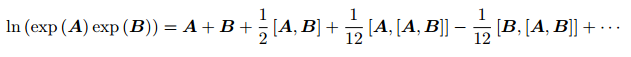
SO(3) 上的李代数 ln(exp(ϕ^ 1) exp(ϕ^ 2))_，当 ϕ1 或 ϕ2 为小量时，BCH近似表达为：

　　　　　

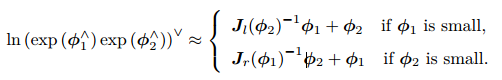
左乘(左乘一个 微小旋转矩阵)为例，左乘 BCH 近似雅可比  。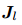

　　　　　　

　　　　　　　　　　　

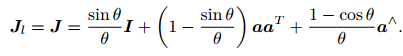
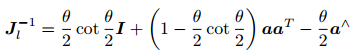
BCH，表达了李群乘法 和 李代数加法的关系。

　　　　　　

 

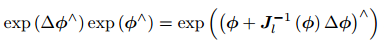
同理对于SE(3),BCH 近似为:

　　　　

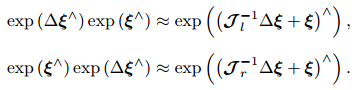
经常会构建与位姿有关的函数，然后讨论该函数关于位姿的导数，以调整当前的估计值。然而， SO(3); SE(3) 上并没有良好定义的加法，它们
只是群。如果我们把 T 当成一个普通矩阵来处理优化，那就必须对它加以约束。

从李代 数角度来说，由于李代数由向量组成，具有良好的加法运算。因此，使用李代数解决求导 问题的思路分为两种：

2、 李代数求导

以SO(3)为例：

　　　　

           

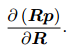
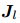比较复杂。

 

3、扰动模型(左乘)

左扰动 ∆R 对应的李代数为 φ。然后，对 φ 求导:

　　

        

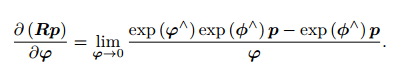
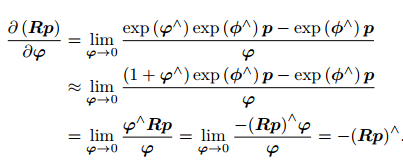
4、SE(3)上的李代数求导

给 T 左乘一个扰动 ∆T = exp(δξ^)，我们设扰动项的李代数为 δξ = [δρ; δϕ]T

　　

⊙它把一个齐次坐标的空间点变换成一个 4 × 6 的矩阵