提高RM-MEDA局部学习（IRM-MEDA）

IRM-MEDA：Improved RM-MEDA with local learning  

原文：https://link.springer.com/article/10.1007/s00500-013-1151-2

1.摘要

为了提高基于规则模型的多目标分布估计算法(RM-MEDA)，基于分布估计的典型多目标优化算法，的收敛速度和收敛精度，本文提出了一种局部学习算法，RM-MEDA采用了一种基于模型的方法来生成新的解决方案，但是，这种方法在人口没有明显的规律性时很容易生成差解。 为了克服这一缺点，我们提出的方法在原有的RM-MEDA的基础上增加了一种新的解决方案生成策略，即局部学习。局部学习是通过在邻域中抽取从父母群体中精英解决方案的解来产生解决方案的。由于在邻域中很容易找到精英解，局部学习可以得到一些有用的解决方案，帮助种群快速、准确地收敛。

2.介绍

多目标优化问题(MOP)中的目标往往是相互冲突的，这些目标不能同时通过一个单一的解来优化。因此，需要找到一组近似于Pareto最优集(PS)的解，供决策者选择。

以Pareto排序和适应度共享为基础，采用基于Pareto排序和适应度共享的选择机制来保持多样性，构成了开拓性的多目标方法。

传统的MOEAs没有从以前的搜索中提取全局统计信息并用来指导进一步搜索的机制。因此，传统的MOEAs通常能力有限。

根据优化问题变量间相互作用的建模方法，将EDAS划分为三个不同的类。

在第一类中，假设一个问题的参数之间的关系是独立的。因此，解的概率分布可以被认为是独立的单变量概率的乘积。

与传统的MOEA相比，EDAS将更多的人口分布信息考虑在内，而不是个别的本地信息。

EDAS与局部搜索或精英策略相结合成为近年来多目标优化的研究热点。

3.相关工作

RM-MEDA：在基于模型的繁殖过程中，利用局部PCA算法首先将种群P(t)划分为k个不相交聚类，然后是方程(5)的模型为每个集群进行构建。最后，从这些模型中抽取新的解决方案。

由于Pareto set是分段的（m-1）维的流型，我们希望种群中的点尽可能逼近理想Pareto Set，并均匀分布在理想set的周围。该算法将种群中的个体看作随机向量ξ∈Rn的独立观测数据，其中占ξ属于Rn，n是决策变量的维度，这些观测量的质心正好构成Pareto Set。故ξ可描述为：
ξ= ζ+ ε
上式中的ζ均匀分布在m-1维流形周围，是算法需要建立的分布模型。ε是一个n维的均值为零的噪声向量,表示种群中的个体在流型周围的随机扰动，具体情况如下：

RM-MEDA：https://blog.csdn.net/u014119694/article/details/77281388

4.RM-MEDA with local learning

4.1动机

基于PS规则，RM-MEDA建立了概率分布，然后从模型中抽取样本以产生新的解决方案。当规律明显时，它效果很好。然而，在迭代开始时，当种群没有明显的规律性时，得到的新解总是很差的。这使得种群收敛性差。导致收敛性差的原因之一是基于模型的抽样没有直接使用高质量解的位置信息。 为了克服这个缺点，我们在原有的RM-MEDA的基础上增加了一种新的解决方案生成策略，即局部学习。本地学习通过从母体人群的精英解决方案的邻域中采样一些解决方案来产生解决方案。由于在一个很好的解的邻域内寻找一些有前途的解是容易的，因此局部学习可以得到一些有用的解，以帮助种群获得快速而准确的收敛。

4.2算法

这一部分将讨论IRM-MEDA的框架。首先，图3列出了IRM-MEDA的主要步骤，其中N是种群规模。θ是一个比例系数，r是长度系数P(T)和Q(T)分别代表父代种群和后代种群。BR表示解X的邻域，定义如下：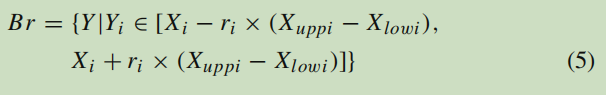

首先，从具有竞赛选择的父种群P(T)中选择θ×N高质量的解。在第一次迭代中，应用了nsga-ii中的快速非支配排序方法对父种群进行排序。具有较低非支配前沿的解将被设置一个较小的数字。而数字较小的个体在比赛选择中有更高的优先权。在其余的迭代中，最后一次迭代中进行NDS选择之后，对父种群进行非支配排序。在此基础上进行了比赛选择。然后，从这些精英解的邻域取样个体。为了在勘探和开发之间找到平衡，本研究定义了非支配解的邻域小于支配解。这样，就可以从非支配解的邻域中抽取优秀解来提高收敛性。并且从主支配的邻域采样的解可以增加多样性。最后，这些个体被合并到后代群体Q(t)中。此外，如果由本地学习复制生成的解决方案的一个元素超出了可行的决策空间，我们只需将其值重置为在可行空间内随机选择的值。

基于规则模型的多目标估计分布算法。RM-MEDA
step0.初始化： 初始化种群Pop(t)中的每个个体对应的目标函数值F，令t=0；

step1.停止条件： 如果停止满足条件，停止并返回Pop(t)中的Pareto解集和对应的目标函数向量F；

step2.建立模型： 根据种群Pop(t)中的解的分布建立一个概率模型；

step3.产生新解： 从建立好的模型中选择一个新的解集Q，评价Q中的每一个解的F值；

step4.排序选择： 从Pop(t)∪Q中选取N个个体作为新的种群Pop(t);

step5.： 令t=t+1，转步骤1
该算法就是根据解集构造模型然后又从模型中构造新的解集，然后同该代原始解结合生成下一代解。

PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征

IRM-MEDA
step0.初始化： 初始化种群Pop(t)中的每个个体对应的目标函数值F，令t=0；
step1.分类：对Pop（t）进行快速非支配排序
step2.局部学习繁殖（进化）：
    1）从Pop（t）中进行选择优秀的个体X
    2）如果X是非支配解则让长度系数设为r，否则设为2r
    3）从Br中选取样本的个体的解放入Q(t)中
    4）返回到1）知道学习的解有θ*N个
step3.建立模型： 根据种群Pop(t)中的解的分布建立一个概率模型；

step4.产生新解： 从建立好的模型中选择(1-θ)*N个加入Q(t)，评价Q(t)中的每一个解的F值；

step5.排序选择： 从Pop(t)∪Q(t)中选取N个个体作为新的种群Pop(t)[用非支配+拥挤距离],
令t=t+1；
step6.停止条件： 如果停止满足条件，停止并返回Pop(t)中的Pareto解集和对应的目标函数向量F，
否则转到step2；
该算法就是根据较好的解的进行局部学习产生一部分新解,再通过解集构造模型然后又从模型中构造剩下新的解集，然后同该代原始解结合生成下一代解。

下图是一个例子

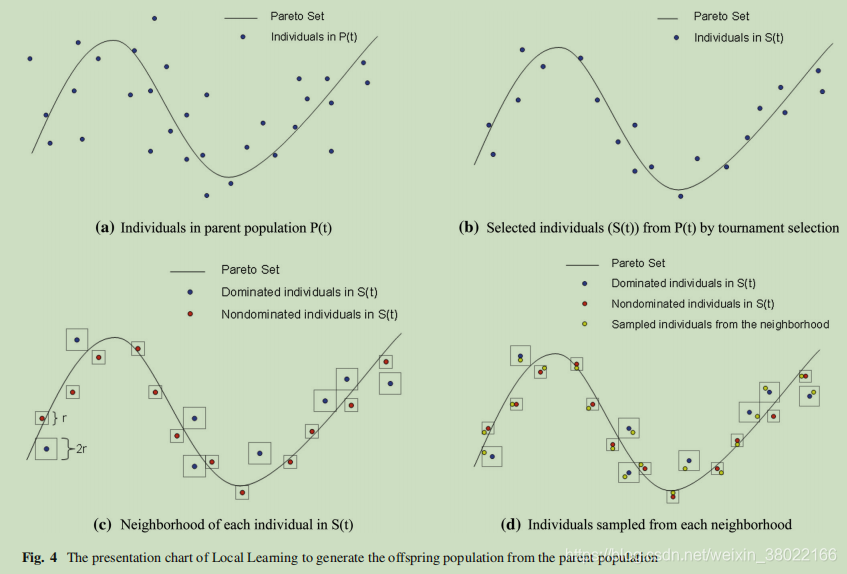
基本思想的说明。在一个成功的MOEA中，单个的解决方案应该分散在决策空间的PS上。

5.实验

在IRM-MEDA中，在局部学习复制过程中需要固定两个参数。比例系数θ表示局部学习产生的解的数目，长度系数r表示解的邻域大小。地方学习可以帮助人们提前达到规律，并能更快地收敛。然而，如果选择了不合适的θ和r，种群可能会陷入局部最优状态，而局部学习可能没有意义。因此，正确选择θ和r是很重要的。因此，我们为实验中的所有实例设置了θ=0.4和r=0.4。