KD树

参考：
1. 算法训练营6.1
简介：
1. 名称：KD树（K-Dimension tree）。
2. 本质：是二叉树，但是是二叉搜索树的扩展，用于多维空间数据的搜索（范围搜索和最近邻搜索），提高搜索效率。
3. 一些abstract：BST、AVL、Treap和伸展树等二叉搜索树的节点存储的都是一维信息。而多维数据需要一个纬度Di，在维度Di上进行大小比较。比如二维平面上的点A(2, 4)和B(5, 3)，按照第一维度比较则A<B，二按照第二维度比较，则A>B。
操作：
1. 创建KD树：
  
  KD树中的每个节点都对应着K维空间中的一块超矩形区域，可以省去大部分的搜索工作。
  
  对K维数据划分时，需要考虑两个问题：
  1. 选择哪个维度划分？
  2. 选择哪个点做父亲，才能让其左右子树大小大致相等。
  先解决第一个问题：选择哪一维作为分辨器。KD树可以根据不同的用途选择不同的分辨器，常见的是轮转法和最大方差法：
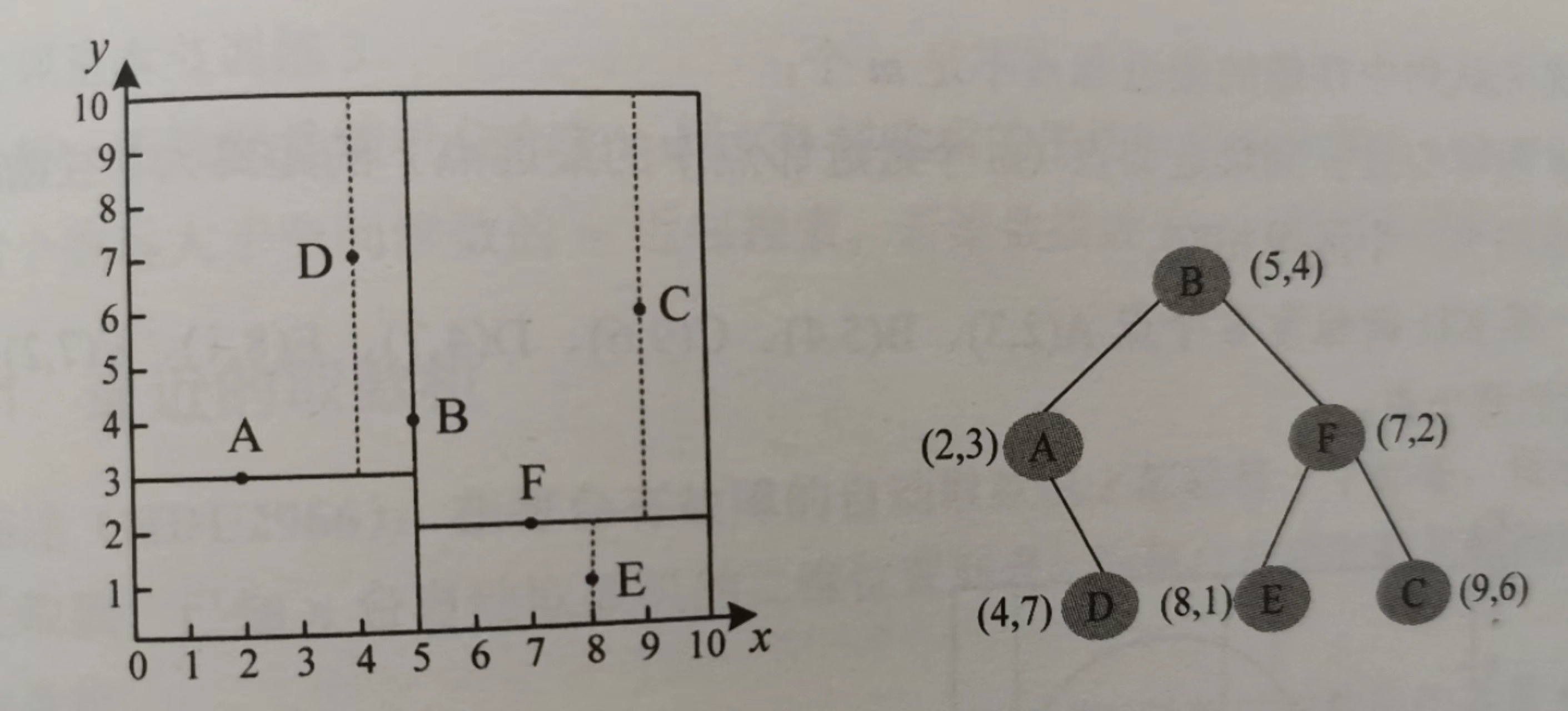
  1. 轮转法：按照维度轮流作为分辨器，对于二维数据(x, y)，第一层按照x划分，第二层按y划分，然后第三层又按x划分...
    
    第一层的B是因为在所有的点中，B的横坐标在中间，所以B做根，相当于竖着切了一刀，左子树就是在左边的A和D，右子树就是C、E、F。
    
    第二层中，左子树中A在中间，所以A做根，按照y划分，D是A的右儿子；右子树中，F的纵坐标在中间，E的纵坐标更小，所以在F的左子树，C的纵坐标大于F，所以在F的右子树。
  2. 最大方差法：若数据在维度Di方差最大，则选择维度Di作为分辨器。因为方差代表数据的分散程度，越大就越容易划分。然后第二层再按第二大的方差选，...，直到循环一轮，然后又按照方差最大的维度切。
  然后第二个问题，每次选中位数作为划分点，就像上面一样。可以采用STL的nth_element(begin, begin+k, end, compare)函数，该函数使得[begin, end)区间内的第k小的元素处于第k个位置，左边的元素均不超过这个值，右边的元素都不小于这个值，但并不保证别的元素有序，复杂度O(end-begin)。
```
 const int N = 100100;
 int idx;  // idx表示按照idx维排序
 struct Node {
   int x[2];
   bool operator < (const Node &b) const {
     return x[idx] < b.x[idx];
  }
 }a[N];
 
 struct KD_Tree {
   int sz[N << 2];  // 类似线段树的操作
   Node kd[N << 2];  // 同上
   void build(int rt, int l, int r, int dep) {  // 当前在rt节点，解决[l, r]区间的切分问题，深度为dep
     if (l > r) return;
     int mid = l + r >> 1;
     idx = dep % k;  // 用轮转法
     sz[rt] = 1;
     sz[rt << 1] = sz[rt << 1 | 1] = 0;
     nth_element(a + l, a + mid, a + r + 1);  // [l, r+1)
     kd[rt] = a[mid];  // 中间节点当成根
     build(rt << 1, l, mid - 1, dep + 1);  // 左子树 [l, mid - 1] dep + 1深度
     build(rt << 1 | 1, mid + 1, r, dep + 1);  // 右子树 [mid + 1, r] dep + 1深度
  }
 }KDT;
```
2. m近邻搜索：
  
  KD树支持查询距离给定目标点p（不一定在树上）最近邻的m个点，从根节点出发，向下递归。当点p的当前行的维度坐标小于树根时，则在左子树中查询，否则在右子树中查询，在查询过程中使用优先队列（大根堆）存储最近的m个点，当存在某一个点q比大根堆中的最远点距离p更近时，pop之后让q入队。
  
  什么情况下放到堆里呢？首先只有回溯到这个点的时候，即找完一半子树之后才考虑将这个点放入堆中，其次：
  1. 堆没满。
  2. 比根顶点更近。
  然后就是判断到底去不去另一半子树查找，以下两种情况中，需要继续在当前划分点的另一区域查询（指查询完了一侧到底应不应该查另一侧）：
  1. 当前大根堆中存储的点不足m个，这显然随便找点就可以放进去，肯定要找一下。
  2. 以p为球心，以p到根顶的点的距离为半径的“球体”和另一区域相交，那就是有机会有更小距离的点，所以也要找一下。
  下面举个例子：
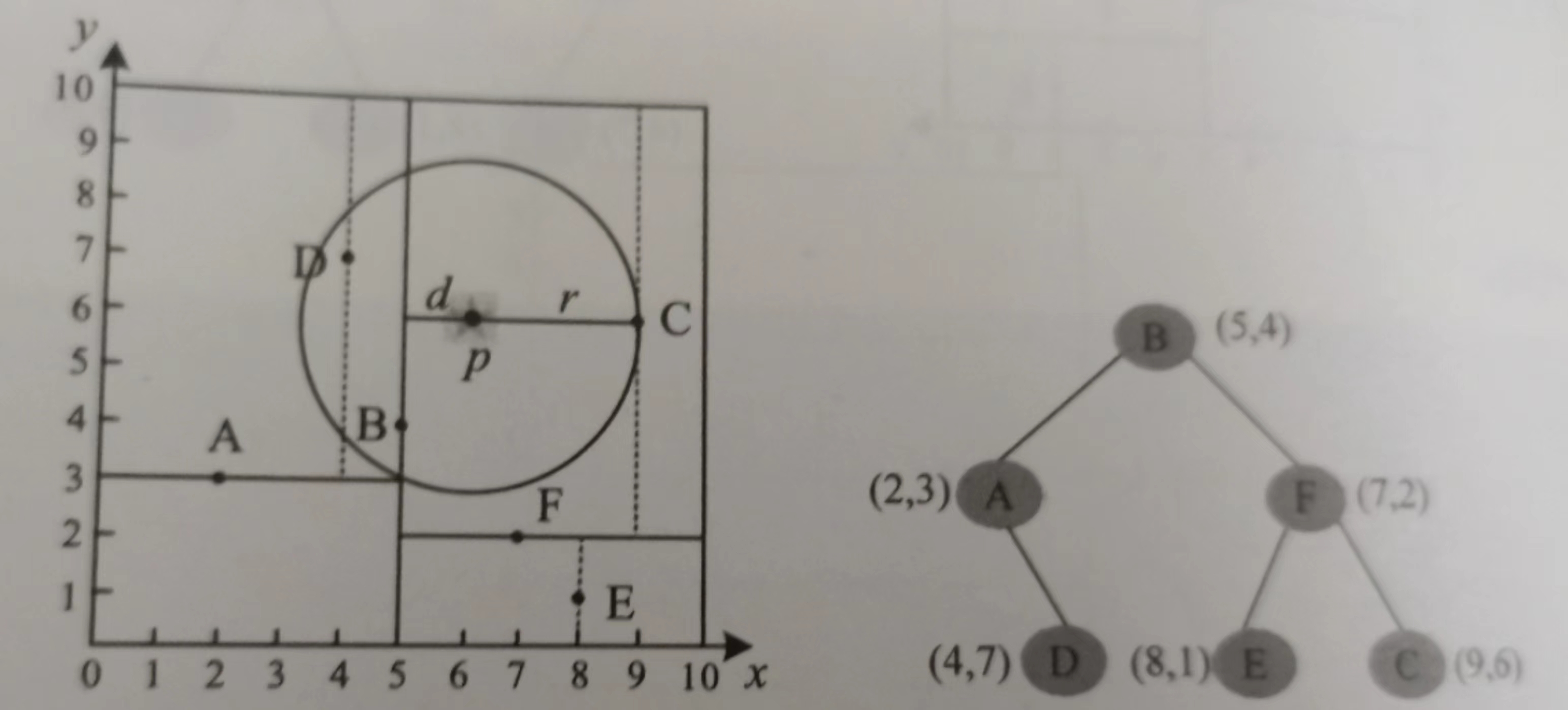
  1. 还是这个图，先看一下p(6, 6)的位置，想要找最近的两个点，初始位置在B。
  1. 因为p的x坐标大于B，所以先去右边找，到了F。
  2. p的y坐标大于F，所以去右边找，到了C。
  3. 因为p的x坐标小于C，所以去左边找，哎，为空，回溯到C，因为堆未满，于是将C放进大根堆。
  4. 因为大根堆里只有一个东西，小于二，所以去C的右子树找，发现也为空，于是回溯到F，因为堆未满，于是将F放进大根堆，此时根顶为F。
  5. 半径为|pF|的圆和F的下半部分（另一区域）有相交的部分，所以去F的左子树找，到了E。
  6. 因为E的x坐标大于p，所以去E的左子树找，为空，回溯到E，发现|Ep|>|Fp|，于是不管E，也不管E的右子树，回溯到B。
  7. 因为|Bp|<|Fp|，即小于根顶的距离，于是F出队，B入队，现在根顶为C，同时因为这个圆和B的左子树代表区域有公共部分，所以需要去B的左子树，于是到了A。
  8. 因为A的y坐标小于p，所以去A的左子树，为空，回溯到A，A比根顶还远，于是A不能进队，同时因为以|Cp|为半径的圆和A的右子树（另一区域）有交点，所以需要去A的右子树找，于是到了D。
  9. D的x坐标小于p，所以需要去D的右子树，为空，回溯到D。
  10. 发现D的距离小于堆顶C，于是C出队，D入队，此时堆顶为D。
  11. 又因为以|Dp|为半径的圆和另一区域即D的左子树的区域有公共部分，所以需要去D的左子树看一下，为空，返回，回溯到A，因为A已经判断过了，回溯到B，B判断过了，则运行结束。
  最终结果为B和D。
  
  （不知道是为什么的）结论：若数据是随机分布的，则KD树搜索的平均时间复杂度是O(logn)，KD树适用于数据元素个数院小于空间维数的m近邻搜索，如果维数接近于n，则效率接近于线性扫描。
  
  代码可能在例题里（x

例题：代码均仅为参考，重点领悟精神！！！ce、wa了概不负责！！！

（基础的代码编写）（HDU2966），T组测试样例，每一组给若干个二维点坐标，让输出对于每个节点，离它最近的点的距离平方（不算自己）。没有点重合的情况。

 #define sq(x) (x)*(x)
 typedef long long ll;
 
 const ll inf = 1e18;
 const int k = 2;
 const int N = 100000 + 10;
 int idx;
 
 struct Node {
   int x[2];
   bool operator < (const Node &b) const {
     return x[idx] < b.x[idx]
  }
 }a[N], q[N];
 
 ll dis(Node p, Node q) {
   ll ret = 0;
   for (int i = 0; i < k; i++) {
     ret += sq((ll)p.x[i] - q.x[i]);
  }
   return ret ? ret : inf;  // 不能是自己，是自己直接变成inf淘汰掉
 }
 
 void build(int rt, int l, int r, int dep) {
   if (l > r) return;
   sz[rt] = 1;
   sz[rt << 1] = sz[rt << 1 | 1] = 0;
   int mid = l+r >> 1;
   idx = dep % k;
   nth_element(a + l, a + mid, a + r + 1);
   kd[rt] = a[mid];  // kd节点存一下，方便查找，q数组存的才是真的值，a的已经被打乱了
   build(rt << 1, l, mid - 1, dep + 1);
   build(rt << 1 | 1, mid + 1, r, dep + 1);
 }
 
 ll ans = inf;
 // 只是问最近 不用优先队列 每次都要初始化为inf～
 void query(int rt, int l, int r, int dep, Node p) {  // 查询点p到最近点的平方距离
   if (l > r) continue;
   int mid = l + r >> 1;
   int dim = dep % k;
   ll distance = dis(kd[rt], p);
   if (distance < ans) {
     ans = distance;
  }
   ll dis_dim = sq((ll)p.x[dim] - kd[mid].x[dim]);  // 先提前算出来我这个距离，如果发现最远（因为只问一个点，所以最近即最远），则要去另一边搜索。
   if (p.x[mid] < kd[mid].x[mid]) {
     query(rt << 1, l, mid - 1, dep + 1, p);
     if (dis_dim < ans) {  // 如果最远的圆比这个按维算的距离（对应切分的区域）大，说明和切分的另一半有公共部分，所以应该查询另一半
       query(rt << 1 | 1, mid + 1, r, dep + 1, p);
    }
  }
   else {
     query(rt << 1 | 1, mid + 1, r, dep + 1, p);
     if (dis_dim < ans) {  // 如果最远的圆比这个按维算的距离（对应切分的区域）大，说明和切分的另一半有公共部分，所以应该查询另一半
       query(rt << 1, l, mid - 1, dep + 1, p);
    }
  }
 }

最后复杂度O(Tnlogn)

最近邻k维M点（HDU4347）。k（5），M（10），总点数N（50000），查询数t（10000）。

 typedef long long ll;
 typedef pair<ll, Node>PLN;
 
 priority_queue<PLN> que;  // 大根堆
 
 void queue(int rt, int m, int dep, Node p) {  // m点
   int (!sz[rt]) return;
   PLN tmp = PLN(0, kd[rt]);
   for (int j = 0; j < k; j++) {  // k维
 tmp.first += sq((ll)tmp.second.x[j] - p.x[j]);  // 求出距离
  }
   int lc = rt << 1, rc = rt << 1 | 1, dim = dep % k, flag = 0;
   if (p.x[dim] >= kd[rt].x[dim]) swap(lc, rc);  // 这样lc变量永远都是放的先搜索的一侧
   if (sz[lc]) query(lc, m, dep + 1, p);
   // 回溯之后判断是否加入
   if (que.size() < m) {  // 如果没满，直接放进去
     que.push(tmp);
     flag = 1;  // 同时也标记应该搜索另一侧
  }
   else {
     if (tmp.first < que.top().first) {  // 比最远的近 应该插入
       que.pop();
       que.push(tmp);
    }
     if (sq((ll)p.x[dim] - kd[rt].x[dim]) < que.top().first) {  // 圆形区域和另一半区域有公共部分
       flag = 1;  // 也应该搜索另一边
    }
  }
   if (sz[rc] && flag) query(rc, m, dep + 1, p);  // 应该搜索且不空
 }

复杂度O(tlogNmax(k, logM))（大概是这样子？？？反正很宽松就对了）。别忘了原题是不定组数据！！！

蚁巢（HDU5809），有N个蚁巢，没有两个蚁巢在同一个位置，所有蚂蚁遵守一些规律，蚂蚁在一个蚁巢时，会沿着直线走向距离当前蚁巢最近的蚁巢，如果有多个距离一样，会选择x坐标更小的，如果x坐标一样，会选择y坐标最小的。所有蚂蚁都不停地走，所有蚂蚁可以无限次访问同一个蚁巢，所有蚂蚁移动速度都相同，每次询问问从p、q两个蚁巢出发的两个蚂蚁，可不可以某个时间相遇。

通过你强大的第六感，应该能感觉到，最后不管什么样，蚂蚁都是会在两个蚁巢之间走来走去，这样早晚能遇到，也就是说我们可以把能走到这两个蚁巢的所有蚁巢都归为一类，就是用冰茶姬（x）啦～

也就是找到每个节点的最近的节点（x和y坐标的大小也要算在符号计算内），即稍微改一下KD树的判断大小的条件，然后还有一个注意的点是：判断覆盖要带上等号，因为可能出现原来的点在右侧，然后新的点在左侧的情况，带上等号才能更新，不然就略过了。代码几乎同第一题（除了上面提到的），这里略过～

posted on 2022-05-12 22:59 小染子阅读(183) 评论(0) 收藏举报