常用排序算法记录
一、前言
简单记录一下常用的算法排序,以便复习
二、快速排序
主要思想:
(1)在数据集之中,选择一个元素作为"基准"(pivot)。
(2)所有小于"基准"的元素,都移到"基准"的左边;所有大于"基准"的元素,都移到"基准"的右边。
(3)对"基准"左边和右边的两个子集,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。
代码实现:
function quickSort($arr){
$length = count($arr);
$arr_left = array();
$arr_right = array();
if($length <= 1){
return $arr;
}
$pivot = $arr[0];
for($i = 1 ;$i < $length; $i ++){
if($arr[$i] <= $pivot){
$arr_left[] = $arr[$i];
}else{
$arr_right[] = $arr[$i];
}
}
$arr_left = quick_sort($arr_left);
$arr_right = quick_sort($arr_right);
$arr = array_merge($arr_left,array($pivot),$arr_right);
return $arr;
}
$arr = array(2,1,4,5,3);
var_dump(quickSort($arr));
三、归并排序
主要思想:
主要是利用 分治法 ;
首先考虑下如何将二个有序数列合并。这个非常简单,只要从比较二个数列的第一个数,谁小就先取谁,取了后就在对应数列中删除这个数。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可。
归并排序,就是 将数组分成二组A,B,然后分别将A,B再分成两组,依次类推,当分出来的小组只有一个数据时,可以认为这个小组组内已经达到了有序,然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列,再合并数列就完成了归并排序。
步骤:
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
设定两个指针,最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
代码实现:
/**
* mergeSort 归并排序
* 是开始递归函数的一个驱动函数
* @param &$arr array 待排序的数组
*/
function mergeSort(&$arr) {
$len = count($arr);//求得数组长度
mSort($arr, 0, $len-1);
}
/**
* 实际实现归并排序的程序
* @param &$arr array 需要排序的数组
* @param $left int 子序列的左下标值
* @param $right int 子序列的右下标值
*/
function mSort(&$arr, $left, $right) {
if($left < $right) {
//说明子序列内存在多余1个的元素,那么需要拆分,分别排序,合并
//计算拆分的位置,长度/2 去整
$center = floor(($left+$right) / 2);
//递归调用对左边进行再次排序:
mSort($arr, $left, $center);
//递归调用对右边进行再次排序
mSort($arr, $center+1, $right);
//合并排序结果
mergeArray($arr, $left, $center, $right);
}
}
/**
* 将两个有序数组合并成一个有序数组
* @param &$arr, 待排序的所有元素
* @param $left, 排序子数组A的开始下标
* @param $center, 排序子数组A与排序子数组B的中间下标,也就是数组A的结束下标
* @param $right, 排序子数组B的结束下标(开始为$center+1)
*/
function mergeArray(&$arr, $left, $center, $right) {
//设置两个起始位置标记
$a_i = $left;
$b_i = $center+1;
while($a_i<=$center && $b_i<=$right) {
//当数组A和数组B都没有越界时
if($arr[$a_i] < $arr[$b_i]) {
$temp[] = $arr[$a_i++];
} else {
$temp[] = $arr[$b_i++];
}
}
//判断 数组A内的元素是否都用完了,没有的话将其全部插入到C数组内:
while($a_i <= $center) {
$temp[] = $arr[$a_i++];
}
//判断 数组B内的元素是否都用完了,没有的话将其全部插入到C数组内:
while($b_i <= $right) {
$temp[] = $arr[$b_i++];
}
//将$arrC内排序好的部分,写入到$arr内:
for($i=0, $len=count($temp); $i<$len; $i++) {
$arr[$left+$i] = $temp[$i];
}
}
//do some test:
$arr = array(4, 7, 6, 3, 9, 5, 8);
mergeSort($arr);
print_r($arr);
参考资料:http://blog.phpha.com/archives/1683.html
四、堆排序
主要思想:
堆积排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
(堆可以视为一棵完全的二叉树,完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示,每一个结点对应数组中的一个元素 )
节点与数组索引关系
对于给定的某个结点的下标i,可以很容易的计算出这个结点的父结点、孩子结点的下标,而且计算公式很漂亮很简约
代码实现:
/**
* 使用异或交换2个值,原理:一个值经过同一个值的2次异或后,原值不变
* @param int $a
* @param int $b
*/
function swap(&$a,&$b){
$a = $a^$b;
$b = $a^$b;
$a = $a^$b;
}
/**
* 整理当前树节点($n),临界点$last之后为已排序好的元素
* @param int $n
* @param int $last
* @param array $arr
*
*/
function adjustNode($n,$last,&$arr){
$l = $n<<1; // 左孩子
if( !isset($arr[$l])||$l>$last ){
return ;
}
$r = $l+1; // 右孩子
// 如果右孩子比左孩子大,则让父节点与右孩子比
if( $r<=$last&&$arr[$r]>$arr[$l] ){
$l = $r;
}
// 如果其中子节点$l比父节点$n大,则与父节点$n交换
if( $arr[$l]>$arr[$n] ){
swap($arr[$l],$arr[$n]);
// 交换之后,父节点($n)的值可能还小于原子节点($l)的子节点的值,所以还需对原子节点($l)的子节点进行调整,用递归实现
adjustNode($l, $last, $arr);
}
}
/**
* 堆排序(最大堆)
* @param array $arr
*/
function heapSort(&$arr){
// 最后一个算数位
$last = count($arr);
// 堆排序中常忽略$arr[0]
array_unshift($arr, 0);
// 最后一个非叶子节点
$i = $last>>1;
// 整理成最大堆,最大的数放到最顶,并将最大数和堆尾交换,并在之后的计算中,忽略数组最后端的最大数(last),直到堆顶(last=堆顶)
while(true){
adjustNode($i, $last, $arr);
if( $i>1 ){
// 移动节点指针,遍历所有节点
$i--;
}
else{
// 临界点$last=1,即所有排序完成
if( $last==1 ){
break;
}
swap($arr[$last],$arr[1]);
$last--;
}
}
// 弹出第一个元素
array_shift($arr);
}
参考资料:http://www.cnblogs.com/iampeter/p/3223487.html
五、选择排序
主要思想:
1. 首先在未排序序列中找到最小元素,存放到排序序列的起始位置
2. 然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾
3. 以此类推,直到所有元素均排序完毕
代码实现:
function selectSort( Array $arr){
$len = count($arr);
for( $i = 0; $i < $len ; $i ++){
for($j = $i; $j < $len ; $j ++){
if( $arr[$i] > $arr[$j]){
$temp = $arr[$i];
$arr[$i] = $arr[$j];
$arr[$j] = $temp;
}
}
}
return $arr;
}
$arr = array(23,1,45,12,7,19);
var_dump(selectSort($arr));
六、冒泡排序
主要思想:
1. 比较相邻的元素。如果第一个比第二个大,就交换他们两个
2. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对;这样,最后的元素应该会是最大的数
3. 以此类推,针对所有的元素重复以上的步骤,除了最后一个。
代码实现:
function bubbleSort( Array $arr){
$len = count($arr);
for($i = 0; $i < $len - 1; $i ++){
for($j = 0; $j < $len - 1 - $i ; $j ++){
if( $arr[$j] > $arr[$j+1]){
$temp = $arr[$j];
$arr[$j] = $arr[$j+1];
$arr[$j+1] = $temp;
}
}
}
return $arr;
}
$arr = array(23,1,45,12,7,19);
var_dump(bubbleSort($arr));
七、插入排序
主要思想:
1. 从第一个元素开始,该元素可以认为已经被排序
2. 取出下一个元素,在已经排序的元素序列中从后向前扫描
3. 如果该元素(已排序)大于新元素,将该元素移到下一位置
4. 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到该位置中
6. 重复步骤2
代码实现:
function insertSort(&$arr){
$len = count($arr);
// 默认下标为0的是已排好序的
for($i = 1; $i < $len ; $i ++){
$insertValue = $arr[$i]; // 待插入数据
$insertIndex = $i - 1;
while($insertIndex >= 0 && $insertValue < $arr[$insertIndex]){
// 数组后移
$arr[$insertIndex + 1] = $arr[$insertIndex];
$insertIndex -- ;
}
$arr[$insertIndex + 1] = $insertValue;
}
}
$arr = array(23,1,45,12,7,19);
insertSort($arr);
var_dump($arr);
八、希尔排序
主要思想:
希尔排序,也称递减增量排序算法,是插入排序的一种高速而稳定的改进版本。
希尔排序的大体思路是:将一个未排序的序列分成多个组,然后在组内使用插入排序对组内序列排序。我们的分组方式是将每隔固定位置(增量)的元素分成一组。之后去调整这个间隔大小,重新分组,组内重新排序。直到分组的间隔为1,也就是所有的元素分成一组,再进行一次插入排序,这样就可以完成整个序列的排序过程。
分组序列称之为希尔排序的增量序列,增量序列有一个非常流行的选择称之为希尔增量(希尔这个人建议的增量序列):假设序列为ht...hk hk-1 .. h1 ,排序序列的长度为N,那么ht = N除以2的商, 而hk-1 = hk 除以2的商,直到h1 = 1;
例如如果待排序数组的长度为 10,那么序列为 5, 2, 1;
代码实现:
function shellSort(&$arr) {
$len = count($arr);
//确定增量序列
//php内没有整除 采用floor向下去整
for($inc=floor($len/2); $inc>=1; $inc=floor($inc/2)) {
//内部实现与插入排序类似
//不过比较的元素取决于增量
for($i=$inc; $i<$len; ++$i) {
$tmp = $arr[$i];
for($j=$i-$inc; $j>=0 && $tmp<$arr[$j]; $j-=$inc) {
$arr[$j+$inc] = $arr[$j];
}
$arr[$j+$inc] = $tmp;
}
}
}
$arr = array(23,1,45,12,7,19);
shellSort($arr);
var_dump($arr);
参考资料:http://bbs.itcast.cn/thread-7315-1-1.html

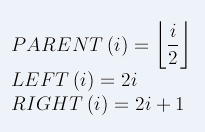

 浙公网安备 33010602011771号
浙公网安备 33010602011771号