卷积
卷积概述
第一节 领域
统计学中,加权的滑动平均是一种卷积。
概率论中,两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。
声学中,回声可以用源声与一个反映各种反射效应的函数的卷积表示。
电子工程与信号处理中,任一个线性系统的输出都可以通过将输入信号与系统函数(系统的冲激响应)做卷积获得。
物理学中,任何一个线性系统(符合叠加原理)都存在卷积。
计算机科学中,卷积神经网络(CNN)是深度学习算法中的一种,近年来被广泛用到模式识别、图像处理等领域中。
第二节 定义
(1)通俗理解:
某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的输出,然后再把不同时刻的输出点放在一起,形成一个函数,这就是卷积,卷积之后的函数就是你脸上的包的大小随时间变化的函数。
(2)数学理解:
一维卷积:
连续:
离散:
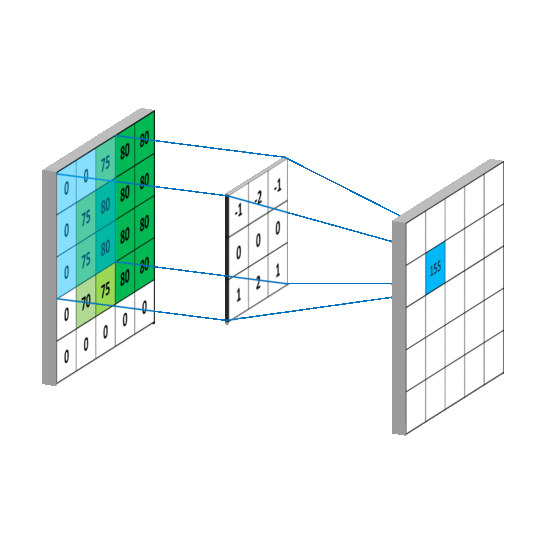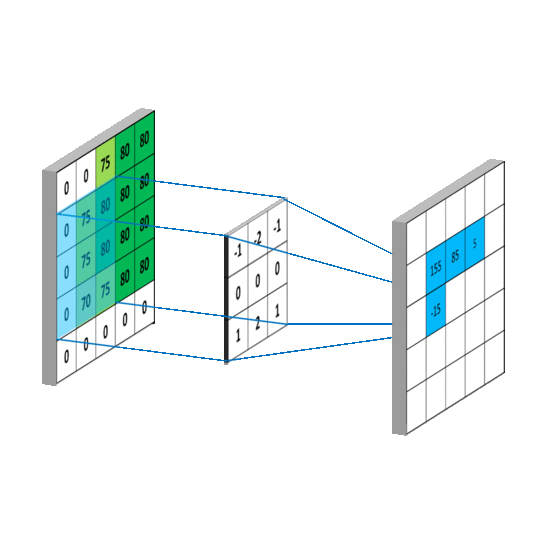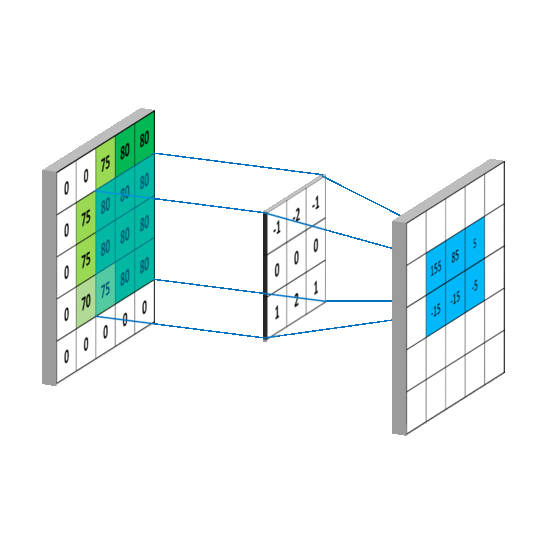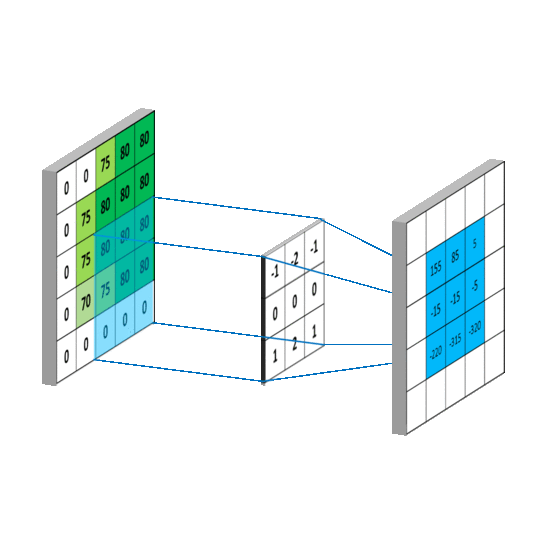
二维卷积:
连续:
离散:
(3)泛函定义
通过两个函数f和g生成第三个函数的一种数学算子,表征函数f与经过翻转和平移的g的乘积函数所围成的曲边梯形的面积。如果将参加卷积的一个函数看作区间的指示函数,卷积还可以被看作是“移动平均”的推广。
第三节 计算
(1)直接计算
(2)FFT
由于两个离散信号在时域(time domain)做卷积相当于这两个信号的离散傅里叶变换在频域(frequency domain)做相乘。
;
;
;
;
第四节 性质
卷积定理:函数卷积的傅里叶变换是函数傅里叶变换的乘积。即,一个域中的卷积相当于另一个域中的乘积,例如时域中的卷积就对应于频域中的乘积。
参考文献
离散卷积的理解:https://blog.csdn.net/bitcarmanlee/article/details/54729807
对卷积的通俗理解:http://mengqi92.github.io/2015/10/06/convolution/
关于卷积效果的演示动画:https://graphics.stanford.edu/courses/cs178/applets/convolution.html
卷积神经网络的经典论文:
[1] LeCun, B.Boser, J.S.Denker, D.Henderson, R.E.Howard, W.Hubbard, and L.D.Jackel. Backpropagation applied to handwritten zip code recognition. Neural Computation, 1989.
[2] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel. Handwritten digit recognition with a back-propagation network. In David Touretzky, editor, Advances in Neural Information Processing Systems 2 (NIPS*89), Denver, CO, Morgan Kaufman, 1990.
[3] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, november 1998.
[4] Alex Krizhevsky, Ilya Sutskever, Geoffrey E.Hinton. ImageNet Classification with Deep Convolutional Neural Networks. 2012.
[5] Zeiler M D, Fergus R. Visualizing and Understanding Convolutional Networks. European Conference on Computer Vision, 2013.
[6] Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, Andrew Rabinovich, Going Deeper with Convolutions, Arxiv Link:arxiv.org/abs/1409.4842.
[7] K. Simonyan and A. Zisserman. Very Deep Convolutional Networks for Large-Scale Image Recognition. international conference on learning representations. 2015.
[8] Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. Deep Residual Learning for Image Recognition. computer vision and pattern recognition, 2015.
[9] Andreas Veit,Michael J Wilber, Serge J Belongie. Residual Networks Behave Like Ensembles of Relatively Shallow Networks. neural information processing systems, 2016.
[10] Long J, Shelhamer E, Darrell T, et al. Fully convolutional networks for semantic segmentation. Computer Vision and Pattern Recognition, 2015.
卷积神经网络之父:Yann LeCun


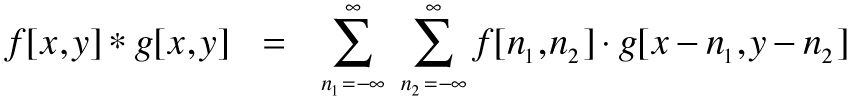
![y[n]=f[n]*g[n]=\sum _{m=0}^{M-1}f[n-m]g[m]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1081139aae46ebd7421e11ec20351dc12688cedd)
![y[n]=f[n]*g[n]\leftrightarrow Y[f]=F[f]G[f]](https://wikimedia.org/api/rest_v1/media/math/render/svg/27f83ca717dff1b21da43e56127c50874843b8b0) ;
;![F[f]=DFT_{P}(f[n]),G[f]=DFT_{P}(g[n])](https://wikimedia.org/api/rest_v1/media/math/render/svg/af332366ed1070784c006329adcd40833e64c44d) ;
;![Y[f]=DFT_{P}(f[n])DFT_{P}(g[n])](https://wikimedia.org/api/rest_v1/media/math/render/svg/93ec9e3130dcd720d4d6b1930bd492f29fee0faf) ;
;![y[n]=IDFT_{P}{DFT_{P}(f[n])DFT_{P}(g[n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc12d1e8c9712ca85bf040d7e8573842c545588) ;
;








 浙公网安备 33010602011771号
浙公网安备 33010602011771号