机器学习【六】支持向量机SVM——专治线性不可分
SVM原理
线性可分与线性不可分
线性可分
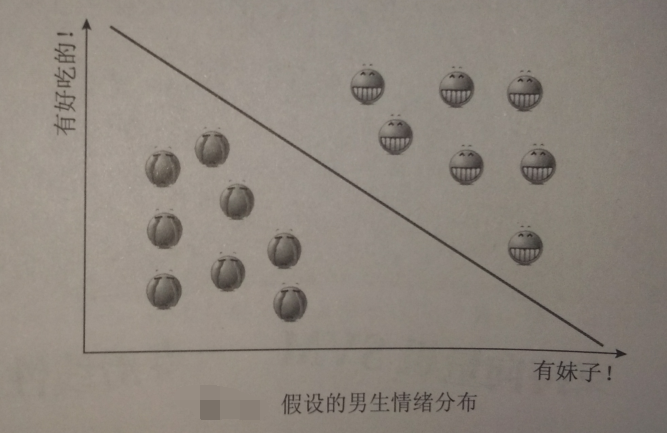
线性不可分-------【无论用哪条直线都无法将女生情绪正确分类】
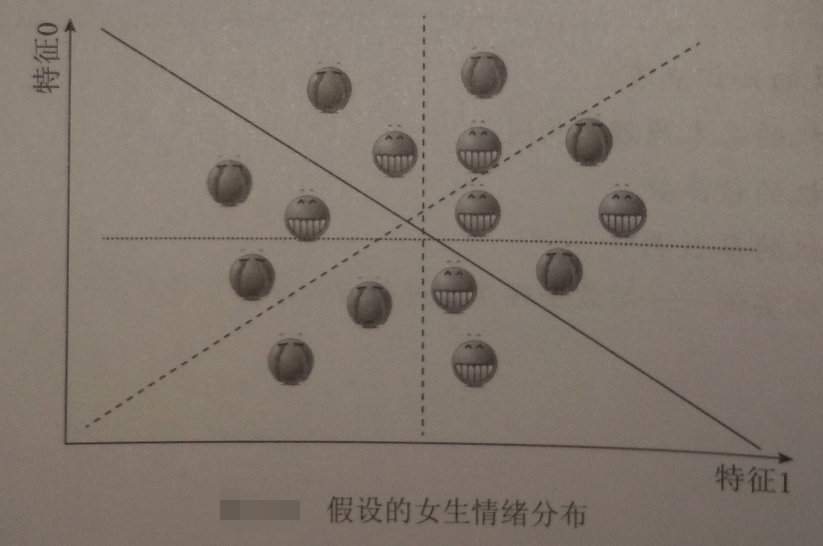
SVM的核函数可以帮助我们:
假设‘开心’是轻飘飘的,“不开心”是沉重的
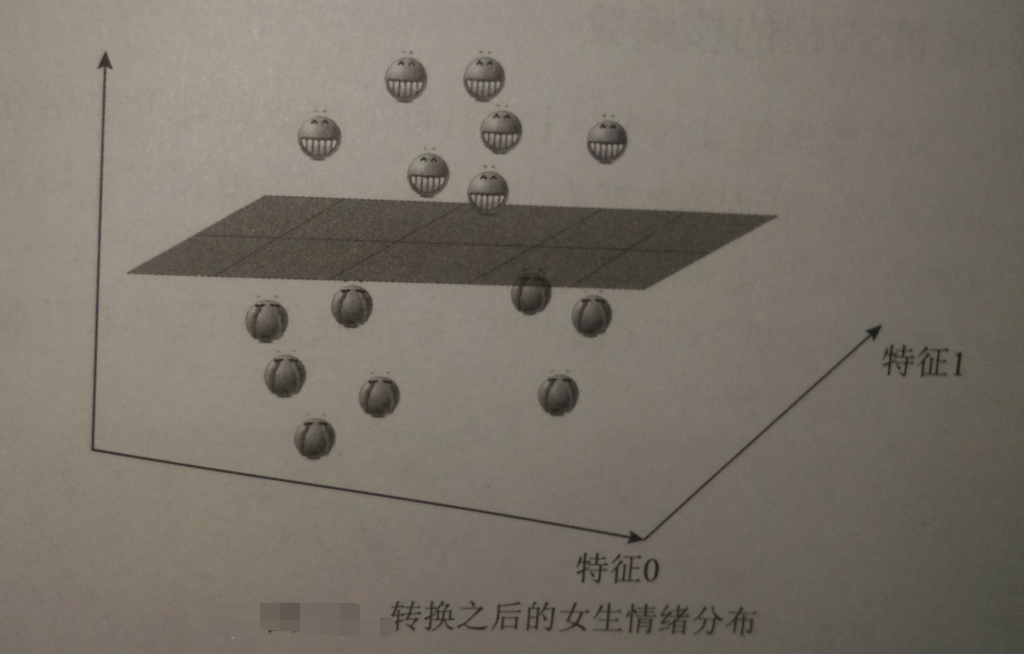
将三维视图还原成二维:
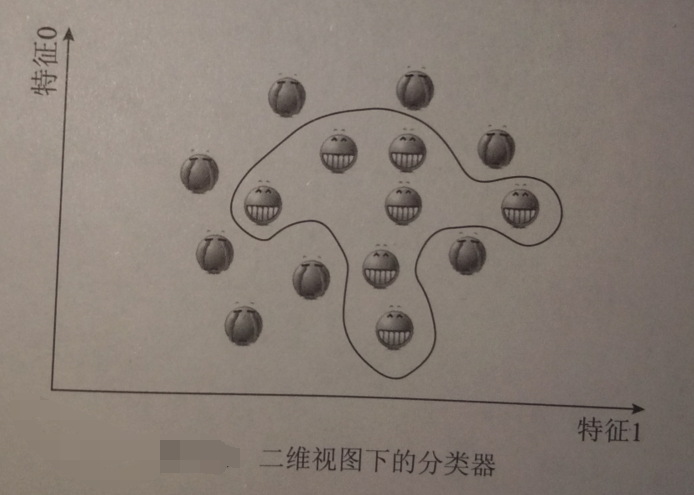
刚利用“开心”“不开心”的重量差实现将二维数据变成三维的过程,称为将数据投射至高维空间,这正是核函数的功能
在SVM中,用的最普遍的两种把数据投射到高维空间的方法分别是多项式内核、径向基内核(RFB)
多项式内核:
通过把样本原始特征进行乘方来把数据投射到高维空间【如特征1^2,特征2^3,特征3^5......】
RBF:
又称高斯内核
支持向量机的SVM核函数

用图形直观了解:
#导入numpy
import numpy as np
#导入画图工具
import matplotlib.pyplot as plt
#导入支持向量机SVM
from sklearn import svm
#导入数据集生成工具
from sklearn.datasets import make_blobs
#先创建50个数据点,让它们分成两类
X,y = make_blobs(n_samples=50,centers=2,random_state = 6)
#创建一个线性内核的支持向量机模型
clf = svm.SVC(kernel = 'linear',C=1000)
clf.fit(X,y)
#把数据点画出来
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
#建立图像坐标
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#生成两个等差数列
xx = np.linspace(xlim[0],xlim[1],30)
yy = np.linspace(ylim[0],ylim[1],30)
YY,XX = np.meshgrid(yy,xx)
xy = np.vstack([XX.ravel(),YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
#把分类的边界画出来
ax.contour(XX,YY,Z,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])
ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=100,linewidth=1,facecolors='none')
plt.show()
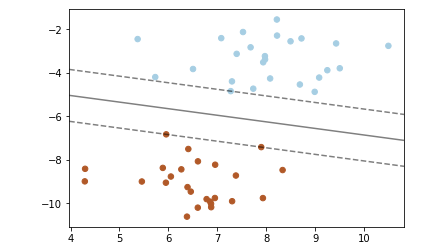 ——线性内核的SVM分类器
——线性内核的SVM分类器
【结果分析】:
在分类器两侧有两条虚线,正好压在虚线上的数据点,即支持向量
本例所使用的方法称为“最大边界间隔超平面”
指,实线【在高维数据中是一个超平面】和所有支持向量的距离都是最大的
把SVM的内核换成RBF:
#创建一个RBF内核的支持向量机模型
clf_rbf = svm.SVC(kernel='rbf',C=1000)
clf_rbf.fit(X,y)
#把数据点画出来
plt.scatter(X[:,0],X[:,1],c=y,s=30,cmap=plt.cm.Paired)
#建立图像坐标
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#生成两个等差数列
xx = np.linspace(xlim[0],xlim[1],30)
yy = np.linspace(ylim[0],ylim[1],30)
YY,XX = np.meshgrid(yy,xx)
xy = np.vstack([XX.ravel(),YY.ravel()]).T
Z = clf_rbf.decision_function(xy).reshape(XX.shape)
#把分类的边界画出来
ax.contour(XX,YY,Z,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])
ax.scatter(clf_rbf.support_vectors_[:,0],clf_rbf.support_vectors_[:,1],s=100,linewidth=1,facecolors='none')
plt.show()
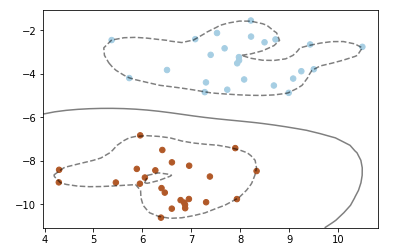 ——RBF内核的SVM分类器
——RBF内核的SVM分类器
【结果分析】:
使用RBF内核时,数据点距离计算是用如下公式计算的:
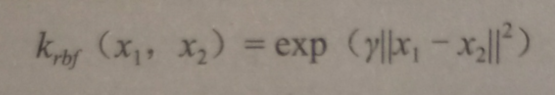

SVM的核函数和参数选择
1.不同核函数的SVM对比
线性模型中提到过,linearSVM算法,就是一种使用了线性内核的SVM算法,不过linearSVM不支持对核函数进行修改【默认只能使用线性内核】
直观体验不同内核的SVM算法在分类中的不同表现:
from sklearn.datasets import load_wine
#定义一个函数来画图
def make_meshgrid(x,y,h=.02):
x_min,x_max = x.min() -1,x.max() +1
y_min,y_max = y.min() -1,y.max() +1
xx,yy = np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
return xx,yy
#定义一个绘制等高线的函数
def plot_contours(ax,clf,xx,yy, **params):
Z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx,yy,Z, **params)
return out
#使用酒的数据集
wine = load_wine()
#选取数据集的前两个特征
X = wine.data[:,:2]
y = wine.target
C = 1.0 #SVM的正则化参数
models = (clf.fit(X,y) for clf in models)
#设定图题
titles = ('SVC with linear kernal','LinearSVC (linear kernal)','SVC with RBF kernal','SVC with polynomial (degree 3) kernal')
#设定一个子图形的个数和排列方式
fig,sub = plt.subplots(2,2)
plt.subplots_adjust(wspace=0.4,hspace=0.4)
#使用前面定义的函数进行画图
X0,X1 = X[:,0],X[:,1]
xx,yy = make_meshgrid(X0,X1)
plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolors='k')
ax.set_xlim(xx.min(),xx.max())
ax.set_ylim(yy.min(),yy.max())
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
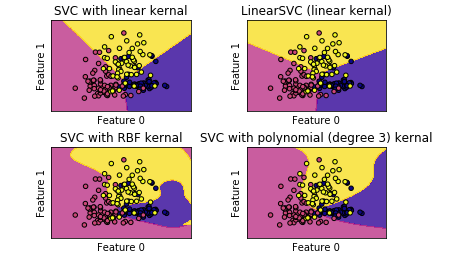
【结果分析】:
线性内核的SVC与linearSVC得到的结果近似,但仍然有一点差别——原因是linearSVC对L2范数进行最小化,而线性内核的SVC是对L1进行最小化
无论如何,线性内核的SVC和linearSVC生成的决定边界都是线性的【在更高维数据集中将会是相交的超平面】
RBF内核的SVC和polynomial内核的SVC分类器的决定边界则完全不是线性的,更加弹性
决定他们边界形状的是参数:
polynomial内核的SVC分类器
degree和正则化参数C
【本例中degree=3,即对原始数据集的特征乘3次方操作】
RBF内核的SVC
gamma和正则化参数C
RBF内核SVC的gamma参数调节
models = (clf.fit(X,y) for clf in models)
#设定图题
titles = ('gamma=0.1','gamma=1','gamma=10')
#设置子图形个数和排列
flg,sub = plt.subplots(1,3,figsize=(10,3))
X0,X1 = X[:,0],X[:,1]
xx,yy = make_meshgrid(X0,X1)
plot_contours(ax,clf,xx,yy,cmap=plt.cm.plasma,alpha=0.8)
ax.scatter(X0,X1,c=y,cmap=plt.cm.plasma,s=20,edgecolors='k')
ax.set_xlim(xx.min(),xx.max())
ax.set_ylim(yy.min(),yy.max())
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
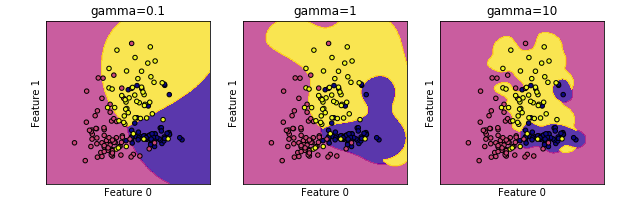
【结果分析】:
gamma值越小,RBF内核的直径越大——> 有更多的点被模型圈进决定边界中——> 边界越圆滑
- gamma越小,模型倾向于 欠拟合
- gamma越大,模型倾向于 过拟合
正则化参数C,可以见线性模型一章
- C越小,模型越受限【单个数据对模型的影响越小】,模型越简单
- C越大,每个数据点对模型的影响越大,模型越复杂
SVM优点
- 可应对高维数据集和低维数据集
- 即使数据集中样本特征的测度都比较接近,如图像识别领域,以及样本特征数和样本数比较接近的时候,都游刃有余
SVM缺点
- 当数据集中特征数量在1万以内,SVM可以驾驭,但数量大于10万,就非常占内存和耗费时间
- 对数据预处理和参数调节要求很高
【注意】
SVM中3个参数非常重要:
- 核函数的选择
- 核函数的参数【如RBF的gamma】
- 正则化参数C
RBF内核的gamma值是用来调节内核宽度的,gamma值和C值一起控制模型的复杂度,数值越大,模型越复杂【实际中,一起调节,才能达到最好的效果】
实战
SVM在回归分析中的应用——波士顿房价数据集
1.了解数据集
#导入波士顿房价
from sklearn.datasets import load_boston
boston = load_boston()
#打印键
print(boston.keys())
#打印数据集中的短描述
print(boston['DESCR'])

【一部分】
【结果分析】
数据集共有506个样本,每个样本有13个特征变量,后面还有一个叫做中位数的第14个变量【这变量就是该数据集中的target】
2.通过SVR算法建立房价预测模型
#导入数据集拆分工具
from sklearn.model_selection import train_test_split
#建立数据集和测试集
X,y = boston.data,boston.target
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=8)
#打印训练集和测试集的形态
print(X_train.shape)
print(X_test.shape)

用SVR建模
#导入支持向量回归模型
from sklearn.svm import SVR
#分别测试linear核函数和rbf核函数
for kernel in ['linear','rbf']:
svr = SVR(kernel=kernel)
svr.fit(X_train,y_train)
print(kernel,'核函数模型训练集得分:',svr.score(X_train,y_train))
print(kernel,'核函数模型测试集得分:',svr.score(X_test,y_test))

SVM算法对数据预处理的要求较大,如果 数据特征量级差异较大 ,就需要预处理数据
先用图形可视化:
#将特征数值中的min和max用散点图画出来
plt.plot(X.min(axis=0),'v',label='min')
plt.plot(X.max(axis=0),'^',label='max')
#设定纵坐标为对数形式
plt.yscale('log')
#设定图注位置最佳
plt.legend(loc='best')
plt.xlabel('features')
plt.ylabel('feature magnitude')
plt.show()
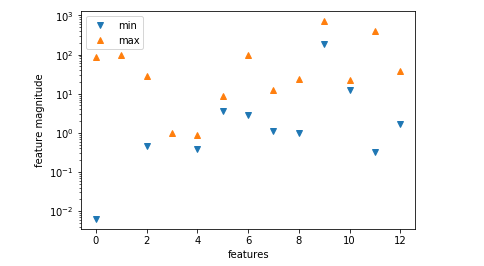
显然,量级差异较大
预处理:
from sklearn.preprocessing import StandardScaler
#预处理
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
#将预处理后的数据特征的max和min用散点图表示出来
plt.plot(X_train_scaled.min(axis=0),'v',label='train set min')
plt.plot(X_train_scaled.max(axis=0),'^',label='train set max')
plt.plot(X_test_scaled.min(axis=0),'v',label='test set min')
plt.plot(X_test_scaled.max(axis=0),'^',label='test set max')
plt.legend(loc='best')
plt.xlabel('scaled features')
plt.ylabel('scaled feature magnitude')
plt.show()
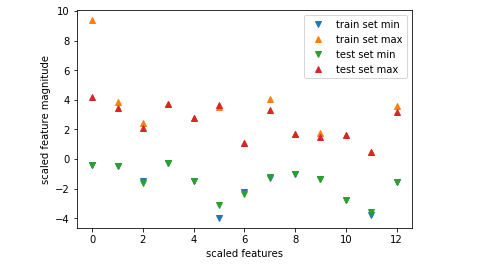
【结果分析】
经过预处理,无论训练集还是测试集,所有特征的最大值不会超过10,最小值趋近0,以至图中看不到
用预处理的数据训练模型:
#使用预处理后的数据重新训练模型
for kernel in ['linear','rbf']:
svr = SVR(kernel=kernel)
svr.fit(X_train_scaled,y_train)
print(kernel,'训练集得分:',svr.score(X_train_scaled,y_train))
print(kernel,'测试集得分:',svr.score(X_test_scaled,y_test))

进一步调整参数
#设置模型的C参数和gamma参数
svr = SVR(C=100,gamma=0.1)
svr.fit(X_train_scaled,y_train)
print('训练集得分:',svr.score(X_train_scaled,y_train))
print('测试集得分:',svr.score(X_test_scaled,y_test))
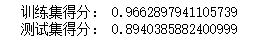




 浙公网安备 33010602011771号
浙公网安备 33010602011771号