机器学习【二】广义线性模型
广义线性模型 —— 一类预测模型【不是一个】
使用输入数据集的特征的线性函数进行建模,并对结果进行预测的方法
线性模型的训练非常快
过程也很容易被人理解
但,当数据集的特征比较少的时候,线性模型的表现就会相对偏弱
一般公式

也就是,模型给出的预测可以看作是输入特征的加权和,而w就代表了每个特征的权值【可以是负数】
 读作“ y hat ” ,代表y的估计值
读作“ y hat ” ,代表y的估计值
用Jupyter Notebook 画出直线 y=0.5x+3
import numpy as np
import matplotlib.pyplot as plt
#令x为-5,5之间,元素数为100的等差数列
x = np.linspace(-5,5,100)
#输入直线方程
y = 0.5*x+3
plt.plot(x,y,c='orange')
plt.title('Straight Line')
plt.show()

如上,线性模型正是通过训练数据集确定自身的系数【斜率】和截距的
线性模型的图形表示
1.由(1,3),(4,5)两点画直线
#导入线性回归模型
from sklearn.linear_model import LinearRegression
#输入二点横坐标
X = [[1],[4]]
#输入二点纵坐标
y = [3,5]
#用线性模型拟合这两个点
lr = LinearRegression().fit(X,y)
#画出两个点和直线的图形
z = np.linspace(0,5,20)
plt.scatter(X,y,s=80)
plt.plot(z, lr.predict(z.reshape(-1,1)),c='k')
plt.title('Straight Line')
plt.show()
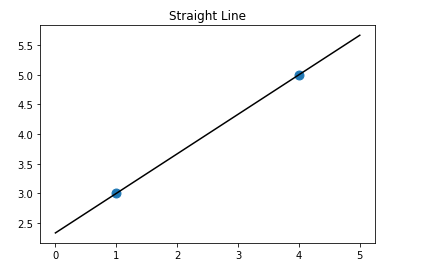
确定该直线方程:
print('斜率:',lr.coef_[0])
print('截距:',lr.intercept_)
斜率: 0.6666666666666664
截距: 2.333333333333334
2.新加(3,3)点,画直线:
#导入线性回归模型
from sklearn.linear_model import LinearRegression
#输入二点横坐标
X = [[1],[4],[3]]
#输入二点纵坐标
y = [3,5,3]
#用线性模型拟合这三个点
lr = LinearRegression().fit(X,y)
#画出两个点和直线的图形
z = np.linspace(0,5,20)
plt.scatter(X,y,s=80)
plt.plot(z, lr.predict(z.reshape(-1,1)),c='k')
plt.title('Straight Line')
plt.show()
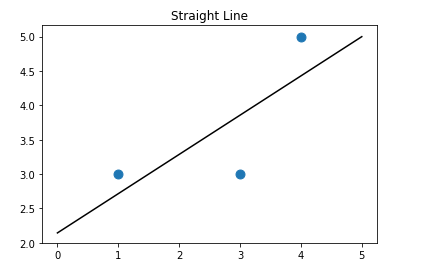
print('斜率:',lr.coef_[0])
print('截距:',lr.intercept_)
斜率: 0.5714285714285713 截距: 2.1428571428571432
线性回归模型的原理:
让自己距离 每个数据点的 加和为最小值
3.利用sklearn生成的make_regression数据集为例:
from sklearn.datasets import make_regression
#生成用于回归分析的数据集
X,y = make_regression(n_samples=50,n_features=1,n_informative=1,noise=50,random_state=1)
#使用线性模型对数据进行拟合
reg = LinearRegression()
reg.fit(X,y)
#z是我们生成的等差数列,用来画出线性模型的图形
z = np.linspace(-3,3,200).reshape(-1,1)
plt.scatter(X,y,c='b',s=60)
plt.plot(z,reg.predict(z),c='k')
plt.title('Linear Regression')
plt.show()
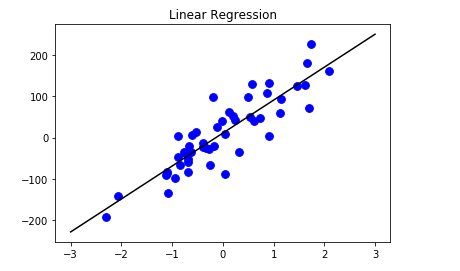
print('斜率:',reg.coef_[0])
print('截距:',reg.intercept_)
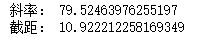
如上,该直线距离50个数据点的距离之和是最小的
可能注意到 coef_ 和 intercept_ 这两个属性以 '_' 结尾
这是sklearn的一个特点,总是用下划线作为来自训练数据集的属性的结尾
以便将它们与由用户设置的参数区分开
线性模型特点
以上使用的都是特征数只有1个的数据集
用于回归分析的线性模型在特征数为1的数据集章,使用一条直线作预测分析
特征数为2时,是一个平面
更多——> 高纬度的超平面
线性模型的预测方法局限——> 很多数据没有体现到这条直线上,因为使用线性模型的前提条件,是假设目标y是数据特征的线性组合
对于特征变量较多的数据集,线性模型会十分强大【尤其是训练集的特征变量 > 数据点的数量时,可以达到近乎完美的预测】
用于回归分析的线性模型有好几类,区别:
如何从训练集中确定参数w,b,如何控制模型的复杂度
最基本的线性模型——线性回归
线性回归,也称普通最小二乘法OLS
1.线性回归的基本原理:
找到当训练集中y的预测值和其真实值平方差最小的时候所对应的w值 b值
线性回归没有可供用户调节的参数【优势,但也意味着无法控制模型的复杂性】
#使用make_regression函数,生成一个样本数量为100,特征数量为2的数据集,并利用 train_test_split 函数将数据集分割成训练集和测试集,再用线性回归模型计算出w、b值
#导入数据集拆分工具
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X,y = make_regression(n_samples=100,n_features=2,n_informative=2,random_state=38)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=8)
lr = LinearRegression().fit(X_train,y_train)
print('斜率w:',lr.coef_[:])
print('截距b:',lr.intercept_)
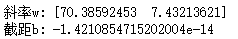
intercept_ 属性一直是是一个浮点数,而coef_ 属性则是一个Numpy的数组【其中每个特征对应数据中的一个数值】
#由于使用的make_regression 生成的数据集中数据点有2个特征,所以lr.coef_ 是一个二维数组
所以,本例中,线性回归方程可以表示为:
y = 73.3859 * X1 + 7.4321 * X2 - 1.42e-14
2.线性回归的性能表现
print(lr.score(X_train,y_train))
print(lr.score(X_test,y_test))
1.0 1.0
没有向数据集中加入noise,自然满分
3.真实的数据集:【特征多,noise多】
from sklearn.datasets import load_diabetes
#载入糖尿病数据集
X,y = load_diabetes().data, load_diabetes().target
#将数据集拆分为训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=8)
#使用线性模型拟合
lr = LinearRegression().fit(X_train,y_train)
#得分
print(lr.score(X_train,y_train))
print(lr.score(X_test,y_test))
0.5303814759709331 0.45934404966916426
#在训练集和测试集上得分的巨大差异——> 出现过拟合问题,所以应该找到一个模型,是我们能够控制模型的复杂度——> 岭回归
使用L2正则化的线性模型——岭回归
【实际上,是一种改良的最小二乘法】
【一种能够避免过拟合的线性模型】
1.原理

#岭回归在sklearn中通过linear_model.Ridge 函数来调用
#导入岭回归
from sklearn.linear_model import Ridge
#使用岭回归对数据拟合
rd = Ridge().fit(X_train,y_train)
#得分
print(rd.score(X_train,y_train))
print(rd.score(X_test,y_test))
0.4326376676137663 0.43252177690681864
#复杂度越低的模型。在训练集上表现的越差,但是其泛化的能力更好,如果我们在意的是模型在泛化上的表现,就应该选择岭回归
2.参数调节
【岭回归是在模型的简单性(使系数趋近于0)和它在训练集上的性能之间取得平衡的一种模型】
可以使用alpha参数控制模型的更加简单性还是性能更好
【上方例子使用默认参数alpha = 1】

#导入岭回归
from sklearn.linear_model import Ridge
#使用岭回归对数据拟合,修改alpha参数为10
rd10 = Ridge(alpha=10).fit(X_train,y_train)
#得分
print(rd10.score(X_train,y_train))
print(rd10.score(X_test,y_test))
0.15119962367011153 0.16202013428866247
#测试得分>训练得分,说明如果我们的模型出现了过拟合现象,可以提高alpha的值来降低过拟合的程度
如果降低 alpha 的值,会让系数的限制不严格,如果使用非常小的值,系统的限制可以忽略不计,结果会非常接近线性回归
#导入岭回归
from sklearn.linear_model import Ridge
#使用岭回归对数据拟合,修改alpha参数为0.1
rd1 = Ridge(alpha=0.1).fit(X_train,y_train)
#得分
print(rd1.score(X_train,y_train))
print(rd1.score(X_test,y_test))
0.5215646055241339 0.4734019500945309
【可以尝试降低alpha的值,改善模型的泛化表现 { 测试得分增大 } 】
为了清晰看出 alpha 值对模型的影响,可以观察 alpha 参数对应的模型的 coef_ 参数:
【较高的 alpha 代表模型的限制更严格,所以高 alpha 下,coef_数值更大】
#导入岭回归
from sklearn.linear_model import Ridge
#使用岭回归对数据拟合
rd = Ridge(alpha=1).fit(X_train,y_train)
rd10 = Ridge(alpha=10).fit(X_train,y_train)
rd0 = Ridge(alpha=0.1).fit(X_train,y_train)
#绘制alpha=1时的模型参数
plt.plot(rd.coef_, 's',label='Ridge alpha=1')
plt.plot(rd10.coef_, '^',label='Ridge alpha=10')
plt.plot(rd0.coef_, 'v',label='Ridge alpha=0.1')
#绘制线性回归的系数作对比
plt.plot(lr.coef_, 'o',label='linear regression')
plt.xlabel('coefficient index')
plt.ylabel('coefficient magitude')
plt.hlines(0,0,len(lr.coef_))
plt.legend()
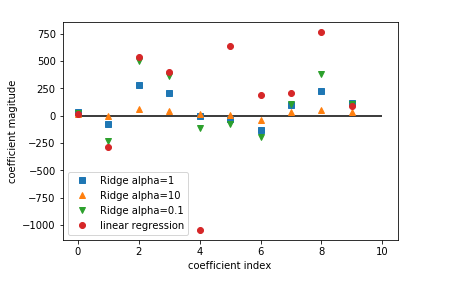
横轴代表的是 coef_ 属性:
X=0 显示第一个特征变量系数,X=1显示的是第二个特征变量的系数 。。。。。
当alpha=10时,特征变量系数大多0附近
当alpha=1时,岭模型的特征变量系数增大
alpha=0.1时,系数更大,甚至大部分与线性回归的点重合
而线性模型没经过任何正则处理,所以特征变量系数会非常大
另一个理解正则化对模型影响的方法——取一个固定的alpha,改变训练集的数据量
from sklearn.model_selection import learning_curve,KFold
#定制一个学习曲线的函数
def plot_learning_curve(est,X,y):
#将数据进行20次拆分用来对模型进行评分
training_set_size,train_scores,test_scores = learning_curve(est,X,y,train_sizes=np.linspace(.1,1,20),cv=KFold(20,shuffle=True,random_state=1))
estimator_name = est.__class__.__name__
line = plt.plot(training_set_size,train_scores.mean(axis=1),'--',label='training '+estimator_name)
plt.plot(training_set_size, train_scores.mean(axis=1),'-',label='test' + estimator_name,c=line[0].get_color())
plt.xlabel('Training set size')
plt.ylabel('Score')
plt.ylim(0,1.1)
plot_learning_curve(Ridge(alpha=1),X,y)
plot_learning_curve(LinearRegression(),X,y)
plt.legend(loc=(0,1.05),ncol=2,fontsize=11)
得下图,是一个随数据集大小而不断改变的模型评分折线图
其中的折线,称之为“学习曲线”
【书上的总共会出现4条曲线,但代码一样,原因未知,所以选取书上例图】
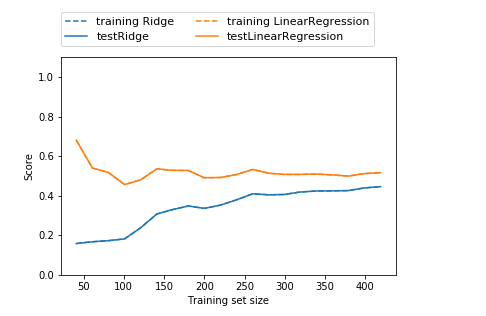
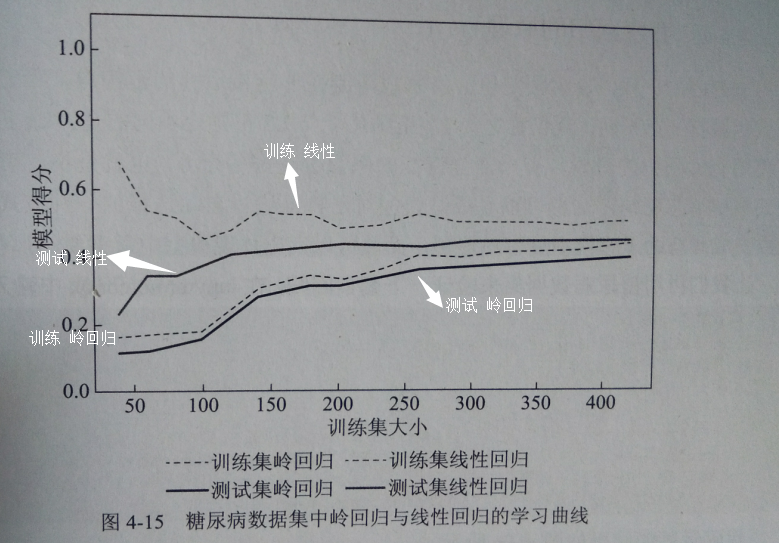
结论:
1.无论岭回归还是线性回归,训练集>测试集
2.岭回归是经过正则化的模型,所以,整个图像中,训练集要比线性回归的低
3.岭回归在 训练集 和 测试集 的得分差异低【尤其在数据子集比较小的情况】
4.数据量小于50,线性回归几乎让机器学不到任何东西
5.随着数据规模增大,线性回归的得分赶上了岭回归的得分——>【足够多的数据,正则化显得不重要,两模型表现差不多】
#随着数据量的增大,线性回归在训练集的得分下降——> 随着数据增加,线性模型越不容易产生过拟合现象 【即越难记住数据】
使用L1正则化的线性模型——套索回归
1.原理
同岭回归,也会将系数限制在非常接近0的范围内,但方法不同:有一部分特征的系数正好等于0
即,一部分特征会被模型忽略掉
from sklearn.linear_model import Lasso
#使用套索回归拟合数据
lasso = Lasso().fit(X_train,y_train)
#得分
print(lasso.score(X_train,y_train))
print(lasso.score(X_test,y_test))
print(np.sum(lasso.coef_ != 0)) #使用的特征数
0.36242428249291325 0.36561858962128
3
结果显示出模型发生了欠拟合的问题,在10个特征里套索回归之用了3个
与岭回归类似。套索回归也有一个正则化参数 alpha,用来控制 特征变量系数被约束到0的强度
2.参数调节
降低alpha的值 ——> 降低欠拟合的程度【同时还需要增大最大迭代次数】
#增大模型迭代次数的默认设置
#否则模型会提示我们增加最大迭代次数
lasso01 = Lasso(alpha=0.1,max_iter=100000).fit(X_train,y_train)
#得分 & 特征数
print(lasso01.score(X_train,y_train))
print(lasso01.score(X_test,y_test))
print(np.sum(lasso01.coef_ != 0))
0.519480608218357 0.47994757514558173 7
结果:
降低alpha 值可以拟合出更复杂的模型,从而在训练集和测试集都能获得良好表现
相对岭回归,套索回归表现稍好,且10个特征只用了7个,使模型更容易被理解
如果alpha 太低,等于把正则化的效果去除,可能出现过拟合
#把alpha 设置为0.0001
lasso000= Lasso(alpha=0.0001,max_iter=100000).fit(X_train,y_train)
#得分 & 特征数
print(lasso000.score(X_train,y_train))
print(lasso000.score(X_test,y_test))
print(np.sum(lasso000.coef_ != 0))
0.5303811330981303 0.4594509683706017 10
#使用全部的特征,而且测试集得分略低于alpha=0.1的情况——> 降低alpha 倾向让模型出现过拟合现象
套索回归和岭回归的区别
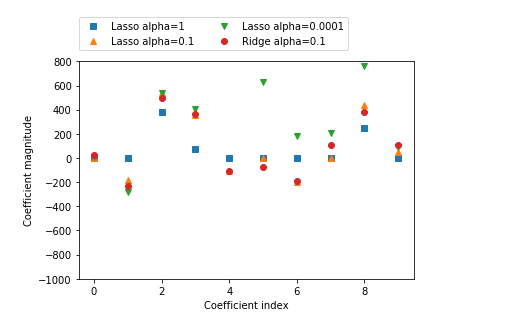
比较不同alpha 值的套索回归和岭回归进行系数对比:
#绘制alpha 值等于1时的模型系数
plt.plot(lasso.coef_ ,'s',label='Lasso alpha=1')
#绘制alpha 值等于0.1时的模型系数
plt.plot(lasso01.coef_, '^',label='Lasso alpha=0.1')
#绘制alpha 值等于0.001时的模型系数
plt.plot(lasso000.coef_, 'v',label='Lasso alpha=0.0001')
#绘制alpha=0.1 的岭回归模型系数作为对比
plt.plot(ridge01.coef_,'o',label='Ridge alpha=0.1')
plt.legend(ncol=2,loc=(0,1.05))
plt.ylim(-1000,800)
plt.xlabel('Coefficient index')
plt.ylabel('Coefficient magnitude')



 浙公网安备 33010602011771号
浙公网安备 33010602011771号