从几个典型例题来深入思考Backtracking

前言：
我自己的理解：backtracking是complete search+剪枝，最坏的复杂度是complete search,但是如果我们能发现不符合条件的 我们会提前剪枝，减少复杂度。
而且backtracking的最典型特征就是add-recursion-remove模式。

backtracking的本质实际上就是dfs
LC46 Permutation

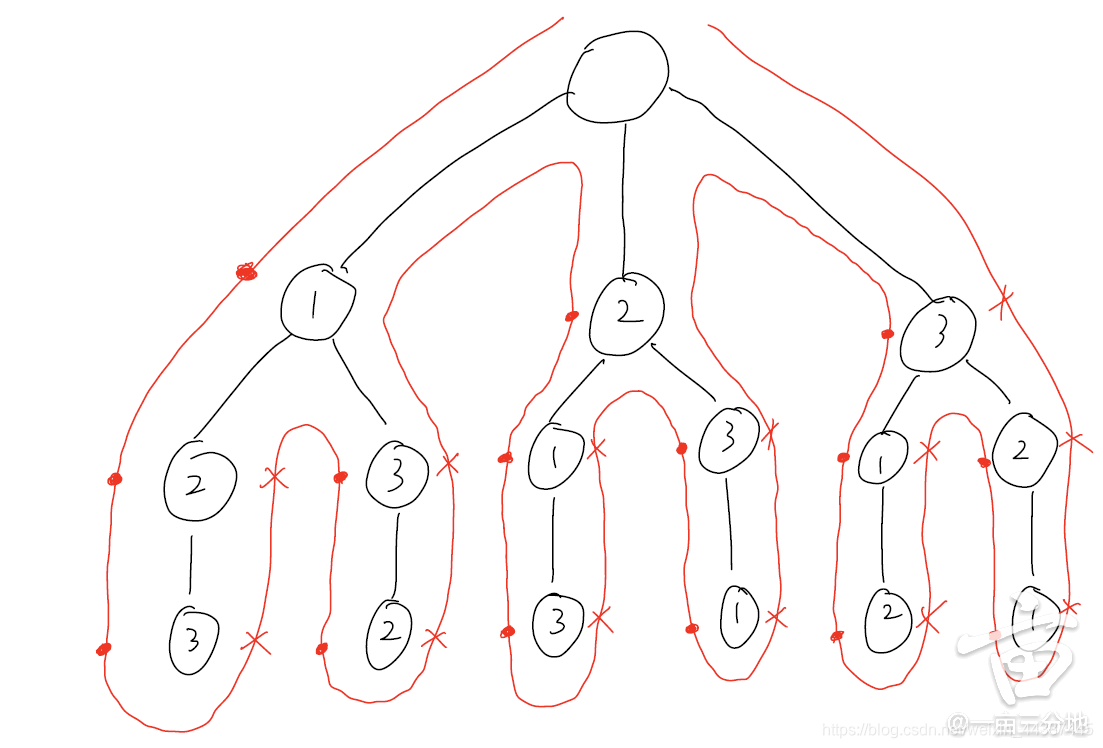
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> track = new ArrayList<>();
        backtrack(ans, track, nums);
        return ans;
    }
    private void backtrack(List<List<Integer>> ans, List<Integer> track, int[] nums) {
        if (track.size() == nums.length){
            ans.add(new ArrayList<>(track));
        }
        else {
            for (int i = 0;i < nums.length;++i){
                if (track.contains(nums)) {
  continue;
                }
                track.add(nums);
                backtrack(ans, track, nums);
                track.remove(track.size() - 1);
            }
        }
    }
}

LC78 Subsets
两种思路：
每一层都是add当前数值OR NOT

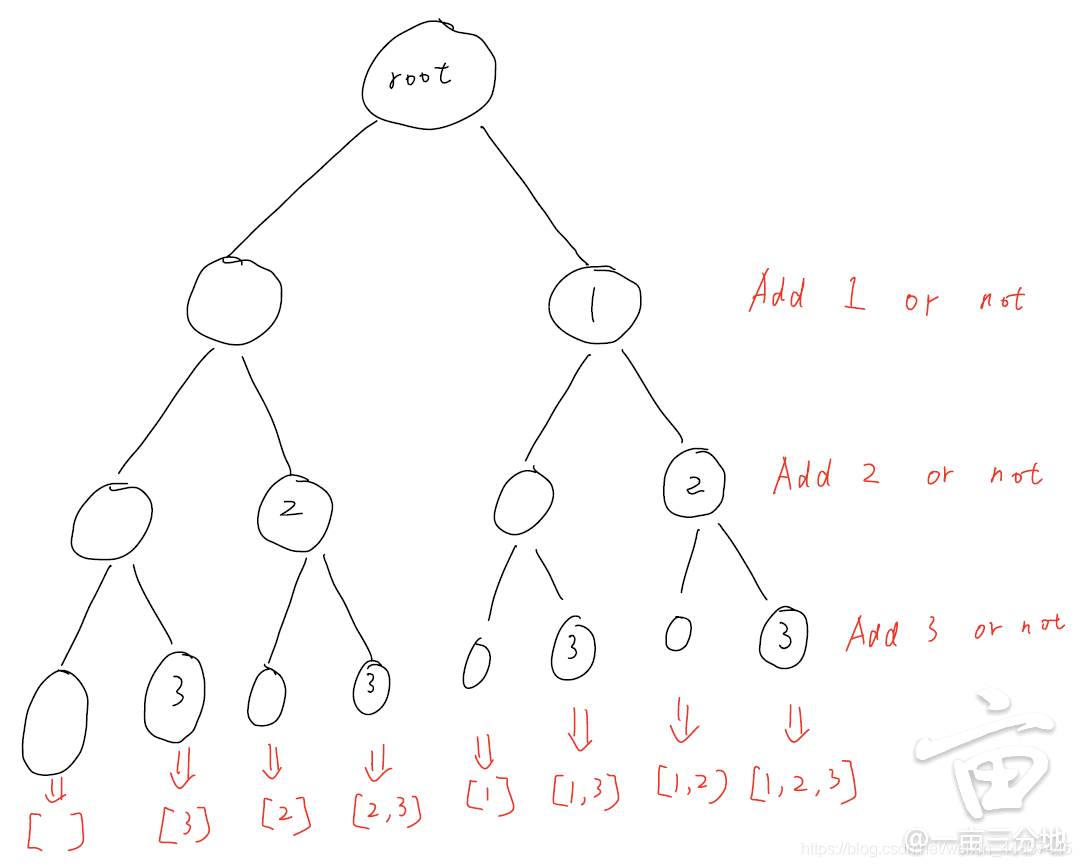
对应的代码：

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> track = new ArrayList<>();
        List<Integer> numslist = new ArrayList<>();
        for (int i: nums) numslist.add(i);
        backtrack(ans, track, numslist);
        return ans;
         
    }
     
    private void backtrack(List<List<Integer>> ans, List<Integer> track, List<Integer> nums) {
        if (nums.isEmpty()) ans.add(new ArrayList<>(track));
        else {
            int n = nums.remove(nums.size() - 1);
            //left branch
            //choose since choose empty, implicitly choose
            backtrack(ans, track, nums);
            //since choose empty, no need to remove
             
            //right branch
            track.add(n);
            backtrack(ans, track, nums);
            nums.add(n);  // when unchoose, we need to restore the original list
            track.remove(track.size() - 1);
        }
    }
}

第二种思路：每一次 我们选择不同的start index

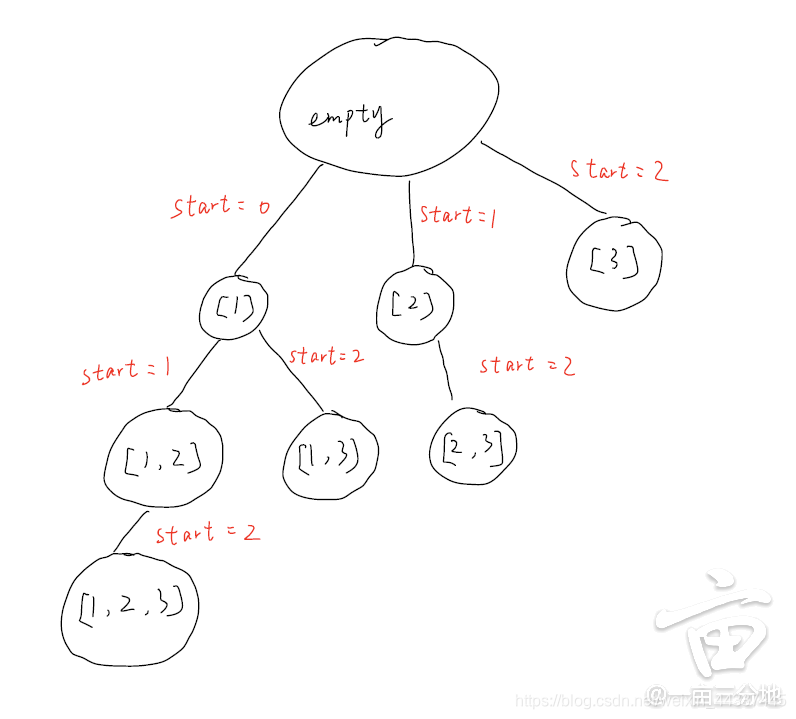
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> track = new ArrayList<>();
        backtrack(ans, track, nums, 0);
        return ans;
         
    }
     
    private void backtrack(List<List<Integer>> ans, List<Integer> track, int[] nums, int start) { //加入了start控制当前选层
        ans.add(new ArrayList<Integer>(track));
        for (int i = start; i < nums.length; ++i) {
            track.add(nums);
            backtrack(ans, track, nums, i + 1);
            track.remove(track.size() - 1);
        }
    }
}

LC113 Path Sum2

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<Integer> track = new ArrayList<>();
        List<List<Integer>> ans = new ArrayList<>();
        backtrack(root, sum, track, ans);
        return ans;
    }
     
    private void backtrack(TreeNode root, int sum, List<Integer> track, List<List<Integer>> ans) {
        if (root == null) return;
        if (root.left == null && root.right == null && root.val == sum) {
            track.add(root.val);
            ans.add(new ArrayList<>(track));
            track.remove(track.size() - 1);
        }
        else {
            track.add(root.val);
            backtrack(root.left, sum - root.val, track, ans);
            backtrack(root.right, sum - root.val, track, ans);
            track.remove(track.size() - 1);
        }
    }
}

LC51 N-Queens

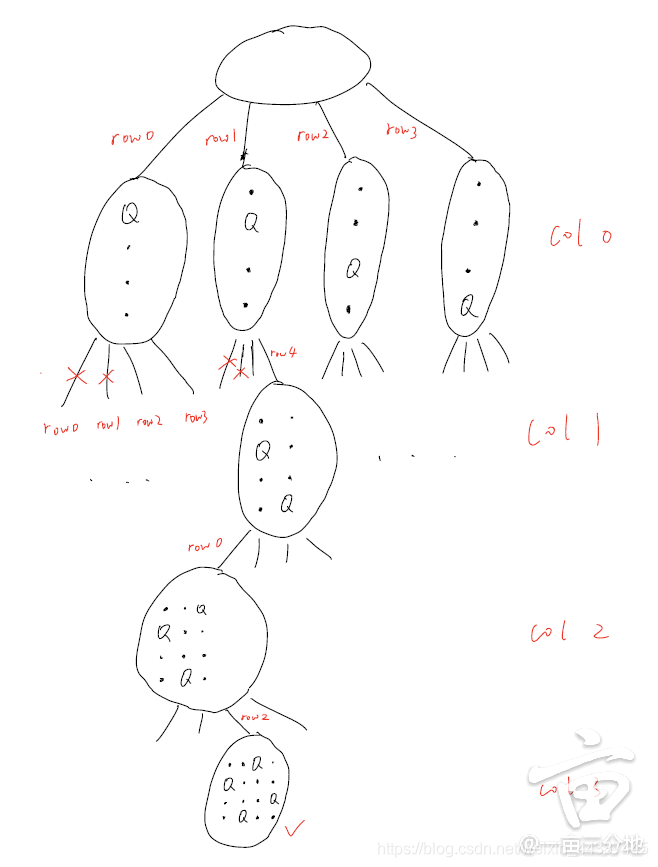
我们就是每一列，每个点去放置queen，看看是否可行。如果可行就继续，不可行就剪枝。
所以终止条件（base case）就是col == n的时候。
下面代码非常清晰

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> ans = new ArrayList<>();
        List<String> track = new ArrayList<>();
        char[][] board = new char[n][n];
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                board[j] = '.';
            }
        }
        backtrack(n, board, ans, 0);
        return ans;
    }
     
    private void backtrack(int n, char[][] board, List<List<String>> ans, int col) {
        if (col == n) ans.add(construct(board)); //终止条件
        else {
            for (int row = 0; row < n; ++row) { 
                if (isSafe(board, row, col)) { //对于当前的col 我们要检查每一个row是否合法
                    board[row][col] = 'Q';  // choose
                    backtrack(n, board, ans, col + 1); //explore
                    board[row][col] = '.';  // unchoose
                }
            }
        }
         
    }
    private boolean isSafe(char[][] board, int row, int col) { //检查是否合法的方式也很粗暴，就是检查同行有没有Q或者斜对行有没有Q
        for (int i = col - 1; i >= 0; --i) {
            if (board[row] == 'Q') return false;
            if (row + col - i < board.length && board[row + col - i] == 'Q')
                return false;
            if (row - col + i >= 0 && board[row - col + i] == 'Q')
                return false;
        }
        return true;
    }
     
     
     
    private List<String> construct(char[][] board) {
        List<String> track = new ArrayList<>();
        for (int i = 0; i < board.length; ++i) {
            track.add(new String(board));
        }
        return track;
    }
}

总结：
做这种题目 一定要做到心中有树。知道每一层我们将做出怎么样的选择。