基于 PyTorch 动手实现 LLM
本文是 Stanford CS336 课程学习记录的一部分。
撰写本文时,模型尚未经过训练,尽管模块可以通过测试,但可能仍然存在一些潜在问题。本文仅供参考。
概述
在 CS336 课程的作业 1 中,要求我们基于 PyTorch 框架自己实现一个 Transformer 语言模型并训练它。本文记录模型架构的实现。对着作业指导加上问大模型连滚带爬算是写了个大概,能通过所有测试了。
我们需要实现的是一个 Pre-Norm 的 Transformer 语言模型,带有现代 LLM 的常见优化:LayerNorm 前置、SwiGLU 激活、RMSNorm、无 bias 的线性层、旋转位置嵌入(RoPE)等。架构图如下:

具体来说,此模型的输入是经过分词器(Tokenizer,通常是 BPE)分词的 token ID 序列,输出是针对输入序列中每个 token,预测其下一个 token 的概率。
在我们的实际实现中,我们不会进行最后的 softmax 操作,而是直接返回 softmax 之前的张量,我们通常把这个张量称为 logits。
所有模块的实现
Linear 线性层
作业指导不允许我们使用 torch.nn.Linear,因此我们需要自己实现它。我们实现的是无 bias 的线性层,所以其实就是一个简单的矩阵乘法,没什么可说的,但是要注意一下参数初始化。
作业指导的 3.4.1 节指出,对于线性层的权重,我们使用以下的正态分布进行初始化:
这可以用以下代码实现:
sigma = math.sqrt(2 / (in_features + out_features))
w = torch.normal(mean=0, std=sigma, size=(out_features, in_features), device=device, dtype=dtype)
w = torch.nn.init.trunc_normal_(w, a=-3*sigma, b=3*sigma)
注意这里将权重矩阵初始化为 (out_features, in_features),因为作业指导中要求我们将矩阵存储为 \(W\) 而非 \(W^T\)。完成权重初始化后,只需只用 nn.Parameter 封装即可。
在 forward 函数中,我们使用 einx 的 dot 函数来完成矩阵乘法。在后面我们还会使用几次 einx,einx 可以视为 einops 和 einsum 的统一接口(可参考我之前写的一篇 einops 学习笔记),是终极张量操作库。
einx.dot("d_out d_in, ... d_in -> ... d_out", self.weight, x)
我们的权重的形状是 d_out d_in,输入张量 x 的形状是 ... d_in,... 在 einx 语法中表示 0 个或多个维度。最终输出的张量形状是 ... d_out。
Linear 的完整代码如下:
class Linear(nn.Module):
def __init__(
self, in_features: int, out_features: int, device: torch.device | None = None, dtype: torch.dtype | None = None
):
"""
Args:
in_features (int): final dimension of the input
out_features (int): final dimension of the output
device (torch.device | None = None): Device to store the parameters on
dtype (torch.dtype | None = None): Data type of the parameters
"""
super().__init__()
sigma = math.sqrt(2 / (in_features + out_features))
w = torch.normal(mean=0, std=sigma, size=(out_features, in_features), device=device, dtype=dtype)
w = torch.nn.init.trunc_normal_(w, a=-3*sigma, b=3*sigma)
self.weight = nn.Parameter(w)
def forward(self, x: torch.Tensor) -> torch.Tensor:
return einx.dot("d_out d_in, ... d_in -> ... d_out", self.weight, x)
Embedding 嵌入层
Embedding 其实是一个查表操作,这个表是可训练的,输入长度是 vocab_size,即模型的词表大小,输出长度一般是 d_model。
我们同样注意一下初始化。作业指导指出,Embedding 权重使用以下的正态分布进行初始化:
完整代码如下:
class Embedding(nn.Module):
def __init__(
self, num_embeddings, embedding_dim, device: torch.device | None = None, dtype: torch.dtype | None = None
):
"""
Args:
num_embeddings (int): Size of the vocabulary
embedding_dim (int): Dimension of the embedding vectors, i.e., d_model
device (torch.device | None = None): Device to store the parameters on
dtype (torch.dtype | None = None): Data type of the parameters
"""
super().__init__()
e = torch.normal(mean=0, std=1, size=(num_embeddings, embedding_dim), device=device, dtype=dtype)
e = torch.nn.init.trunc_normal_(e, a=-3, b=3)
self.weight = nn.Parameter(e)
def forward(self, token_ids: torch.LongTensor) -> torch.Tensor:
return self.weight[token_ids]
RMSNorm
对于向量 \(a\in \mathbb{R}^{d_\text{model}}\) 中的每个元素,RMSNorm 的公式如下:
其中
\(g\) 是一个可学习的参数向量(共有 \(d_\text{model}\) 个元素),\(\epsilon\) 是一个为了避免除以 0 的很小的常量,一般取 1e-5。
需要注意的是,在对输入取根号时,为了避免数值溢出,需要先扩大到 torch.float32 类型(考虑到实际训练中经常使用 FP16 或 BF16)。
RMSNorm 包含可学习的参数 \(g\),因此它应当被实现为 nn.Module 而不是一个无状态的函数。作业指导指出我们应当将 \(g\) 初始化为全 1 的张量。
完整代码如下:
class RMSNorm(nn.Module):
def __init__(
self, d_model: int, eps: float = 1e-5, device: torch.device | None = None, dtype: torch.dtype | None = None
):
"""
Args:
d_model (int): Hidden dimension of the model
eps (float = 1e-5) Epsilon value for numerical stability
device (torch.device | None = None) Device to store the parameters on
dtype (torch.dtype | None = None): Data type of the parameters
"""
super().__init__()
self.epsilon = eps
# 此处 d_model 后的逗号是必须的
g = torch.ones(size=(d_model,), device=device, dtype=dtype)
self.weight = nn.Parameter(g)
def forward(self, x: torch.Tensor) -> torch.Tensor:
# x 的形状是:(batch_size, seq_len, d_model)
# upcast input to torch.float32 to prevent overflow when square the input
in_dtype = x.dtype
x = x.to(torch.float32)
# RMSNorm implementation
# x 中所有元素的平方和
square_sum = einx.reduce("... [d_model]", x * x, op=torch.sum)
# x.shape[-1] 即为 d_model
rms = torch.sqrt(1 / x.shape[-1] * square_sum + self.epsilon)
rms = einx.rearrange("... -> ... 1", rms)
result = x / rms * self.weight
# Return the result in the original dtype
return result.to(in_dtype)
带有 SwiGLU 激活的 FeedForward 网络
SwiGLU 是 Swish 激活函数(也叫 SiLU)和线性门控单元 GLU 的结合。SiLU(Swish)激活函数公式如下:
其中 \(\sigma(x)\) 是 Sigmoid 函数。
下图展示了 SiLU(Swish)函数的图象。它与 ReLU 类似,但在 0 处更加平滑。
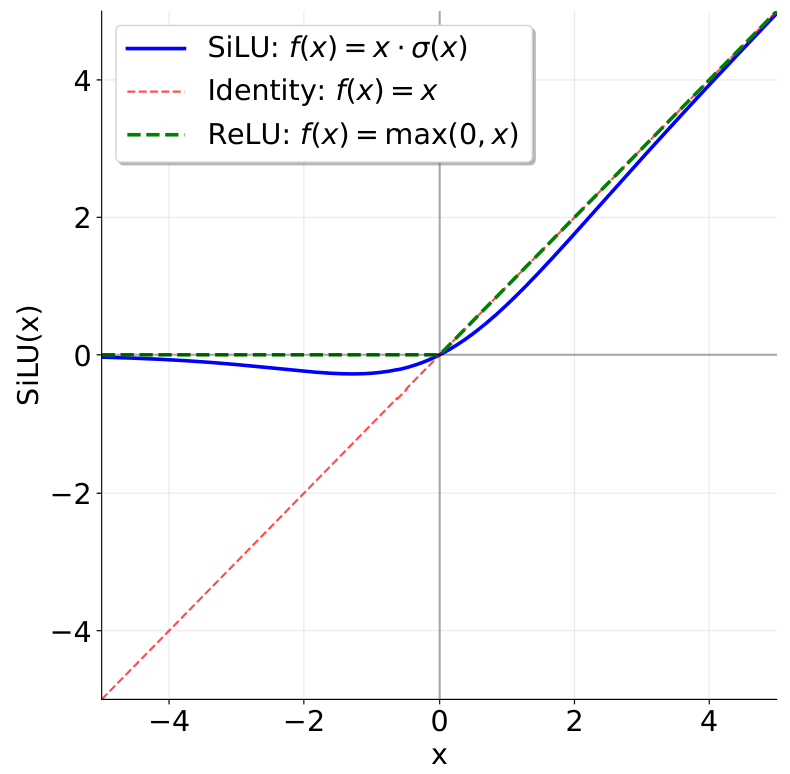
SiLU 可以使用以下代码实现。作业指导中指出,为了数值稳定性,我们应当直接使用 torch.sigmoid 来实现 SiLU。
def silu(x: torch.Tensor) -> torch.Tensor:
return x * torch.sigmoid(x)
GLU 公式如下:
其中 \(\sigma\) 是 Sigmoid 函数,\(\odot\) 表示逐元素乘法。\(W_1\) 和 \(W_2\) 是两个权重矩阵。
将二者结合起来,就得到了我们需要实现的前馈网络:
其中 \(x\in\mathbb{R}^{d_\text{model}},W_1,W_3\in\mathbb{R}^{d_\text{ff}\times d_\text{model}},W_2\in\mathbb{R}^{d_\text{model}\times d_\text{ff}}\)。一般我们令 \(d_\text{ff}=\frac{8}{3}d_\text{model}\),在实际实现中,为了充分利用硬件,通常取 \(d_\text{ff}\) 为最接近 \(\frac{8}{3}d_\text{model}\) 的 64 的整数倍。这可以通过以下代码实现:
def _get_d_ff(self, d_model: int) -> int:
# d_ff 应当大致等于 f_model 的 8/3。因此,我们首先将 d_model 乘以 8/3,然后将其四舍五入到最近的 64 的整数倍,从而充分利用硬件。
return int(round(d_model * (8 / 3) / 64) * 64)
我们的前馈网络应当包含 3 个线性模块,分别对应 \(W_1,W_2\) 和 \(W_3\)。完整代码如下:
class FeedForward(nn.Module):
"""
Position-wise feed forward network with SwiGLU activation
"""
def _get_d_ff(self, d_model: int) -> int:
# d_ff 应当大致等于 f_model 的 8/3。因此,我们首先将 d_model 乘以 8/3,然后将其四舍五入到最近的 64 的整数倍,从而充分利用硬件。
return int(round(d_model * (8 / 3) / 64) * 64)
def __init__(
self, d_model: int, d_ff: int = None, device: torch.device | None = None, dtype: torch.dtype | None = None
):
"""
Args:
d_model (int): Hidden dimension of the model
device (torch.device | None = None) Device to store the parameters on
dtype (torch.dtype | None = None): Data type of the parameters
"""
super().__init__()
self.d_model = d_model
self.d_ff = self._get_d_ff(d_model) if d_ff is None else d_ff
self.w1 = Linear(self.d_model, self.d_ff, device=device, dtype=dtype)
self.w2 = Linear(self.d_ff, self.d_model, device=device, dtype=dtype)
self.w3 = Linear(self.d_model, self.d_ff, device=device, dtype=dtype)
def forward(self, x: torch.Tensor) -> torch.Tensor:
# 此处不再使用 einx 了,因为需要访问 Linear 模块内部的权重,这样不太好。
w1x = self.w1(x)
w1x_silu = silu(w1x)
w3x = self.w3(x)
return self.w2(w1x_silu * w3x)
RoPE 旋转位置嵌入
这部分没搞太明白,代码算是 AI 写的,大概记录一下。
RoPE 的核心思想是,对于一个向量中的每一对维度(比如 \(i_{th}\) 位置的 \(q\) 向量的第 2k 和 2k+1 个维度),我们都对其应用一个二维旋转。这个旋转的角度 \(\theta_{i,k}\) 取决于:
- Token 在序列中的位置 \(i\)
- 维度对的索引 \(k\)
公式是 \(\theta_{i,k} = i / \Theta^{2k/d_k}\),其中 \(\Theta\) 是一个大常数(通常是10000),\(d_k\) 是向量总维度。
所以,对于一个输入查询向量 \(q\),其在位置 \(i\) 且维度为 \((2k, 2k+1)\) 的分量 \((q_{2k}, q_{2k+1})\) 会被旋转矩阵 [[cos( \(\theta_{i,k}\)), -sin( \(\theta_{i,k}\))], [sin( \(\theta_{i,k}\)), cos( \(\theta_{i,k}\))]] 作用。
RoPE 不包含任何可学习的参数,这意味着它是可以复用的。为了优化性能,我们在 RoPE 模块初始化时就预先计算出所有需要的 sin 和 cos 值,这样之后可以重复使用。
完整代码如下:
class RotaryPositionalEmbedding(nn.Module):
def __init__(self, theta: float, d_k: int, max_seq_len: int, device: torch.device | None = None):
"""
Args:
theta (float): theta value for the RoPE
d_k (int): dimension of query and key vectors
max_seq_len (int): Maximum sequence length that will be inputted
device (torch.device | None = None): Device to store the buffer on
"""
super().__init__()
# RoPE 本身不包含任何可学习的参数,__init__ 主要用来计算所有可能的位置 i 和所有可能的维度对 k 的 cos 和 sin 值,并存储起来,从而减少重复计算。
self.theta = theta
inv_freq = 1.0 / (self.theta ** (torch.arange(0, d_k, 2).float() / d_k)) # shape: (d_k // 2,)
position_indices = torch.arange(max_seq_len, dtype=torch.float) # shape: (max_seq_len,)
self.position_frequencies = einx.dot(
"inv_freq_len, max_seq_len -> max_seq_len inv_freq_len", inv_freq, position_indices
)
cos_cached = torch.cos(self.position_frequencies)
sin_cached = torch.sin(self.position_frequencies)
self.register_buffer("cos_cached", cos_cached, persistent=False)
self.register_buffer("sin_cached", sin_cached, persistent=False)
def forward(self, x: torch.Tensor, token_positions: torch.Tensor) -> torch.Tensor:
"""
Args:
x (..., seq_len, d_k)
token_positions (..., seq_len)
"""
current_cos = self.cos_cached[token_positions] # shape: (..., seq_len, d_k // 2)
current_sin = self.sin_cached[token_positions] # 同上
x_even = x[..., ::2] # shape: (..., seq_len, d_k // 2)
x_odd = x[..., 1::2] # 同上
rotated_x_even = x_even * current_cos - x_odd * current_sin
rotated_x_odd = x_even * current_sin + x_odd * current_cos
return torch.stack([rotated_x_even, rotated_x_odd], dim=-1).reshape(x.shape)
softmax
softmax 的公式如下:
注意,当 \(v_i\) 较大时,\(\text{exp}(v_i)\) 可能变成无穷大,从而分母也是无穷大,两个无穷大相除得到 NaN。由于对向量整体加上一个常量 \(c\) 不会影响 softmax 的结果,我们对向量整体减去向量中最大的元素,从而增加数值稳定性。
完整代码如下:
def softmax(x: torch.Tensor, dim: int):
"""
对输入张量 x 的第 i 个维度进行 softmax,通过减去目标维度中最大的值来增加数值稳定性。
Args:
"""
# keepdim=True 表示保持其他维度的值不变
max_val = torch.max(x, dim=dim, keepdim=True).values
x_stable = x - max_val
exp_x = torch.exp(x_stable)
exp_sum = torch.sum(exp_x, dim=dim, keepdim=True)
return exp_x / exp_sum
缩放点积注意力
于是我们来到 self attention 的经典公式:
此处与经典公式有一点不同:原公式中的 \(QK^T\) 在这里是 \(Q^T K\)。这是因为作业指导要求我们使用列优先顺序存储矩阵。如果我们使用 einx 或者 einsum,那么这通常不需要太多注意。
我们还需要支持一个额外的功能:Masking。mask 是一个 bool 类型的矩阵,对于值为 False 的位置,我们需要将对应值设为 -torch.inf。
完整代码如下:
def scaled_dot_product_attention(q: torch.Tensor, k: torch.Tensor, v: torch.Tensor, mask: torch.Tensor = None):
"""
Args:
q (batch_size, ..., seq_len, d_k)
k (batch_size, ..., seq_len, d_k)
v (batch_size, ..., seq_len, d_v)
mask (seq_len, seq_len)
Returns a tensor with shape (batch_size, ..., d_v)
The attention probabilities of positions with a mask value of True should collectively sum
to 1, and the attention probabilities of positions with a mask value of False should be zero.
"""
qk = einx.dot("... seq_len_q d_k, ... seq_len_k d_k -> ... seq_len_q seq_len_k", q, k)
d_k = q.shape[-1]
pre_softmax = qk / math.sqrt(d_k)
if mask is not None:
pre_softmax.masked_fill_(mask=~mask, value=-torch.inf)
post_softmax = softmax(pre_softmax, dim=-1)
return einx.dot("... seq_len_q seq_len_k, ... seq_len_k d_v -> ... seq_len_q d_v", post_softmax, v)
MultiHeadAttention 多头注意力
上面的缩放点积注意力描述了一个注意力头的计算。在多头注意力中,我们将所有注意力头的 Attention 拼接到一起,然后通过一个统一的 \(W_O\) 矩阵映射到最终的输出。
直观上每个头都拥有各自的 Q、K、V 映射矩阵。然而,为了减少计算量,我们使用统一的 Q、K、V 矩阵,然后在进行自注意力计算之前将它们拆分,最后再拼接起来。
我们还需要构建一个因果掩码矩阵,这可以通过 torch.tril 来实现。
完整代码如下:
class MultiHeadSelfAttention(nn.Module):
def __init__(
self,
d_model: int,
num_heads: int,
rope_max_seq_len: int = None,
rope_theta: int = None,
device: torch.device | None = None,
dtype: torch.dtype | None = None,
):
"""
Args:
d_model (int) Dimensionality of the Transformer block inputs.
num_heads (int) Number of heads to use in multi-head self-attention.
rope_max_seq_len (int = None) max_seq_len for RoPE. If None, will not use RoPE
rope_theta (int = None) theta for RoPE. If None, will not use RoPE
device (torch.device | None = None) Device to store the parameters on
dtype (torch.dtype | None = None): Data type of the parameters
"""
super().__init__()
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
# 使用整数除法来确保整除
d_k = d_model // num_heads
self.num_heads = num_heads
self.d_model = d_model
# 线性投影层
self.q_proj = Linear(d_model, d_model, device=device, dtype=dtype)
self.k_proj = Linear(d_model, d_model, device=device, dtype=dtype)
self.v_proj = Linear(d_model, d_model, device=device, dtype=dtype)
# 最终的输出层
self.output_proj = Linear(d_model, d_model, device=device, dtype=dtype)
if rope_max_seq_len is not None or rope_theta is not None:
assert rope_max_seq_len is not None and rope_theta is not None, (
"rope_max_seq_len and rope_theta must be not None to enable RoPE"
)
self.rope = RotaryPositionalEmbedding(
theta=rope_theta, d_k=d_k, max_seq_len=rope_max_seq_len, device=device
)
else:
self.rope = None
def forward(self, x: torch.Tensor, token_positions: torch.Tensor = None):
"""
Args:
x should be (batch_size, seq_len, d_model) in shape
token_positions should be (..., seq_len) in shape
"""
_, seq_len, _ = x.shape
q_proj = self.q_proj(x) # (batch_size, seq_len, d_model)
k_proj = self.k_proj(x) # 同上
v_proj = self.v_proj(x) # 同上
q = einx.rearrange(
"batch seq_len (num_heads head_dim) -> batch num_heads seq_len head_dim",
q_proj,
num_heads=self.num_heads,
)
k = einx.rearrange(
"batch seq_len (num_heads head_dim) -> batch num_heads seq_len head_dim",
k_proj,
num_heads=self.num_heads,
)
v = einx.rearrange(
"batch seq_len (num_heads head_dim) -> batch num_heads seq_len head_dim",
v_proj,
num_heads=self.num_heads,
)
# apply rope
if self.rope:
assert token_positions is not None, "token_positions is necessary when RoPE is enabled"
q = self.rope(q, token_positions) # (batch_size, num_heads, seq_len, head_dim)
k = self.rope(k, token_positions)
# scaled_dot_product_attention 对 mask 的要求:True 表示允许注意(不填充),False 表示需要掩盖(填充 -inf)。
# 对因果掩码而言,这意味着下三角(包括对角线)应该是 True,上三角应该是 False。
causal_mask = torch.ones((seq_len, seq_len), dtype=torch.bool).tril(diagonal=0)
attn_output_per_head = scaled_dot_product_attention(
q, k, v, mask=causal_mask
) # (batch_size, num_heads, seq_len, head_dim)
attn_output_combined = einx.rearrange(
"batch num_heads seq_len head_dim -> batch seq_len (num_heads head_dim)",
attn_output_per_head,
num_heads=self.num_heads,
)
return self.output_proj(attn_output_combined)
Transformer Block
Transformer Block 是 Transformer 语言模型的基本组成单位。Transformer 语言模型包含若干个层,每层是一个 Transformer Block。
Transformer Block 包含两个子层:MultiHeadAttention 子层和 FFN 子层。具体可以参考本文开头的图片。
MultiHeadAttention 子层计算可描述为以下公式:
FFN 子层计算可描述为以下公式:
注意这里的两个 RMSNorm 是不共享的,需要独立初始化。
前面的 RoPE 模块和所有用到 RoPE 的模块都需要 token_positions,经过查看作业提供的框架代码,这些模块在测试时都提供了现成的 token_positions,而 Transformer Block 在测试时却没有提供 token_positions。因此,我们需要手动构造它。
完整代码如下:
class TransformerBlock(nn.Module):
def __init__(
self,
d_model: int,
num_heads: int,
d_ff: int,
rope_max_seq_len: int,
rope_theta: int,
device: torch.device | None = None,
dtype: torch.dtype | None = None,
):
"""
Args:
d_model (int) Dimensionality of the Transformer block inputs
num_heads (int) Number of heads to use in multi-head self-attention
d_ff (int) Dimensionality of the position-wise feed-forward inner layer
rope_max_seq_len (int) max_seq_len for RoPE
rope_theta (int) theta for RoPE
device (torch.device | None = None) Device to store the parameters on
dtype (torch.dtype | None = None): Data type of the parameters
"""
super().__init__()
self.attn = MultiHeadSelfAttention(
d_model=d_model,
num_heads=num_heads,
rope_max_seq_len=rope_max_seq_len,
rope_theta=rope_theta,
device=device,
dtype=dtype,
)
# layer norm for sub-layer 1
self.ln1 = RMSNorm(d_model=d_model, device=device, dtype=dtype)
# layer norm for sub-layer 2
self.ln2 = RMSNorm(d_model=d_model, device=device, dtype=dtype)
self.ffn = FeedForward(d_model=d_model, d_ff=d_ff, device=device, dtype=dtype)
def forward(self, x: torch.Tensor):
# 构造 token_positions:[0, 1, 2, ..., seq_len-1]
_, seq_len, _ = x.shape # 输入形状是 (batch_size, seq_len, d_model)
token_positions = torch.arange(seq_len, device=x.device, dtype=torch.long)
# 执行包含两个子层的前向传播过程
sub_layer_1 = x + self.attn(self.ln1(x), token_positions)
sub_layer_2 = sub_layer_1 + self.ffn(self.ln2(sub_layer_1))
return sub_layer_2
完整的 Transformer 语言模型
终于到最后一步了。我们将会把之前实现的所有模块拼装起来,形成一个完整的 Transformer 语言模型。
通过本文开头的图片可以看到 Transformer 语言模型的计算步骤:
- 进行 Token Embedding,将分词器产生的离散 Token 序列转换成连续的嵌入向量。
- 嵌入向量依次通过所有 Transformer Block 形成的层
- 进行一次 RMSNorm
- 进行一次输出映射,算是 Token Embedding 的逆操作,将连续的向量映射到 logits。
我们的 Transformer 语言模型得到 logits 后就直接返回了。如果对 logits 再进行一次 softmax 操作,就能得到模型对下一个 token 在词表中的位置预测概率。
完整代码如下:
class TransformerLM(nn.Module):
def __init__(
self,
d_model: int,
num_heads: int,
d_ff: int,
vocab_size: int,
context_length: int,
num_layers: int,
rope_theta: int,
device: torch.device | None = None,
dtype: torch.dtype | None = None,
):
"""
Args:
d_model (int) Dimensionality of the Transformer block inputs
num_heads (int) Number of heads to use in multi-head self-attention
d_ff (int) Dimensionality of the position-wise feed-forward inner layer
vocab_size (int) The size of the vocabulary
context_length (int) The maximum context length
num_layers (int) The number of Transformer blocks to use
rope_theta (int) theta for RoPE
device (torch.device | None = None) Device to store the parameters on
dtype (torch.dtype | None = None): Data type of the parameters
"""
super().__init__()
self.token_embeddings = Embedding(num_embeddings=vocab_size, embedding_dim=d_model, device=device, dtype=dtype)
self.layers = nn.ModuleList(
[
TransformerBlock(
d_model=d_model,
num_heads=num_heads,
d_ff=d_ff,
rope_max_seq_len=context_length,
rope_theta=rope_theta,
device=device,
dtype=dtype,
)
for _ in range(num_layers)
]
)
# layer norm final
self.ln_final = RMSNorm(d_model=d_model, device=device, dtype=dtype)
# output embedding (a linear layer)
self.lm_head = Linear(d_model, vocab_size, device=device, dtype=dtype)
def forward(self, x: torch.Tensor):
token_embeddings = self.token_embeddings(x) # (batch_size, seq_len, d_model)
hidden_states = token_embeddings
for layer in self.layers:
hidden_states = layer(hidden_states) # (batch_size, seq_len, d_model)
post_norm = self.ln_final(hidden_states) # (batch_size, seq_len, d_model)
logits = self.lm_head(post_norm) # (batch_size, seq_len, vocab_size)
return logits



 浙公网安备 33010602011771号
浙公网安备 33010602011771号