文献阅读 | Novel approach for parallelizing pairwise comparison problems as applied to detecting segments identical by decent in whole-genome data

Sapin, Keller (2021) Novel Approach for Parallelizing Pairwise Comparison Problems as Applied to Detecting Segments Identical By Decent in Whole-Genome Data. Bioinformatics . http://dx.doi.org/10.1093/bioinformatics/btab084

在基因组学研究中，数据集已经十分庞大，并且在未来数据规模仍会进一步增加。因此，需要成对比较的问题（无论是成对的SNP或是成对的个体）在计算上都将极具挑战性。对此，作者提出了一个解决两两比较的通用算法，以将 \(n^2\) 规模的问题简化为多个复杂度为 \(n\) 小问题并能够并行进行。

目录

• 算法描述
• Benchmark

算法描述

本质上，作者的方法创新在于提出了一种近乎等大地划分子集的方法，从而将全部两两比较（\(n^2\)个）划分为等大的若干个子集进行运算，进而可以利用并行方法缩减时间。

首先，记所有构成一个个体的各项属性为 \(x_i, i \in \{1...n\} (n \geqslant 4)\)，因此对于任意成对个体，可记为 \(\{x_i, x_j\}\)。记 \(p\) 为最小质数，则有 \(p^2 \geqslant n\)。为了创建子集，从 \(1\) 至 \(p^2\)的数字被按列放置在一个 \(p \times p\)的矩阵 \(P\) 中（图一）。其中，数字 \(1...n\) 是样本中个体的下标，数字 \(n+1...p^2\) 是未被关联的（are unassociated (null)）而这将使一些子集拥有比其他子集更少的样本。

图1
Matrix \(P\), \(p_1\) and \(P_{p-1}\)
（第一行第一个矩阵为\(P\)，第二个为\(p_1\)，第三个为\(p_2\)， 第二行第一个为\(p_3\)，第二个为\(p_4\)。显然，\(p\)是\(5 \times 5\)的矩阵，因此\(p=5\)。）

如此一来，作者的方法即可产生 \(p^2 + p \approx n + \sqrt{n}\)个独立的子集。其中，第一个\(p\)子集由矩阵\(P\)的每一列定义，而下一个\(p\)子集由矩阵\(P\)的每一行定义，即共有\(2p\)个子集被从矩阵\(P\)中提取出来。举个例子，基于矩阵\(P\)的行定义的最后一个子集将包括个体\(x_p, x_{2p}, x_{3p}, ..., x_{p^2}\)。

剩余的 \(p^2 + p - 2p = p^2 - p\) 个子集，则由新矩阵\(P_k\)所定义。每个矩阵\(P_k (k \in \{1...p-1\})\)都是通过移动矩阵\(P\)的列中的元素得来的。与之前\(2p\)个从矩阵\(P\)中产生的子集不同，基于\(P_k\)产生的子集仅由\(P_k\)的行（而非列）所定义。因此，每个\(P_k\)矩阵贡献了\(p\)个额外的子集。为了生成这\(p-1\)个\(P_k\)矩阵，\(P_k\)中的每一列\(i\)中的每个元素都相对于\(P\)中的\(i\)被向上移动了\(r(i,k)\)行，并有：

\(r(i, k) = ((i - 1) \times k) \,\,\,\, mod \, p\)

其中，\(mod\)为取模。举个例子，对于\(k=1\)，则有\(r(i=1, k=1)=0\)，因此\(P_1\)的第一列不做移动与\(p\)的第一列保持一致；\(r(i=2, k=1)=1\)，因此P_1\(的第二列中的元素相较于P\)中的上移了一个元素；\(r(i=3, k=1)=2\)，因此P_1\(的第三列中的元素相较于P\)中的上移了两个元素，以此类推。

总之，产生的子集共有\(p^2+p\)个（其中，\(2p\)个是由原始矩阵\(P\)生成的，剩下的是由矩阵\(P_k\)生成的），每个个体都出现在了\(p+1\)个不同子集中，而每个子集中的个体数为\(p\)（或者少于\(p\)，在\(p^2>n\)的情形下）。图2展示了当\(n=p^2=25\)时的矩阵\(P\)、\(P_1\)、\(P_2\)、\(P_3\)和\(P_4\)。

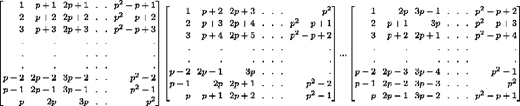
图2
Matrices \(P\), \(P_1\), \(P_2\), \(P_3\) and \(P_4\) for \(n=p^2=25\)

为了验证这一方法的准确性，作者计算了每一种样本对出现在同一子集中的次数\(t\)。经过对所有\(n<5M\)的模拟，作者发现每一种样本对均出现且仅出现在一个子集中。虽然没有严格的公式证明，但根据这一模拟结果，至少在\(n<5M\)的范围内，作者验证了其提出的方法是正确的，并且“没有理由怀疑该算法在\(n>5M\)时会表现得不一致”。因此，这些子集形成了一个仿射平面，其中子集是直线，子集中的个体是直线上的点。

不包括自我比较，根据作者提出的方法进行的比较总数是\(\frac{p^4-p^2}{2}\)，是\(p^2+p\)子个集和每个子集内部\(\frac{p^2-p}{2}\)次比较的乘积。在naive方法下，整个数据集中的每一对个体都进行比较的话，总数是\(\frac{n^2-n}{2}\)。因此，在\(p^2=n\)的最佳情况下，作者提出的方法同native方法具有相同的运算次数，但可以进行并行化处理从而提升速度。类似地，如果包括自我比较，并仅对前\(p\)个子集执行这些比较以避免多次自我比较，再次导致与native方法相同的比较次数。GitHub页面位于https://github.com/emmanuelsapin，使用代码生成组成每个子集的个体ID列表。

Benchmark

假设对可以同时并行运行的任务数量没有限制，并且运算时间与比较次数成正比（1:1），作者提出的方法应该将成对比较问题所花费的时间减少n倍（即从\(n^2\)变成\(n\)）。这是由于作者的方法使得每个子集内部进行了$\approx \frac{p^2}{2} \approx \frac{n}{2} \(次比较，而标准方法则是在全部样本中进行了\)\approx \frac{n^2}{2}$次比较。

接着，作者讨论了实际运行环境中，并不一定能达到缩减\(n\)倍的理想效果，因为并行运算的作业调度、IO限制等都会导致实际运行时间的增长。

为了量化作者的方法在实际问题上的表现，作者采用了UK Biobank data中的部分样本（从\(n=100\)到\(n=435187\)，即整个数据集）进行IBD比较。比较采用了GERMLINE软件。同时，由于比较次数为\(n^2\)的传统方法需要的内存（约2.4TB）和时间（约1年）太大太长，作者只能以较小样本估计整个数据集两两比较时所需时间。

为了进行作者所需的并行运算，作者采用了University of Colorado at Boulder的运算集群the Blanca Condo Cluster。同时，作者对GERMLINE软件进行了“minor modification”以减少硬盘读写次数，并表示这一改动使得“文件读取操作的总数减少了三个数量级”。

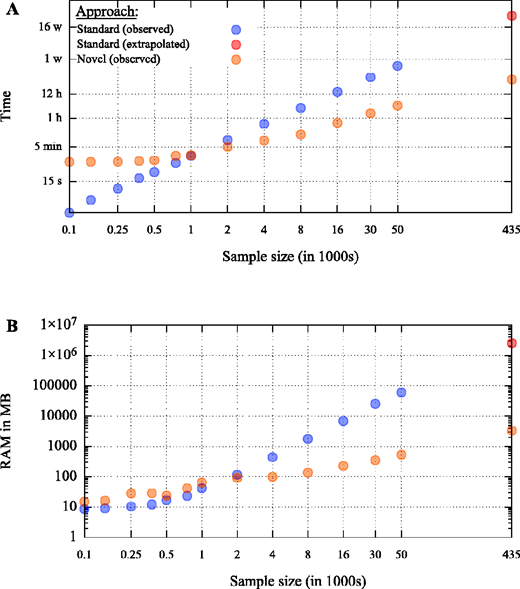
图3
两种方法用时（A）和内存占用（B）的比较。