文献阅读 | Genomic prediction of maize yield across European environmental conditions

Millet, E.J., Kruijer, W., Coupel-Ledru, A. et al. Genomic prediction of maize yield across European environmental conditions. Nat Genet 51, 952–956 (2019). https://doi.org/10.1038/s41588-019-0414-y

作者提出了一种在基因型与环境互作下，种质资源评估的新策略，并对玉米的籽粒重、籽粒数进行了建模。作者采用的大规模的传感器网络进行环境参数测量，且田间试验覆盖较为广泛，并通过加入对玉米生长期的考虑首先鉴定了环境对籽粒重、籽粒数的不同影响。

传感器网络的发展为成千上万领域的环境表征开辟了新的途径。在基因与环境互作条件下，小组提出一个新的种质评价方法。产量分析包括粒重和粒数以及基因环境交互被建模为对环境驱动因素的基因型敏感性。环境的特征在于根据每个田地中的传感器数据计算的基因型特异性指数以及在表型平台上针对每种基因型校准的物候学的进展。采用全基因组回归方法进行基因型敏感性分析，可以准确预测基因型与环境交互条件下的产量,超过基准的方法。

目录

• 基本介绍
• 简略流程与结果
• 基因组预测模型
• 环境效应预测

基本介绍

产量相关基因/QTL在不同环境下表现有所不同（基因型与环境互作，G × E），因为在不同环境下，相关等位基因具有正、负或零效应。进化限制了生理过程之间的相互作用，使得像粒数这样的综合成分性状以相对简单的方式对环境条件的变化作出反应。因此，产量的G × E问题可以通过研究在不同环境条件下影响相关表型的遗传因素来解决。产量的敏感性主要随胁迫时间的变化而变化。

现在可以根据标记谱和环境指数来预测许多玉米品种的开花时间，并且在当前和未来的气候条件下，可以根据整个欧洲的一系列玉米基因型模拟物候事件的日期。

作者首先鉴定了产量组成性状在G × E中的环境驱动因素，然后根据标记信息预测相应的基因型对所测环境条件的敏感性（补充图1），来解决产量的基因组预测问题。利用表型平台上的数据预测植物物候是构建基因型特异的环境特征的关键。作者称其方法比使用环境相关性矩阵和遗传亲缘关系矩阵的最先进的基因组预测方法要好。

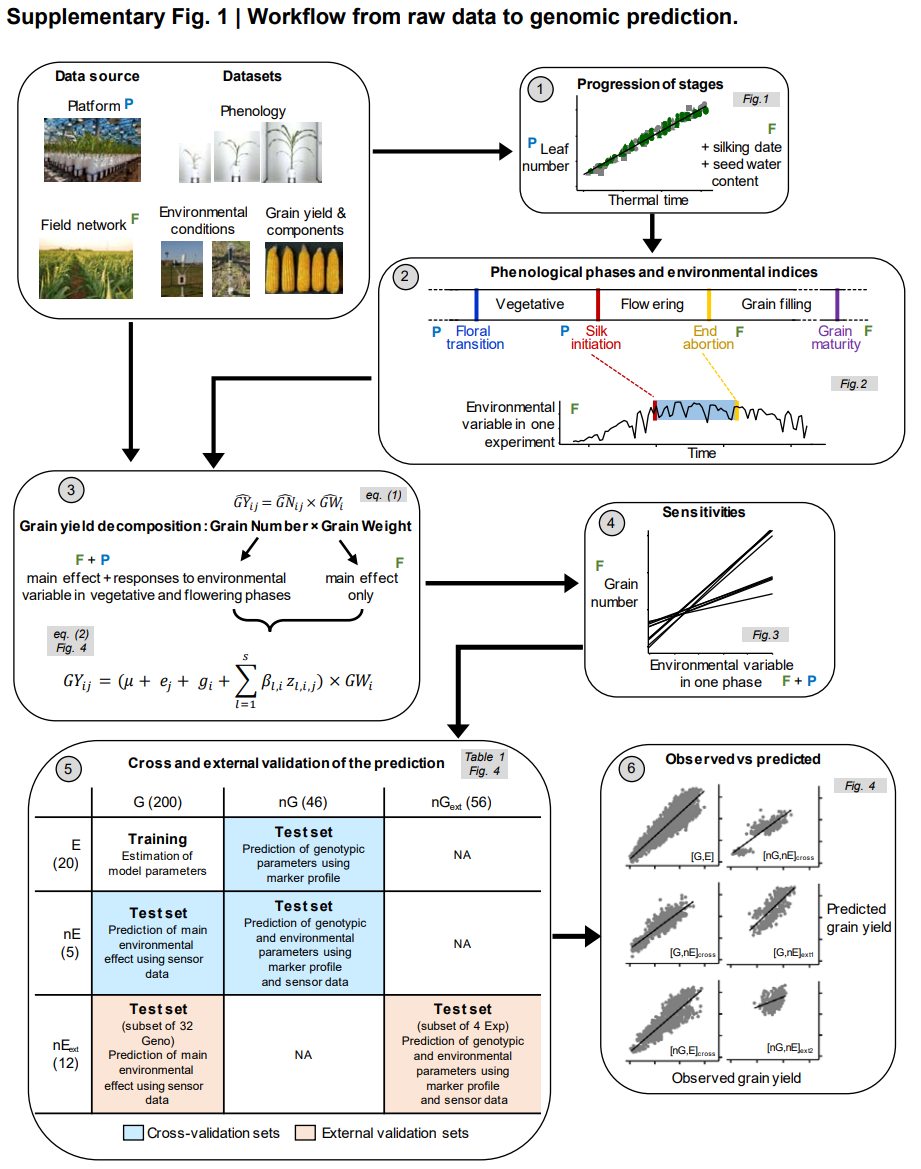
简略流程与结果

在25个田间试验中，在雨水和灌溉条件下，沿着西欧至东欧的气候样地，和智利进行了一项试验，对246个dent maize杂交种的多样性单产进行了测量（图1a）。产量在不同实验之间强烈变化（例如1.2–12.9 t/ha作为参考杂交种）和杂交（例如 2.1–7.1 t/ha在一个实验中）。其与整个实验中的籽粒数密切相关（例如，参考杂种的r = 0.96）。

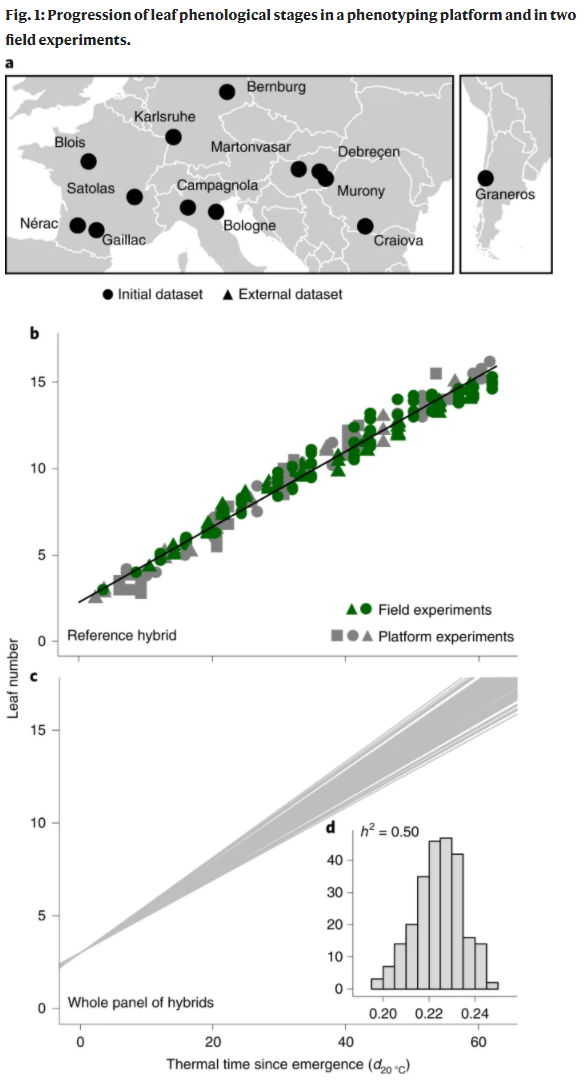
作者首先建模了每个田间杂交种叶片物候期的进程，因为直接评估繁殖事件的时间是不可行的。这是基于在一个机器人化表型平台上进行的测量。叶数增加的进程与热时间（thermal time）密切相关（校正了分生组织温度的影响），对于参考杂交种，与田间观察结果一致（图1b）。物候期进展速度呈现明显的基因型差异（图1c,d）。在每个位点，根据热时间和温度记录计算所有杂交种的叶期日期。

叶期的进展允许对所有杂种估计定义三个物候期的四个物候事件的日期（图2；补充图2）：
1）第一阶段（下文称为“vegetative”）从顶端花期过渡到卵巢上的绢丝萌发。这两个事件未直接测量，但严格对应于在表型平台中观察到的叶期。
2）开花期（The flowering phase）从开始抽雄到谷物不能提前终止（grains cannot abort）为止。
3）灌浆期（The grain-filling phase），从流产结束（from the end of abortion）到生理成熟为止的籽粒充实阶段21。

杂种之间发育时间不同，因此在每个物候期都在同一田地经历不同的环境条件（图2a–c）。这些条件差异产生了广泛的基因型特异性截获辐射（genotype-specific intercepted radiation）（\(R_{int}\)），土壤水势（\(\Psi _{soil}\)）和分生组织温度。

然后，作者检查了产量成分（数量和重量）与环境条件之间的关系（图3）。根据植物在营养期截获的辐射量（\(R_{int}\)）、开花期的平均夜间温度（\(T_{night}\)）（就像在小麦和水稻中）以及开花期的土壤水势（\(\Psi _{soil}\)），观察到了粒数的G × E。例如，\(T_{night}\)增加3°C时会使粒数降低15至50%（从最不敏感的杂种到最敏感的）。单粒均重并不依赖于在开花后的阶段，符合之前关于灌浆鲁棒性的研究结果（除了在极端条件下）。因此，它被认为是仅依赖于基因型的，并且使用非G×E模型进行估计。

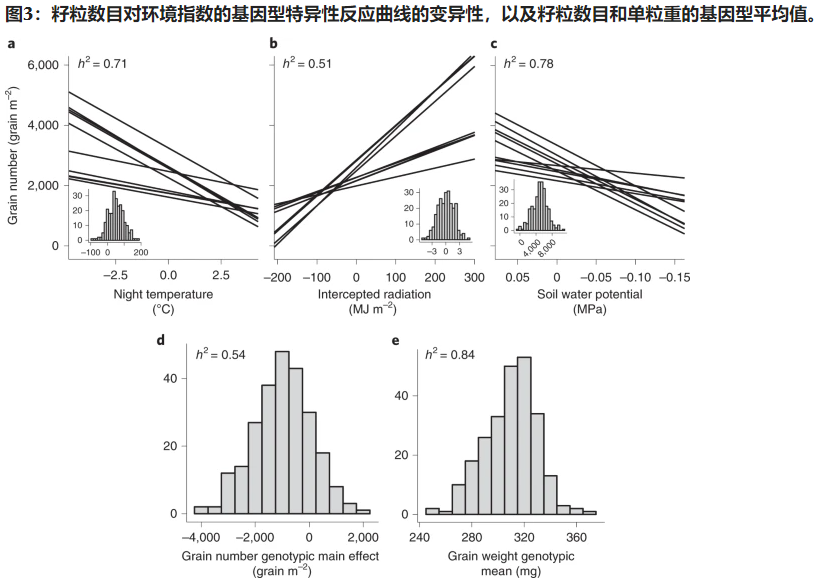
第\(i\)个杂种在第\(j\)个环境的产量\(\widehat{GY_{i,j}}\)被建模为个体的估计粒重\(\widehat{GW_{i}}\)和籽粒数\(\widehat{GN_{i,j}}\):

\[\widehat{GY_{i,j}} = \widehat{GW_{i}} \times \widehat{GN_{i,j}} \]

\(\widehat{GN_{i,j}}\)被进一步拆分为因子回归：

\[GN_{i,j} = \mu + e_j + g_i + \beta _{1,i}T_{night_{i,j}} + \beta _{2,i}R_{int_{i,j}} + \beta _{3,i}\Psi _{soil_{i,j}} + \varepsilon _{i,j} \]

其中：
1）\(\mu\)是截距
2）\(e_j\)和\(g_i\)是环境和基因型的主要效应，\(\varepsilon _{i,j}\)是残差
3）\(\beta _{1,i}\)，\(\beta _{2,i}\)和\(\beta _{3,i}\)是基因型决定的、对环境的敏感性系数
4）\(T_{night_{i,j}}\)，\(R_{int_{i,j}}\)和\(\Psi _{soil_{i,j}}\)是第\(i\)个杂种在第\(j\)个环境的测定值

敏感性表现出较大的基因型变异性和较高的狭义遗传力，h² = 0.51 – 0.78

通过上述两公式预测的产量，与单位点分析观测到的基因型均值呈现清晰的关联性：
1）各环境下，杂种间r = 0.60 – 0.91
2）特定杂种在各环境间 r = 0.71 – 0.97

然后，作者使用前述两方程来预测未观察到的环境和/或杂种的谷物产量（图4）。使用与描述G×E相同的环境指数（\(e_j\)）（根据传感器数据计算）来预测环境主要影响。基因型特异性参数（关于粒重的\(GW_{i}\)，和关于粒数的\(g_i\)、\(\beta _{1,i}\)、\(\beta _{2,i}\)、\(\beta _{3,i}\)）是从标记信息（marker profile）通过全基因组回归预测的（补充图3A-E）。根据传感器数据和基因组预测对叶型进程和开花时间进行计算，得出特异于基因型的环境指数（补充图3f–h）

b.模型参数，估计或预测取决于杂交种和试验是作为训练集（分别是G和E）还是测试集（分别是nG和nE）。对于已经测试过的G和E（浅蓝色格子），参数是通过粒数的因子回归（方程（2））从测量数据中估计出来的，或者是在整个实验中平均粒重。对于nE（绿色格子），利用测量的环境数据预测环境的主要影响。对于nG（洋红色格子），用基因组预测模型预测基因型参数。

c.第一个交叉验证样本（交叉验证集或外部验证集）每个数据集中预测和观察到的谷物产量之间的关系。在第一列中，总体相关性用杂交种和试验的线性回归表示（黑线）。第二列显示了与第一列相同的相关性，其中每个实验都用不同颜色表示。黑色虚线表示平分线。实验场编号如补充表1所示。

在交叉验证方案下，对杂交种和实验进行分层随机抽样，来评估预测准确性。作者从最初的246×25数据集中抽取了10次随机训练集，由200个杂交种（G）和20个实验（E）组成。剩下的46个杂交种（nG）和5个实验（nE）作为测试集，采用分层策略来尊重遗传群体的比例和环境情景。最后，我们使用来自外部环境和/或外部杂种的独立数据集进行了外部验证，评估了我们方法的预测性能（表1；补充图1；方法）。此外，我们通过将其与通过环境亲缘关系对G×E进行建模的基因组预测方法进行比较来对我们的方法进行基准测试。

• 对于在已有杂交种+新试验环境下\((G，nE)_{cross}\)的预测，观测和预测的籽粒产量之间的相关系数为 r = 0.43 – 0.85（环境一定、杂交种之间的r范围）和r = 0.71 – 0.9（杂种一定、环境之间）。
• 对于训练环境+新杂种 \((nG，E)_{cross}\)，每个试验的相关系数为 r = 0.21 – 0.71（杂种间）和r = 0.66 – 0.9（环境间）。相比之下，对于同一个数据集，使用环境-亲缘关系的基准方法得到的预测结果较差，每个实验的r = −0.12 – 0.44
• 对于新环境+新杂交种\((nG，nE)_{cross}\)，作者声称其方法产生了中等至良好的预测：每个实验环境下，不同杂种间 r = 0.20 – 0.74
• 对于已经训练过的杂交种+外部实验\((G，nE)_{ext1}\)，作者得到了中等到高度的相关性，r = 0.38 – 0.80（杂种间）和 r = 0.55 – 0.83（环境间）。对于第二组，外部试验环境+外部新杂交种\((nG，nE)_{ext2}\)，预测产量和观察产量之间的相关性在r = 0.32 – 0.39（杂种间）之间，尽管存在明显的偏差（图4；补充表1和表2）。

值得注意的是，作者的分析是在开花窗口期减少的情况下进行的，因此预测并不是由通过累积光合作用和避免胁迫对开花时间产量的巨大影响驱动的。同样，群体的遗传结构对预测的影响有限。

基因组预测模型

作者考虑了一组共8个基因型特征。5个来自产量分析（两个方程），即籽粒数量的基因型主效应、三种基因型敏感性和基因型平均粒重；另三个来自平台或田间的测量，用于定义每个杂种的物候期，即叶片出现率，丝化日期和最终叶片数。

对 \(g_i\) 效应的估计，作者采用了ByaesR，以全基因组回归模型进行基因组预测。

根据线性回归模型，上述性状与基因型标记数据通过线性模型 \(y = 1_n \mu + X \beta + \varepsilon\) 相关，其中 \(y\) 是待预测变量，\(X\) 是 \(n \times m\) 的SNP基因型矩阵，被编码为0，1和2（参考等位基因的拷贝数），\(\beta\) 是 \(m \times 1\) 的SNP效应向量。对于每个SNP的效应，ByaesR使用一个先验分布，即一个由四个均值为0的正态分布构成的混合模型：

\[\pi_1 \times N(0, 0 \times \sigma^2_g) + \pi_2 \times N(0, 10^{-4} \times \sigma^2_g) + \pi_3 \times N(0, 10^{-3} \times \sigma^2_g) + \pi_4 \times N(0, 10^{-2} \times \sigma^2_g) \]

其中，\(\pi_1\)，\(\pi_2\)，\(\pi_3\)和\(\pi_4\)分别表示一个SNP不具有，小，中或大效果的的概率。

作者运行了60000次MCMC迭代，包括a burn-in period of 10,000 and used a thinning rate of 10。

环境效应预测

新实验环境（nE）的环境的主效应\(e_j\)是基于训练集（E）估计的。估计基于下述方程：

\[\widehat{e_j} = a_2T_{night_j} + a_1R_{int_j} + a_3 \Psi_{soil_j} + \varepsilon_j \]