快速幂

快速幂

幂

当前博客只讨论幂数为整数的情况

幂是数学中的概念，比如要计算11的5次幂，其本质上就是5个11相乘得到的结果：

对于数学中的概念

• 任意一个数字的0次幂都等于1
• 一个数字的负n次幂都等于 1 / 该数的n次幂
• 一个数字的正n次幂等于n个该数字相乘

当然，我们也可以很容易得到如下代码

// x表示这个数字，n表示n次幂
public static double pow(int x, int n){
    // 如果该数为0
    if(x == 0)return 0;
    // 如果幂数是负的
    if(n < 0){
        return 1.0 / powProcess(x, -n);
    }else{
        // 如果幂数是正的
        return powProcess(x, n);
    }
}
public static double powProcess(int x, int n){
    // 基数为1，因为我们知道即便是极限情况一个数为0次幂，则结果也必定为1。且1和另一个数相乘一定会得到另一个数
    double res = 1;
    // 当n不为0的时候，就知道我们已经对x相乘n次了
    while(n != 0){
        // 当res第一次和x相乘，得到x，也就是x的1次幂
        res *= x;
        // n减少表示已经相乘过一次了
        n--;
    }
    return res;
}

对于上边的代码，结果是正确的。但是对于计算机来说这太浪费，每次都干几乎同样的事情(和x相乘)n次，我们希望有一种更高效的方法来解决冗余的操作。

快速幂

对于11的5次幂，这个例子来说，我们可以把5看作是一个二进制数(101)，将每个二进制所代表的幂求出来，然后再将式子进行汇总，那么我们就能得到最终的结果，变换如下图：

请注意这里的二进制的实际数值就表示了有几个x相乘，比如0101，其中0100表示的是4，那么就代表有4个x相乘，而0001表示的就是1个4相乘

详细变化如下，这里因为任何数的0次幂为1，所以中间那一项的结果为1，5的二进制为101所以可以这么进行转换：

因为二进制的某一位 i ( i 从第二位开始)，总是i - 1的2倍，所以我们对于上方转换的公式来说我们可以直接通过二进制的位数计算出来，这意味着我们只需要计算n的二进制位数那么多次就可以得到结果，代码如下：

public static double quickPow(int x, int n){
    if(x == 0)return 0;
    if(n < 0){
        return 1.0 / quickPowProcess(x, -n);
    }else{
        return quickPowProcess(x, n);
    }
}
public static double quickPowProcess(int x, int n){
    double res = 1.0;
    while(n > 0){
        // 只有二进制位为1的时候我们才知道这个位是有意义的
        if ((n & 1) == 1){
            // 将结果乘以当前x也就是相当于取出了有效的幂结果
            res *= x;
        }
        // x每次相乘都相当于是二进制位幂数的递增
        x *= x;
        // n的位数我们已经看过了，所以此时n的最后一位就没有意义了，因为我们总是关心n的最后一位
        n = n >> 1;
    }
    // 最终n的二进制位数上全是0，此时我们知道我们已经计算出了所有的有效位，所以返回结果
    return res;
}

图详解如下，先在图上画出初始数据如下，注意这里的n直接表示成了二进制形式：

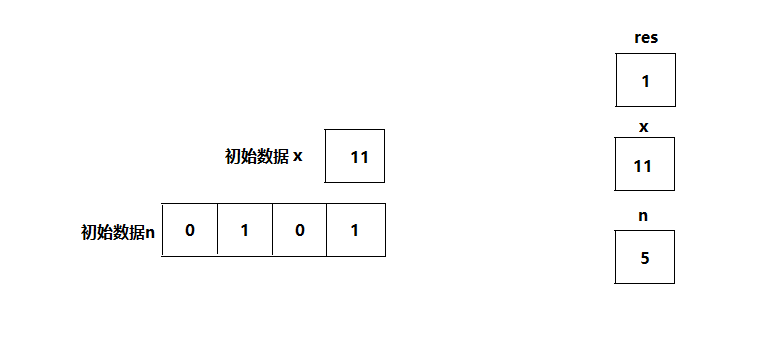
步骤如下：

• n与1做&操作 -->结果为1
• 若结果为1，res与x相乘 -->第一步成立，所以执行
• x自乘、n右移一位

自乘的意义就是得到前一位的幂结果，如：11 * 11，其实就是得到了11^{2的结果，而，11}2 * 11^{2结果就是11}4，以此类推

• n与1做&操作 -->结果为0
• 若结果为1，res与x相乘 -->第一步不成立，所以不执行
• x自乘、n右移一位

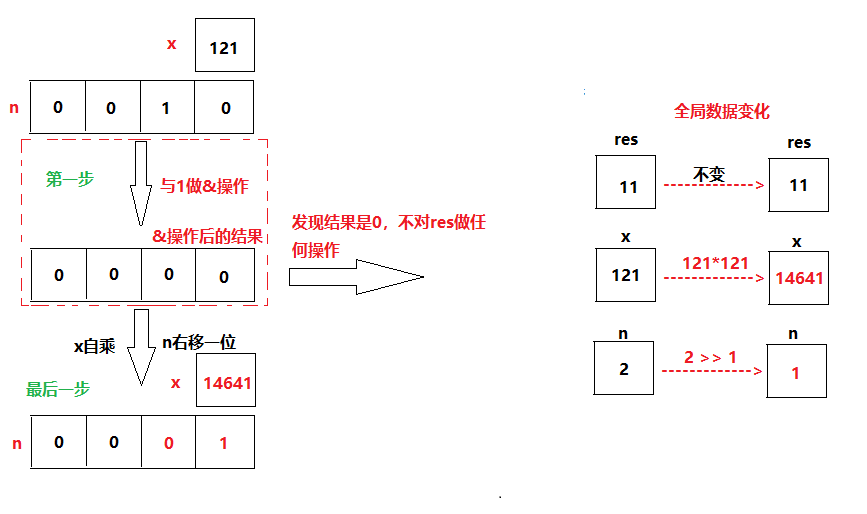
• n与1做&操作 -->结果为1
• 若结果为1，res与x相乘 -->成立，所以执行
• x自乘、n右移一位

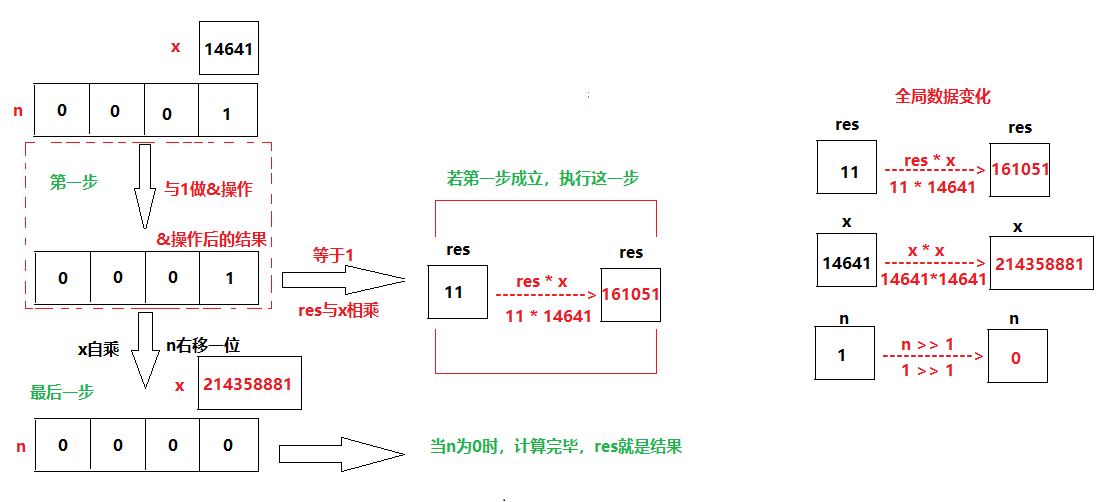
然后我们发现n已经为0了，这时再做任何操作都是无意义的了，所以计算完毕，而res就是最后的计算结果

通过两个数值的右移，我们搞定了原有方式可能会比较繁琐的代码

如果没有这些技巧，那么可能写出这样的代码：

public static double otherQuickPowProcess(int x, int n){
    double res = 1.0;
    // base为位移位数
    int base = 0;
    // base<防止越界 并且 1 左移base位后一定是小于等于n的 --Java中int类型只有32位，所以控制最大位移位数为31
    while(base < 32 && (1 << base) <= n ){
        // 提取目标位是否为1
        if (((1 << base) & n) != 0){
            res *= x;
        }
        x *= x;
        // 下次要多移动1位
        base++;
    }
    return res;
}

总结来说，计算一个数的n次幂，我们的计算次数不会超过log2(n)次，当n非常大时，性能会有显著提升，假如n为2万时，我们只需要计算最大log2(20000) + 1次，大约是15次

取模运算

对于幂运算，是很容易发生数值溢出的，所以一般在刷题或者面试题等算法相关问题上，都会出现类似取模运算，如：

• 对于任意的int类型x，求x的n次幂取模20000003(很大的一个素数)的结果

对于这类问题，不能先计算x的n次幂，因为会导致int类型溢出，先看代码：

public static double quickPow(int x, int n, int mod){
    if(x == 0)return 0;
    if(n < 0){
        return 1.0 / quickPowProcess(x, -n, mod);
    }else{
        return quickPowProcess(x, n, mod);
    }
}
public static double quickPowProcess(int x, int n, int mod){
    double res = 1.0;
    x = x % mod;
    while(n > 0){
        if ((n & 1) == 1){
            res = res * x % mod;
        }
        x = x * x % mod;
        n = n >> 1;
    }
    return res;
}

为什么直接对可能产生溢出的地方取余mod就行了呢？

可以看作每次mod操作其实都是在把装不下的东西给丢弃掉，但本身计算的结果并不会因为mod操作而产生数据丢失，对每一步超出mod值的步骤做mod操作都不会产生数据丢失问题，而对于本身不超过mod的数值做mod操作后，得到的就是自己，举个栗子：

比如我们要mod的数值是103，x为11，n为5，计算的结果存在res变量中

• 不做mod操作的例子

  • x&1结果为1，res与x相乘，res=11.0
  • x自乘等于121，n右移
  • x & 1结果为0，跳过
  • x自乘等于14641，n右移
  • x & 1结果为1，res与x相乘，res=161051
  • x自乘等于214,358,881，n右移
  • n等于0，结束

• 做mod操作的例子

  • x先%103，结果依旧是11，因为没有超过103
  • x&1结果为1，res与x相乘，res=11.0，res%103，数据保持原状
  • x自乘等于121，然后%103，因为是超过了，所以数据被截断变成了18，n右移
  • x & 1结果为0，跳过
  • x自乘等于324，然后%103，因为是超过了，所以数据被截断变成了15，n右移
  • x & 1结果为1，res与x相乘，res=165，res%103，数据被截断变成了62
  • x自乘等于225，然后% 103，因为超过了，所以数据被截断变成了19，n右移
  • n等于0，结束

而161051 % 103的值正是我们第二步算出的res值

但其实这份代码依旧是会有溢出的风险的，你知道是哪一步吗？(狗头)

递归快速幂

递归快速幂只是快速幂的递归实现，因为要额外使用方法栈空间来进行递归调用，且最优时间复杂度与迭代版本一致，所以我们一般更青睐于迭代版本

这里就直接给出公式以及代码了，根据公式还原代码，这很简单

根据公式还原代码

public static double quickPow(int x, int n){
    if(x == 0)return 0;
    if(n < 0){
        return 1.0 / quickPowProcess(x, -n);
    }else{
        return quickPowProcess(x, n);
    }
}
public static double quickPowProcess(int x, int n){
    // 说明是奇数
    if(n == 0){
        return 1.0;
    }else if(n & 1 == 1){
        // 奇数情况
        return quickPowProcess(x, n - 1);
    }else{
        // 偶数情况
        int tmp = quickPowProcess(x, n / 2);
        // 这么写时间复杂度就是O(N)了
        // return quickPowProcess(x, n / 2) * quickPowProcess(x, n / 2);
        return tmp * tmp;
    }
}