数据结构-线性表
线性表概述
概念
线性表,顾名思义就是具有线一样性质的表,该表中的内存空间是连续的,就像线一样。
定义:零个或多个数据元素的有限序列。
例子1:星座的排列。我们总是把星座按如下顺序排列:
白羊座、金牛座、双子座、巨蟹座、狮子座、处女座、天秤座、天蝎座、射手座、摩羯座、水瓶座、双鱼座
每个元素与相邻的元素都有联系,这排列顺序也是不可打乱的,这个顺序是按照月份来计算的,你不能去改变这样的关系。
例子2:食堂买饭排队(这里假设排队的人都很有素质,大家都在排队区排队)。
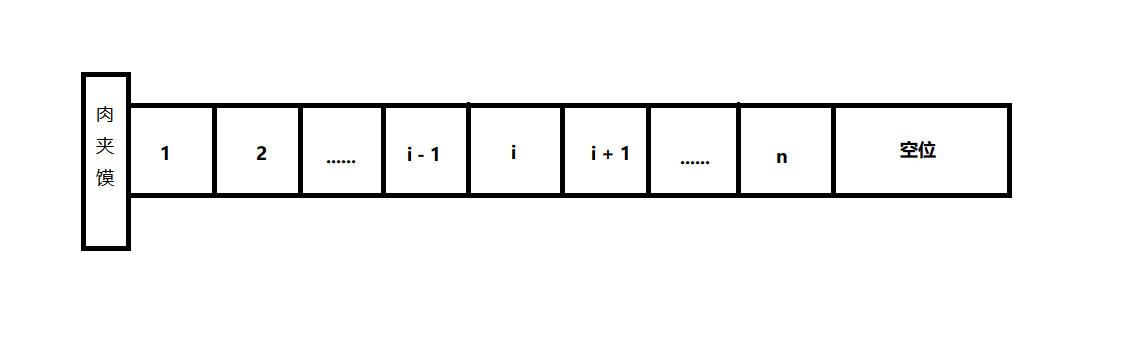
这也是顺序结构的排列方式,不能存在有人并排站的情况,这样食堂阿姨就没法给你们打饭了,因为阿姨不知道该把饭打给谁。
删除操作:排队时,有个人接了个电话,他有急事,要离开。他走了,那么剩下的人就要往前走一步,补上这个空缺。
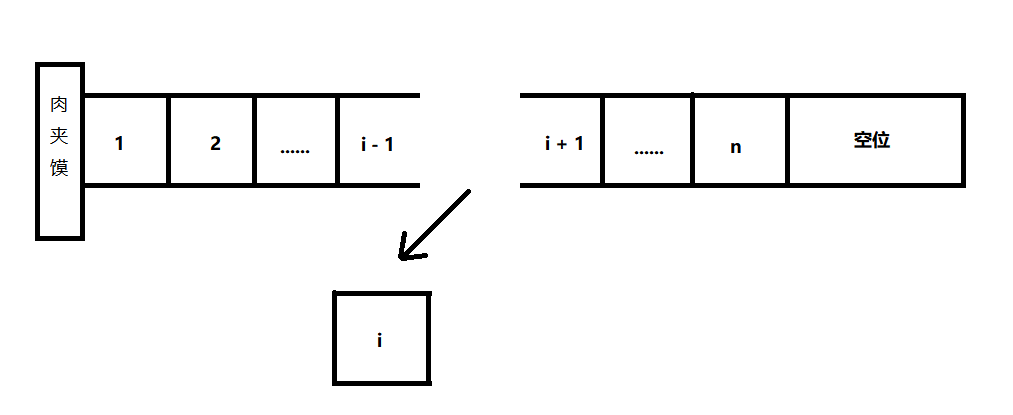
编程思路:假设那个人的位置是i,那么i + 1以及之后的人,都需要向前移动一个位置,如果那个人的位置是最后一位,则不需要有元素移动。
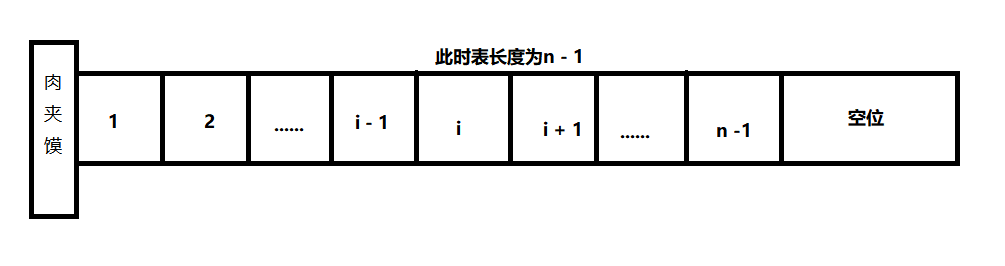
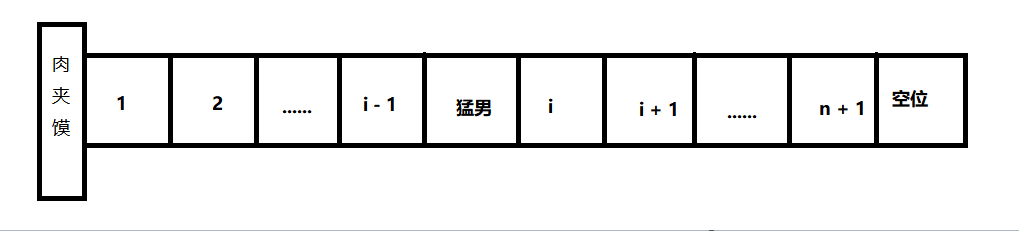
插入操作:大家都在排队,这个时候,来了一个很没有素质的长胡子猛男,他直接就插入到了队伍中的某个位置,这个时候猛男插队的位置之后的人都不敢说话,就只好给他让位置,那么这个时候大家就需要往后退一步,但是这里有一种情况,就是排队区人员满了之后,猛男也束手无策了。
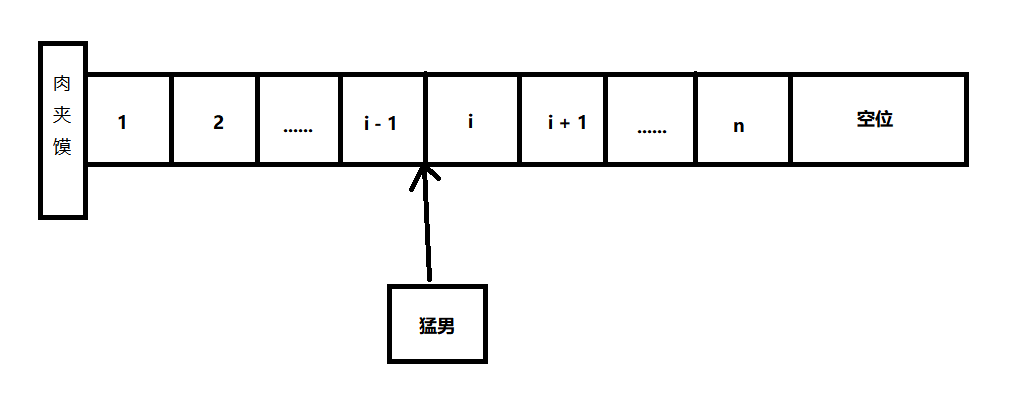
编程思路:假设那个猛男要抢占的是i的位置,那么i以及之后的元素都要向后移动,
实现-C语言
结构
我们首先需要定义一些我们会用到的数据
#define MAXSIZE 10
#define OK 1
#define ERROR 0
typedef int Status;
typedef int ElemType;
我们需要一个数据结构来模拟线性队伍
typedef struct {
ElemType data[MAXSIZE];
int length
}SqList;
插入数据
定义一个ListInsert方法,该方法有三个参数,分别是线性表,要插入的位置,以及要插入的值
Status ListInsert(SqList *L, int i, ElemType e)
{
int k;
//如果线性表元素已经满了,那么就无法再插入
if(L->length == MAXSIZE)
return ERROR;
//i不在范围内(不能将数据插入到0或比0更小的位置,i不能插入到比队伍长度还大的位置,这样就不连续了)
if(i < 1 || i > (L->length + 1))
return ERROR;
if(i <= L->length)
{
//找到最后一个元素,然后后退一个,直到将i位置的元素后退到i + 1位置时,让位操作结束
for(k = length - 1;k > i;k--)
{
L->data[k + 1] = L->data[k];
}
}
//此时空缺的位置的下标正好是i - 1,直接将元素插入即可
L->data[i - 1] = e;
//链表长度增长1
L->length++;
return OK;
}
由此我们可以得出以下结论:
- 数据插入在末尾处时,我们不需要移动任何元素,此时,时间复杂度为O(1)
- 数据插入在开始处,我们需要移动n个元素,此时,时间复杂度为O(n)
- 将数据插入到i位置,需要移动n-i+1个元素
删除数据
定义一个ListDelete方法,该方法有三个参数,分别是线性表,要删除的位置,以及取出的值
Status ListDelete(SqList *L, int i, ElemType *e)
{
if(L->length == 0)
return ERROR;
if(i < 0 || i > L->length - 1)
return ERROR;
*e = L->data[i - 1];
//i < L->length时,移除的元素不是最后一个元素
if(i < L->Length)
{
for(int k = i;k < L->length;k++)
{
L->data[k - 1] = L->data[k];
}
}
L->length--;
return OK;
}
我们可以得出以下结论
- 要删除末尾的元素时,我们不需要移动任何元素,此时,时间复杂度为O(1)
- 要删除的元素在开始处时,我们需要将n-1个元素,此时,时间复杂度是O(n)
- 删除一个位于i位置的元素,需要移动n-i个元素
获取数据
想象这么一种情况,这个时候学校的教导主任来了,然后有事情,需要从队伍中寻找一位同学,我们假设排队的位置是有编号的,如下:
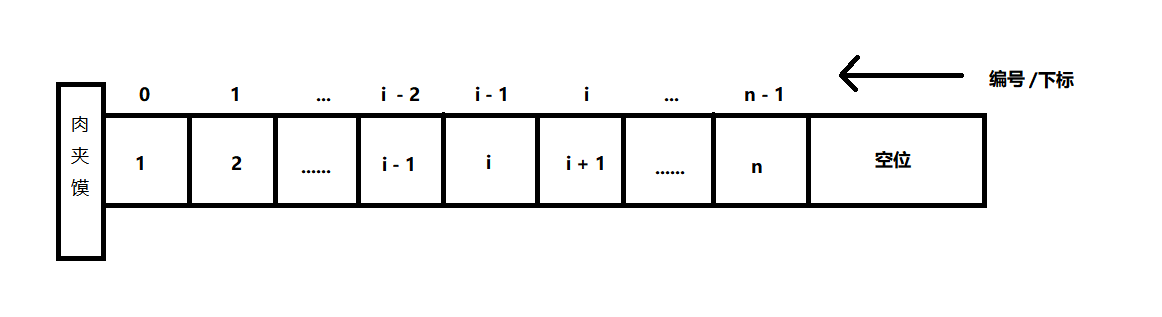
注意:下标/编号是从0开始的,那么如果队伍长度是n,那么最后一个同学的编号应该是n-1
我们使用的是数组,这正好符合我们数组的操作方式。现在教导主任说,请第i个同学出来一下,那么我们的代码应该是这个样子的:
Status GetElem(SqList *L, int i, ElemType *e)
{
if(i < 1 || L->length < i || i < 1)
return ERROR;
*e = L->data[i - 1];
return OK;
}
在获取元素时,我们不需要移动任何元素,借助数组下标的特性,我们可以对数据进行直接获取,此时,时间复杂度一直是O(1)
OK,我们可以得出以下结论了:
线性表优点
- 内存空间是固定的
- 快速获得表中任何位置的元素
线性表缺点
- 数据的插入与删除需要移动大量的删除操作
- 当线性表中的数据长度变化很大时,很难衡量该使用多长的表长度
该博客总结于书籍:大话数据结构 --很简单易懂的算法与数据结构的书


 浙公网安备 33010602011771号
浙公网安备 33010602011771号