机器学习-第一周梳理

吴恩达机器学习（一）

一、什么是机器学习(what is Machine learning)？

机器学习算法主要有两种机器学习的算法分类

1. 监督学习
2. 无监督学习

两者的区别为是否需要人工参与数据结果的标注

1.监督学习

监督学习：预先给一定数据量的输入和对应的结果即训练集，建模进行拟合，最后让计算机预测未知数据的结果。

监督学习一般有两种：

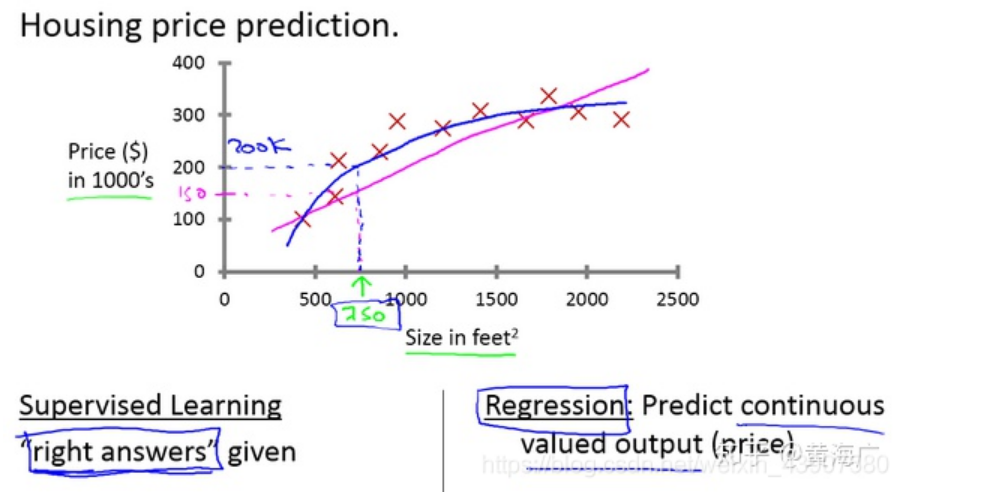
- 回归问题(Regression)

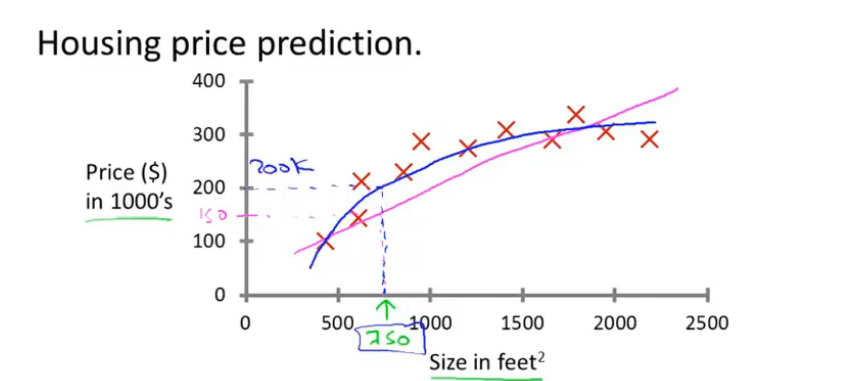
• 回归问题是预测连续值的输出，例如房价等

• 在吴恩达老师课程中，给出了一个房屋价格预测的例子中，给出了一系列的房屋面积数据，以及房屋价格，根据这些数据来搭建一个预测模型，在预测时，给出房屋面积，根据模型得出房屋价格。

- 分类问题(Classification)

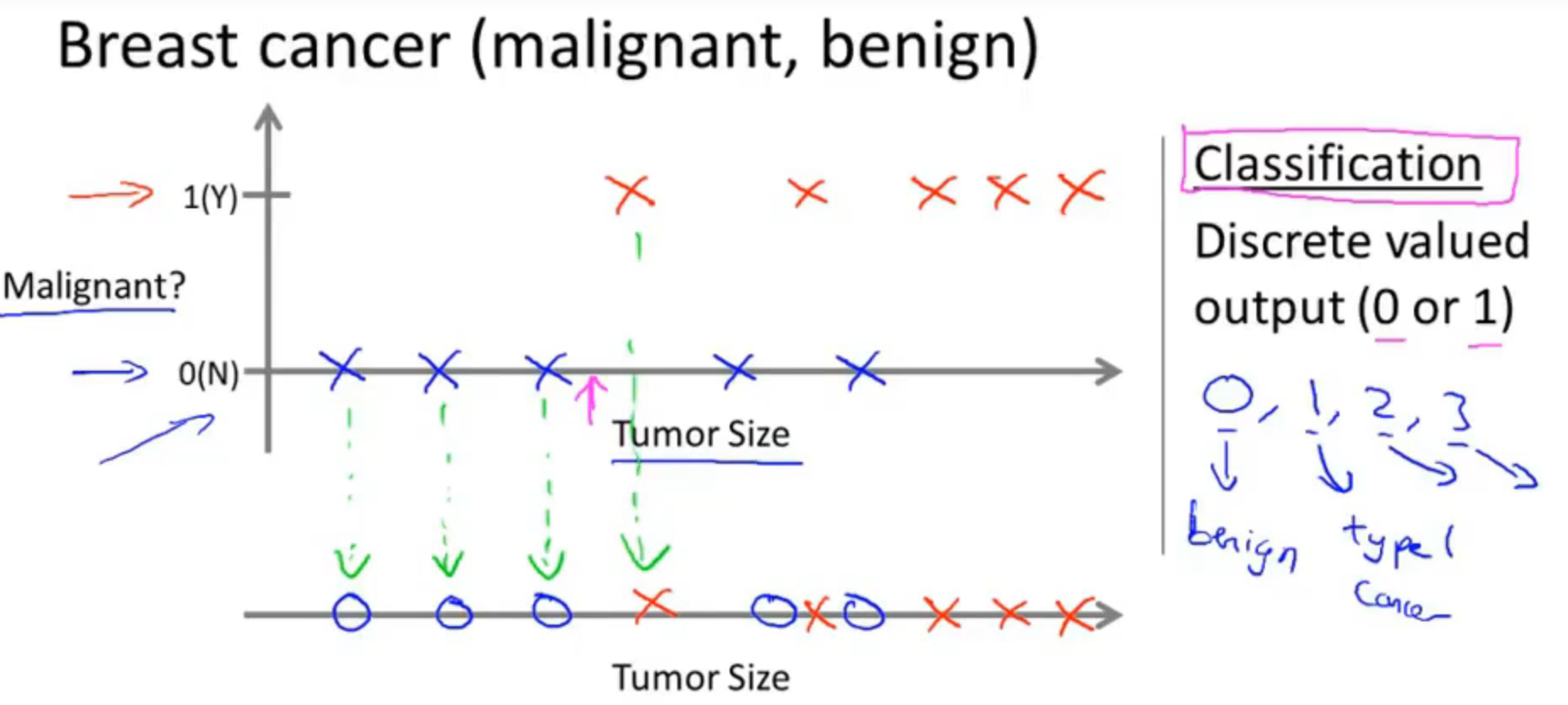
• 分类问题即为预测一系列的离散值。根据一系列数据(同回归问题不一样的是，分类问题的y值是一种离散值，比如0 or 1，又比如cat dog pig)等等，即根据数据预测被预测对象属于哪个分类。

• 在吴恩达老师课程中举了癌症肿瘤这个例子，针对诊断结果，分别分类为良性或恶性。还例如垃圾邮件分类问题，也同样属于监督学习中的分类问题。

2.无监督学习

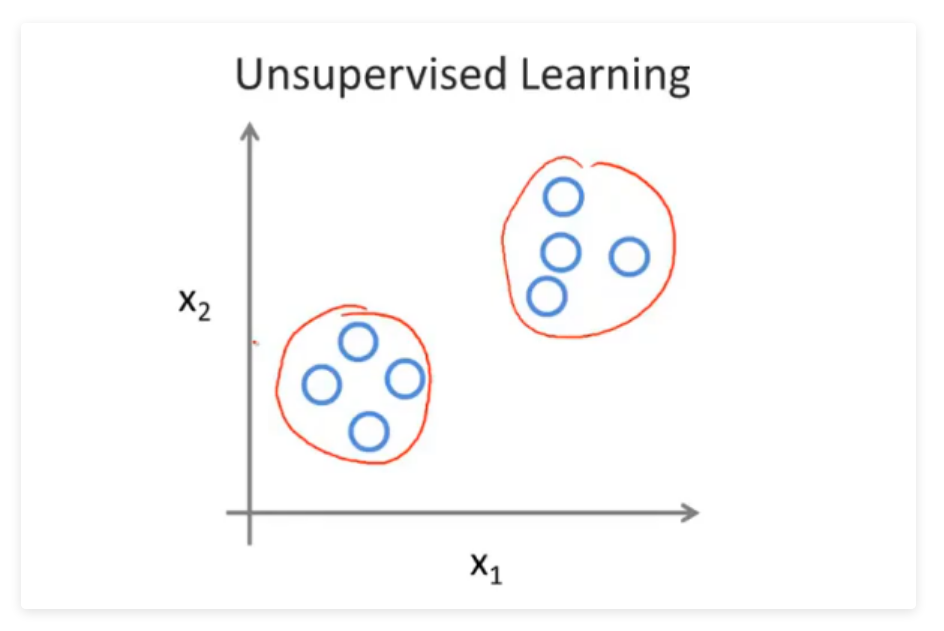
相对于监督学习，训练集不会有人为标注的结果（无反馈），无法得知训练集的结果是什么样，而是单纯由计算机通过无监督学习算法自行分析，从而“得出结果”。计算机可能会把特定的数据集归为几个不同的簇，故叫做聚类算法。

在吴恩达老师课程中，举了一个新闻的聚类问题，每天有无数条新闻，一些公司将这些新闻进行分类，将同一个话题的新闻放在一块。

二、单变量线性回归(Linear Regression with One Variable)

1.模型表示

• x 代表目标变量/输出变量
• y 代表目标变量/输出变量
• h(x) 代表假设函数
• 定义\(h ( x ) = \theta_0+\theta_1x\) 为假设函数，因此之后的任务是求出\(\theta\)，来拟合给定的数据集

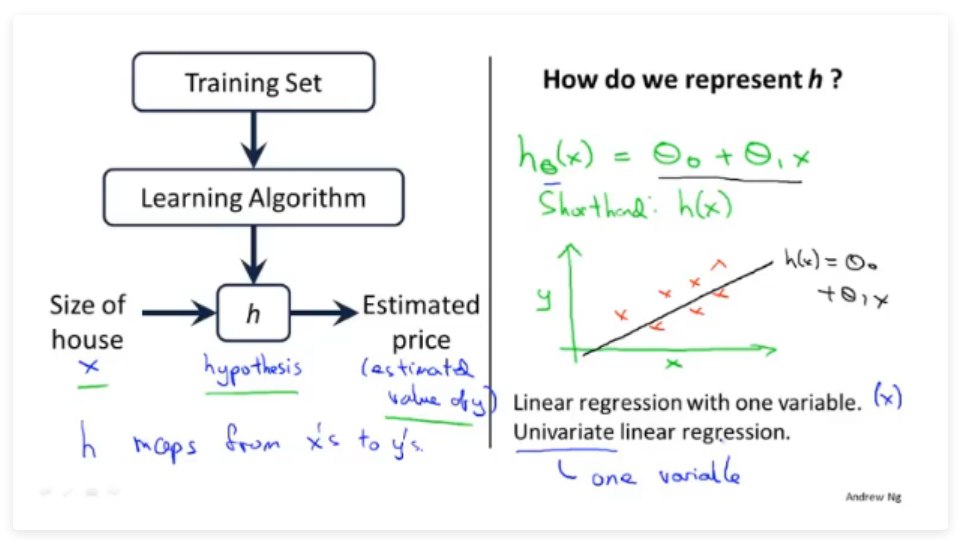
• 线性回归是拟合一条线，将训练数据尽可能分布到线上。这里我们只有一个变量x，所以成为单变量的线性回归。另外还有多变量的线性回归称为多元线性回归。

2.代价函数

2.1 定义

代价函数（cost function），一般使用最小均方差来评估参数的好坏。

定义代价函数为：\(J(θ_0,θ_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)^2\)，这里的m指的是m个已知x和y的点

2.2 可视化

• 简化假设函数\(h ( x ) = \theta_1x\)，即\(\theta_0=0\)(单参数)

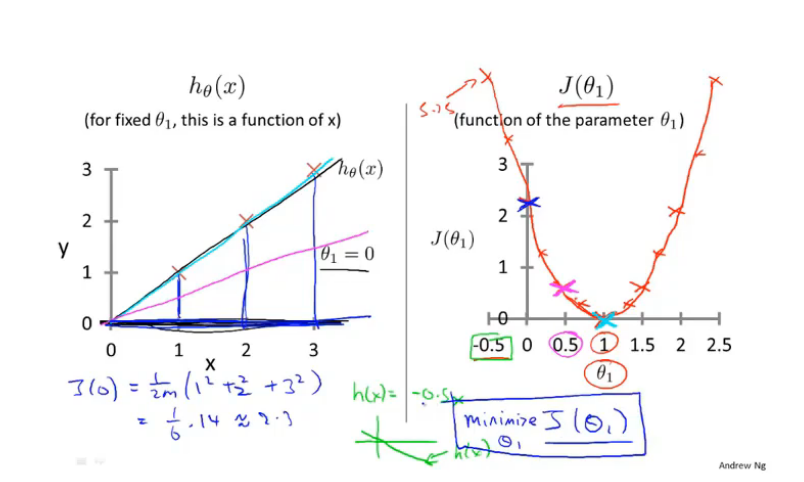
从右图中可以看到当\(\theta_1=1\)时，对应的\(J(θ_1)\)最小，而此时左图中的假设函数\(h ( x )\) 的曲线也完美拟合了我们的数据

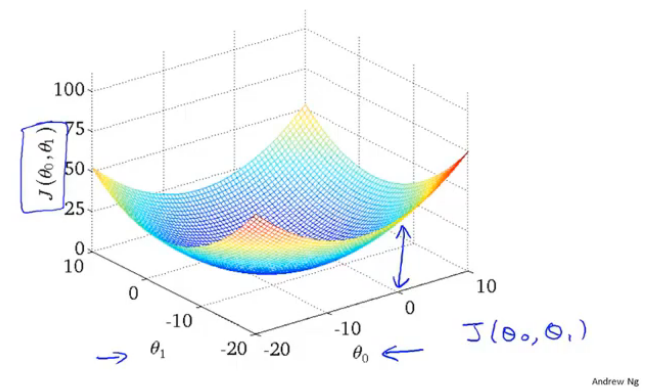
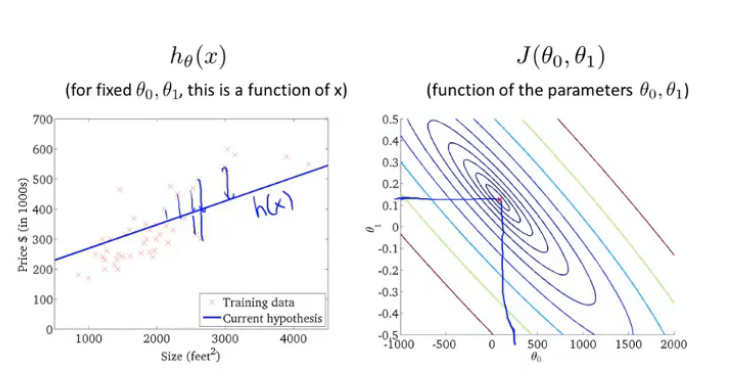
• 假设函数\(h ( x ) = \theta_0+\theta_1x\)，即双参数

此时对应的\(J(θ_1)\)为三维图形

左图为假设函数图像，右图为等高线图(三维图形投影)

总结：通过可视化我们明显地可以看到接近代价函数J最小值的点，对应着更好的假设函数和更好的数据拟合程度。

3.梯度下降

3.1 梯度

• 梯度的定义
  在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。
• 梯度的公式

以二元函数 f(x,y) 为例，分别对 x,y 求偏导，求得的梯度向量如下所示：

\[gradf(x,y)= ▽f(x,y) = \{\frac{∂f}{∂x},\frac{∂f}{∂y}\} \]

对于在点(x0,y0)的具体梯度向量就是\((\frac{∂f}{∂x0},\frac{∂f}{∂y0})\),或者▽f(x0,y0)

• 梯度的意义

几何意义：函数变化增加最快的地方。具体来说，对于函数f(x,y),在点(x0,y0)，沿着梯度向量的方向就是\((\frac{∂f}{∂x0},\frac{∂f}{∂y0})\)的方向是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是\(-(\frac{∂f}{∂x0},\frac{∂f}{∂y0})\)的方向，梯度减少最快，也就是更加容易找到函数的最小值

3.2 梯度下降思想

• 开始时，我们随机选择一个参数组合即起始点，计算代价函数，然后寻找下一个能使得代价函数下降最多的参数组合。不断迭代，直到找到一个局部最小值(local minimum)，由于下降的情况只考虑当前参数组合周围的情况，所以无法确定当前的局部最小值是否就是全局最小值(global minimum)，不同的初始参数组合，可能会产生不同的局部最小值。

3.3 梯度下降的具体执行

• 梯度下降的公式：\(θj=θj−α\frac{∂}{∂θ_j}(J(θ0,θ1,⋯,θn))\)

注意：梯度下降在具体的执行时，每一次更新需要同时更新所有的参数。

• 梯度下降公式中有两个部分：学习率和偏导数

偏导数这部分决定了下降的方向即”下一步往哪里“走

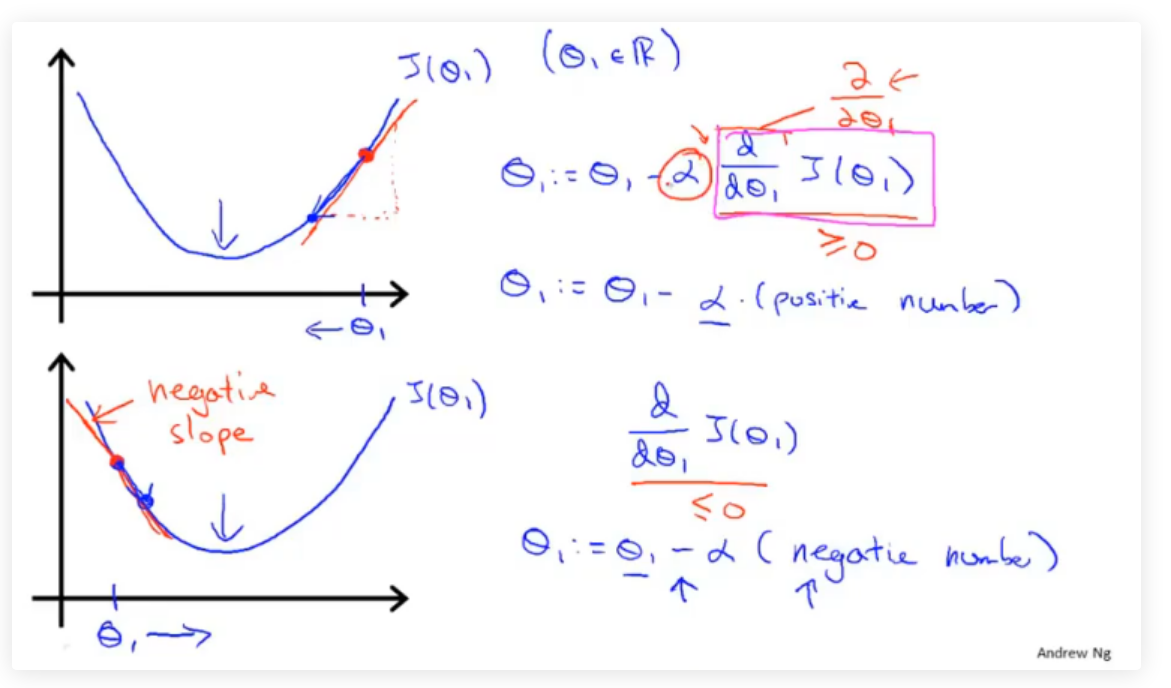
下图举一个代价函数\(J(\theta_1)\)例子，其中偏导数用来计算当前参数对应代价函数的斜率，导数为正则\(θ\)减小，导数为负则\(θ\)增大，通过这样的方式可以使整体向\(\frac{∂}{∂θ_1}J(θ1)=0\)收敛

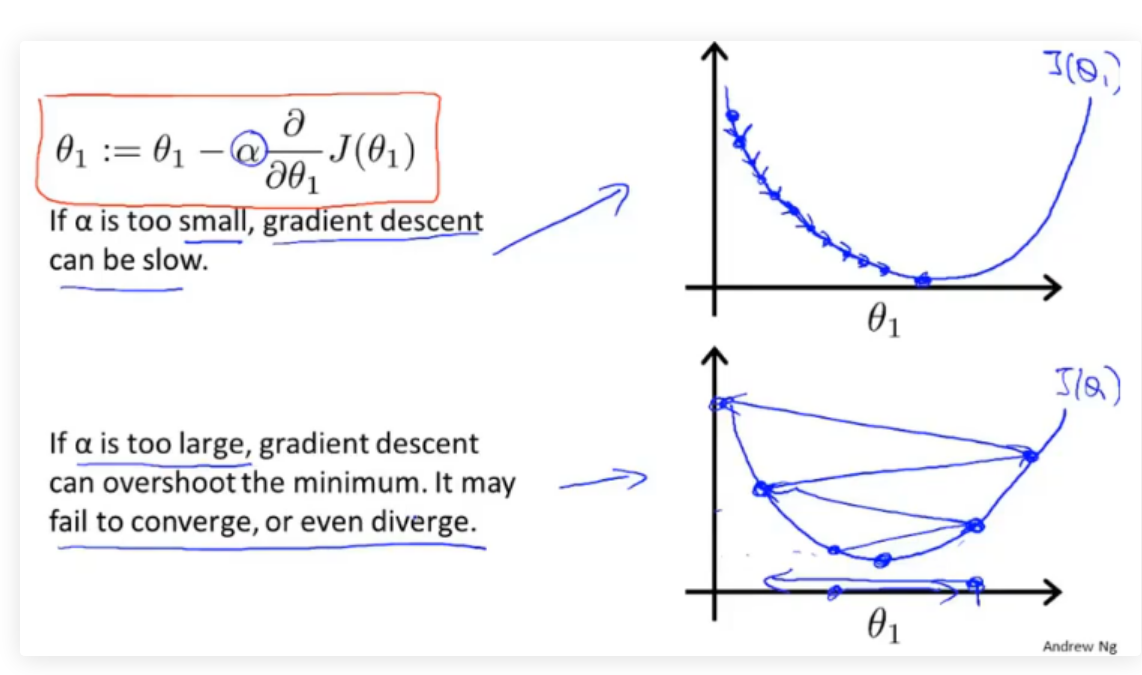
公式中，学习速率\(α\)决定了参数值变化的速率即”走多少距离“，

\(α\)用来描述学习率，即每次参数更新的步长。如下图所示，\(α\)的大小不好确定，如果太小则需要很多步才能收敛，如果太大最后可能不会收敛甚至可能发散。

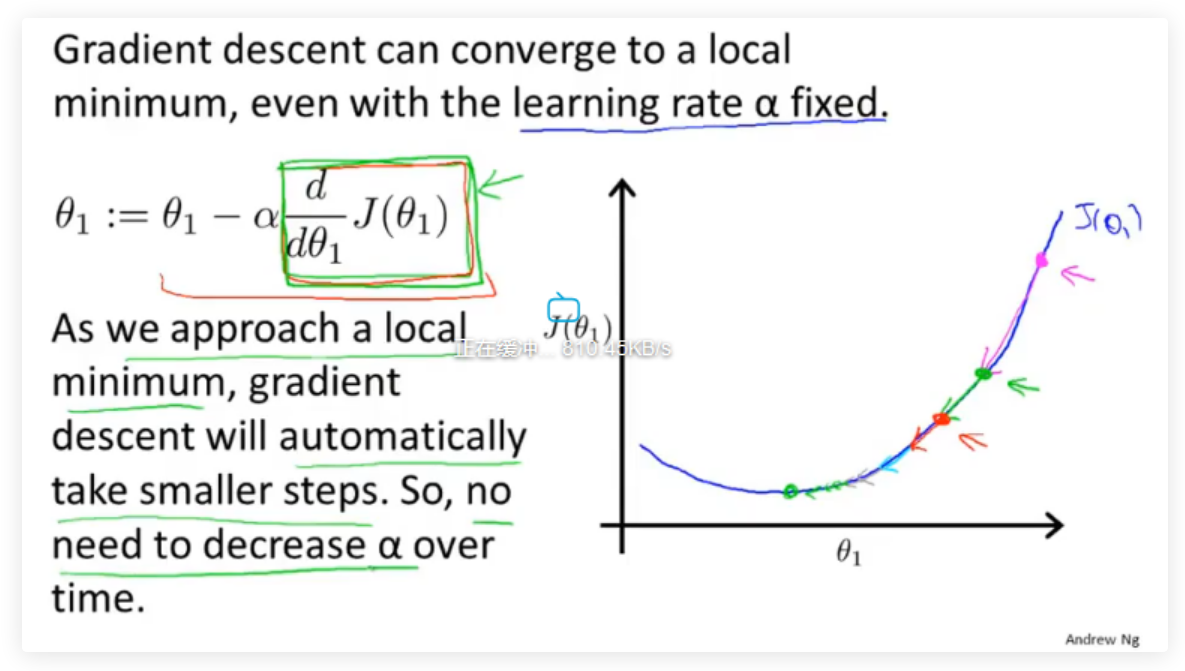
当\(θ\)处于局部最优解时，\(θ\)的值将不再更新，因为偏导为0。

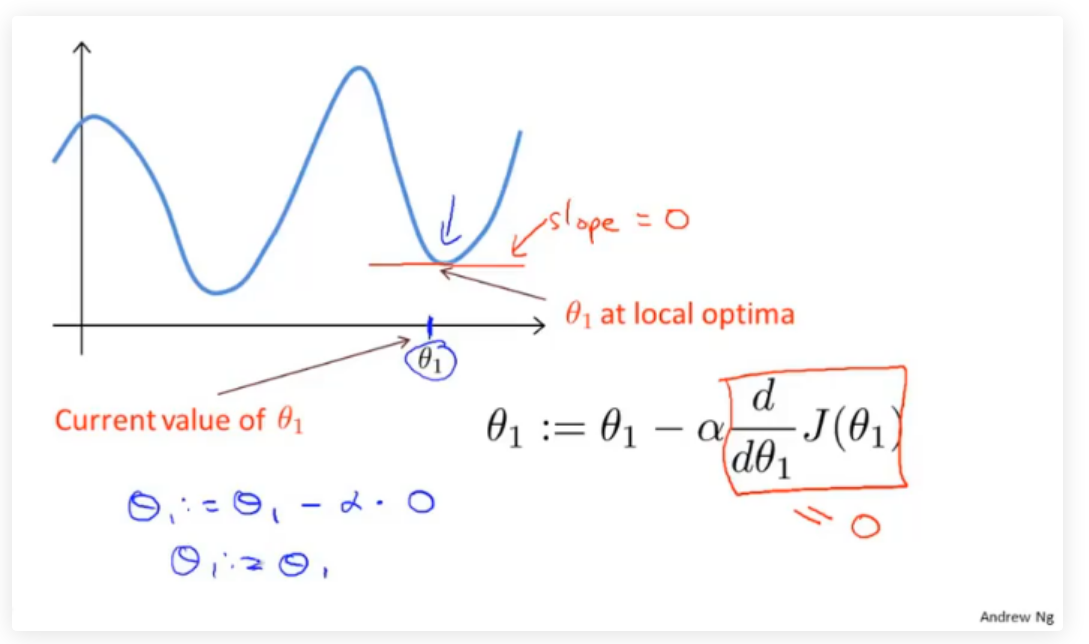
这也说明了如果学习率\(α\)不改变，参数也可能收敛，假设偏导>0，因为偏导一直在向在减小，所以每次的步长也会慢慢减小，所以\(α\)不需要额外的减小。

3.4 单元梯度下降

梯度下降每次更新的都需要进行偏导计算，这个偏导对应线性回归的代价函数。

将线性回归的代价函数带入，并求导的结果为：

\[\frac{∂}{∂θ_j}J(θ_0,θ_1) =\frac{∂}{∂θ_j}\frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)^2\\ =\frac{∂}{∂θ_j}\frac{1}{2m}\sum_{i=1}^{m}( \theta_0+\theta_1x^i-y^i)^2 \\ θ_0(j=0):\frac{∂}{∂θ_0}J(θ_0,θ_1)= \frac{1}{m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)\\ θ_1(j=1):\frac{∂}{∂θ_1}J(θ_0,θ_1)= \frac{1}{m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)*x^i \]

梯度下降的过程容易出现局部最优解：

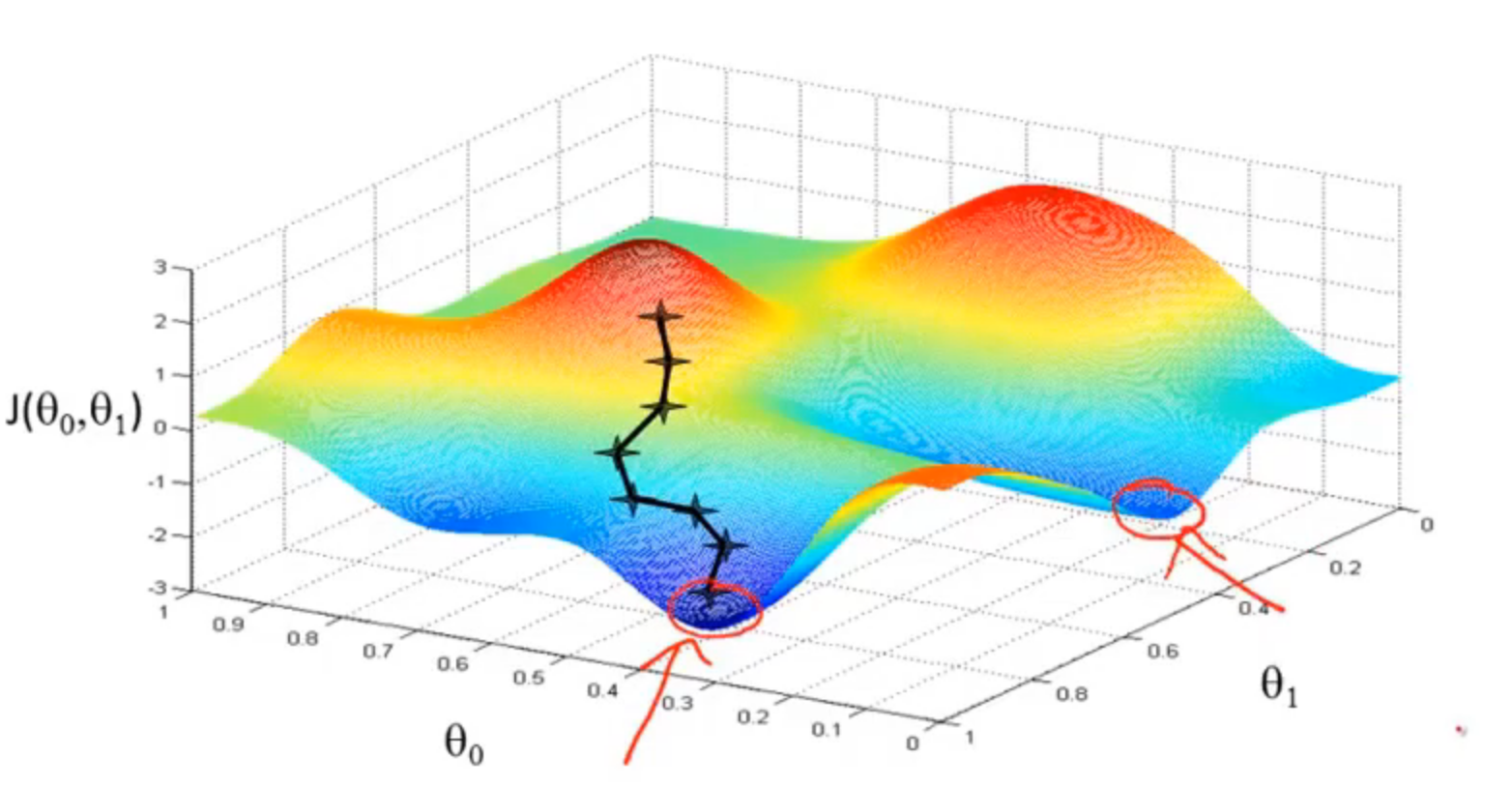
但是线性回归的代价函数，往往是一个凸函数。它总能收敛到全局最优。

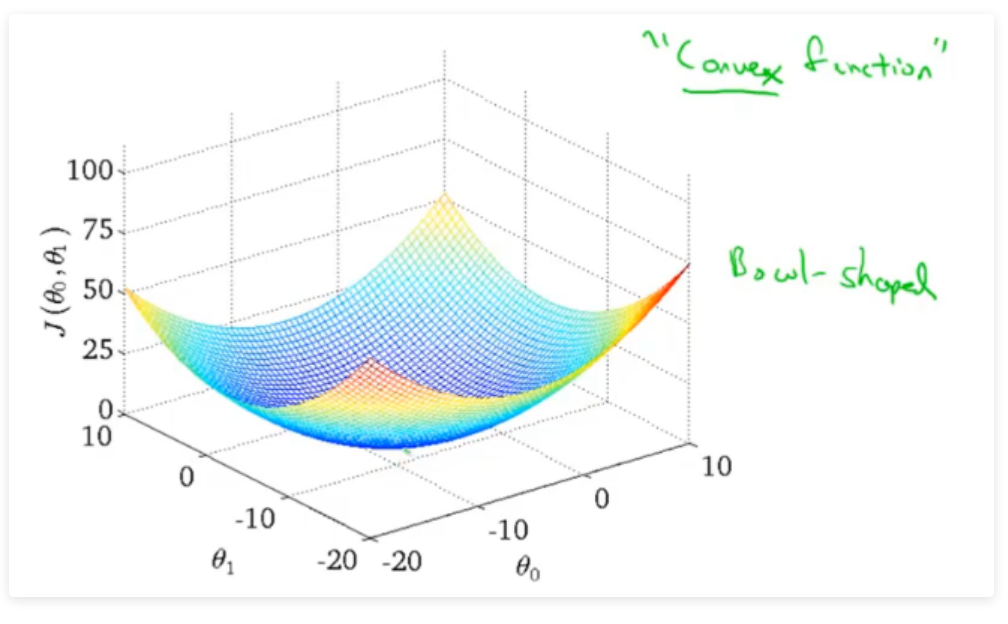
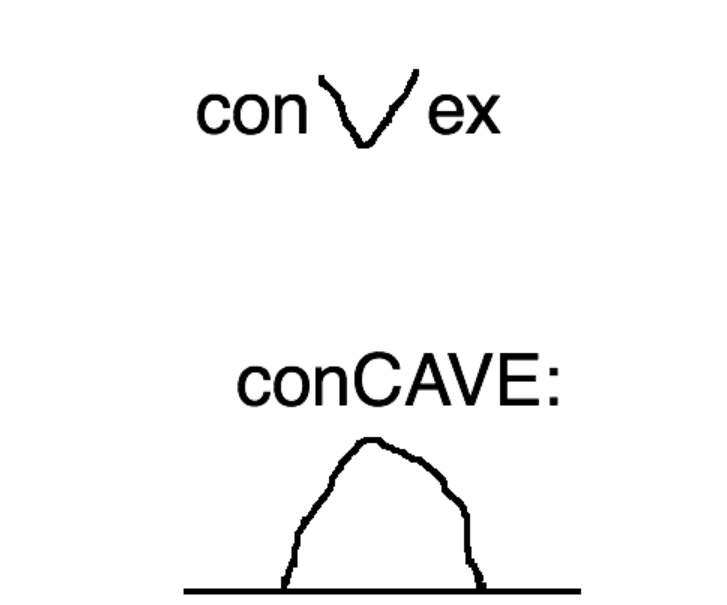
关于凸函数与凹函数，国内外是刚好相反的，其实说哪边是凸哪边是凹都有一定道理。

我曾在知乎看到外国人可能是这样记的-☺

梯度下降过程的动图展示：

上述梯度下降的方法也被称为“Batch”梯度下降：在每一步梯度下降，我们都遍历了整个训练集的样本

三、多变量线性回归

1.模型表示

比如之前的房屋价格预测例子中，除了房屋的面积大小，可能还有房屋的年限、房屋的层数等等其他特征：

在这次模型中设假设函数为\(h_\theta( x ) = \theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\theta_4x_4\)

运用线性代数可简化为:

\[h_\theta( x ) = \left[ \matrix{ \theta_0 \ \theta_1 \ \theta_2 \ \theta_3 \ \theta_4 \ } \right] \left[ \matrix{ x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ } \right] = \theta^Tx \]

2 、多变量梯度下降(Gradient Descent for Multiple Variables)

• 第一步：写出代价函数

\[J(θ_0,θ_1...\theta_n) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)^2 \]

• 第二步：写出梯度下降公式

\[θj=θj−α\frac{∂}{∂θ_j}(J(θ0,θ1,⋯,θn)) \]

• 第三步：求出偏导数，带入梯度下降公式

\[θj=θj−α\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)x_j^i \]

\(x_j^i\)表示第i个数据样本中的第j个特征

3.特征缩放

等高线中的梯度

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

PS1：为什么会导致等高线图出现比较扁的情况？
由于x1的尺度比较大(0_{2000)，而x2的尺度小(0}5)，因此\(\theta_1\)对y的影响大很多

PS2：为什么左图中梯度上升过程中来回震荡，呈现锯齿状上升？

由于梯度与等高线的切线方向垂直，椭圆越扁垂线可能就越容易接近水平，自然就更不容易向上。

具体的证明请看：直观理解梯度，以及偏导数、方向导数和法向量等 - shine-lee - 博客园 (cnblogs.com)

为了优化梯度下降的收敛速度，采用特征缩放的技巧，使各特征值的范围尽量一致，让\(x_i\)保持在一个比较小的范围内。这样在进行梯度下降收敛的时候速度会比较快。

常用的特征缩放的方法

(1) 标准化

标准化将值替换为z-score。这个重新分布的特征意味着μ= 0和标准偏差σ= 1

\[x' = \frac{x-\bar x}{\sigma} \]

(2) 均值归一化:

\[x’ = \frac{x-mean(x)}{max(x)-min(x)} \]

这个分布的值域为[-1,1]，μ=0。

标准化和均值归一化可用于假设中心数据为零的算法，如主成分分析(PCA).

(3) 最小-最大值缩放:

\[x' = \frac{x-min(x)}{max(x)-min(x)} \]

这种缩放使值介于0和1之间。

(4) 单位向量化:

\[x'= \frac{x}{\|x\|} \]

这个缩放考虑到将整个特征向量归一化到单位长度。

最小-最大缩放和单位向量化技术产生的值范围为[0,1]。当处理带有硬边界的特征时，这非常有用。例如，在处理图像数据时，颜色的范围只能从0到255。

4.学习速率

α的选择不能过大，也不能过小，如果过大代价函数无法收敛，如果过小，代价函数收敛的太慢。当然， 足够小时，代价函数在每轮迭代后一定会减少。可以通过在收敛的过程中绘制图像，来直观的感受α的选值，一开始我们可以选择0.001 , 0.003 , 0.01 , 0.03 等等。

5.多项式回归

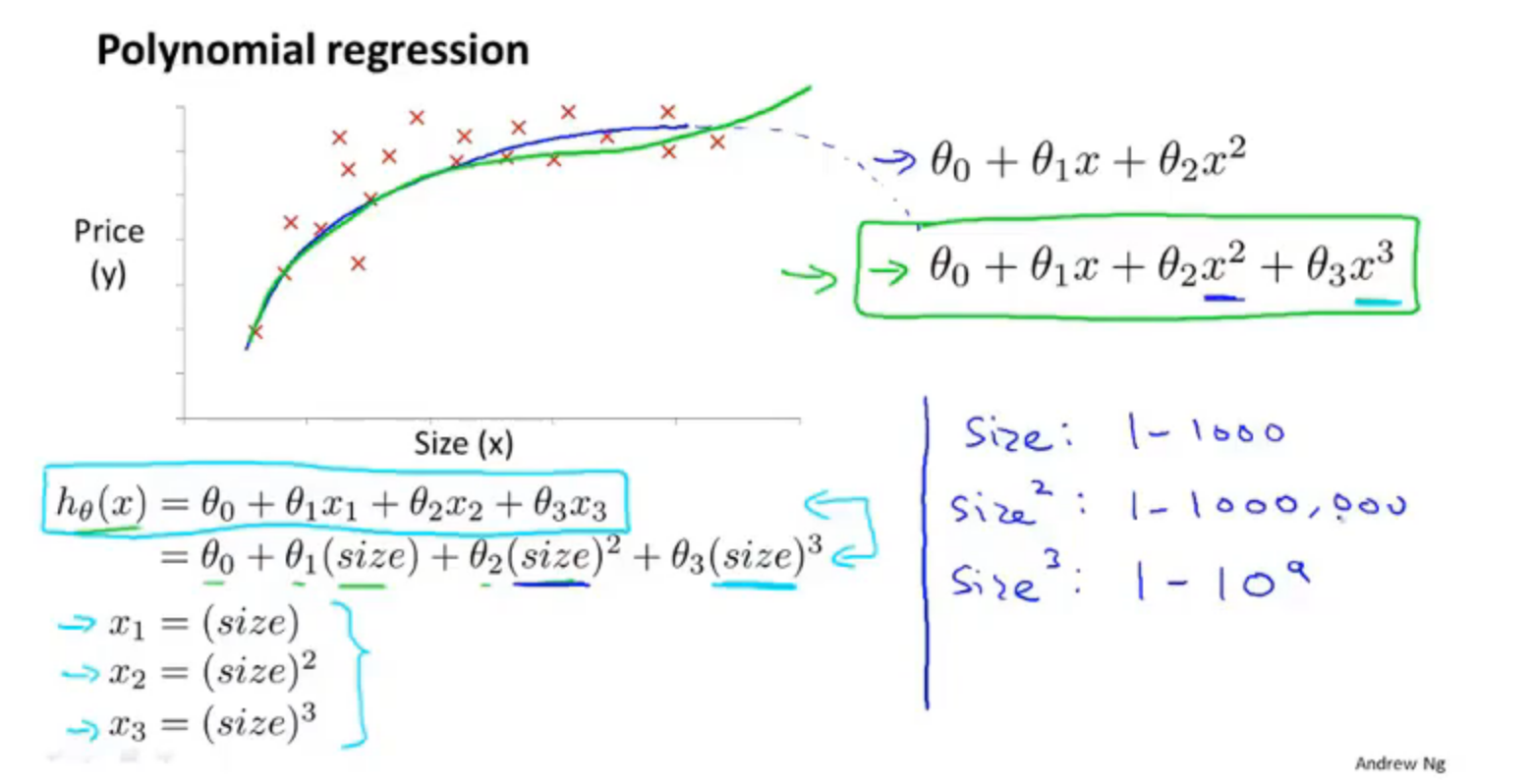
线性回归只能以直线来对数据进行拟合，有时候需要使用曲线来对数据进行拟合，即多项式回归(Polynomial Regression)。比如定义一个假设函数

\[h_\theta( x ) = \theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3 \]

在这里可能有人会有疑问，上述假设函数都涉及到3次方了，怎么还是线性回归，在这里线性回归中的线性的含义：因变量y对于未知的回归参数θ是线性的，注意区分线性回归方程和线性函数，如果方程中包含自变量的N次项，则可以将自变量作为一个整体来考虑

在使用多项式回归时，非常有必要进行特征缩放，比如\(x_1\)的范围为 1 − 1000，那么\(x_1^2\)的范围则为 1 −1000000

6.正规方程

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：

\[\frac{∂}{∂θ_j}J(θ_j) = 0 \]

假设我们的训练集特征矩阵为X并且我们的训练集结果为向量y, 则利用正规方程解出向量\(\theta = (X^TX)^{-1}X^Ty\)

正规方程的思想和高数中使用偏导数为0求解最值（极值）一样

正规方程的推导过程

到底梯度下降和正规方程如何选择，可以参考一下表格

梯度下降	正规方程
需要选择学习率\(\alpha\)	不需要学习率
需要多次迭代	一次运算即可得出
当特征量n大时也能较好的适用	需要计算\((X^TX)^{-1}\)，如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为\(O(n^3)\)，通常来说当n小于10000时还是可以接受的
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其他模型