机器学习-第二周梳理

吴恩达机器学习（二）

二分类逻辑回归

1.分类问题

逻辑回归算法是分类算法，我们将它作为分类算法使用。它适用于标签 𝑦 取值离散的情况，如:1 0。

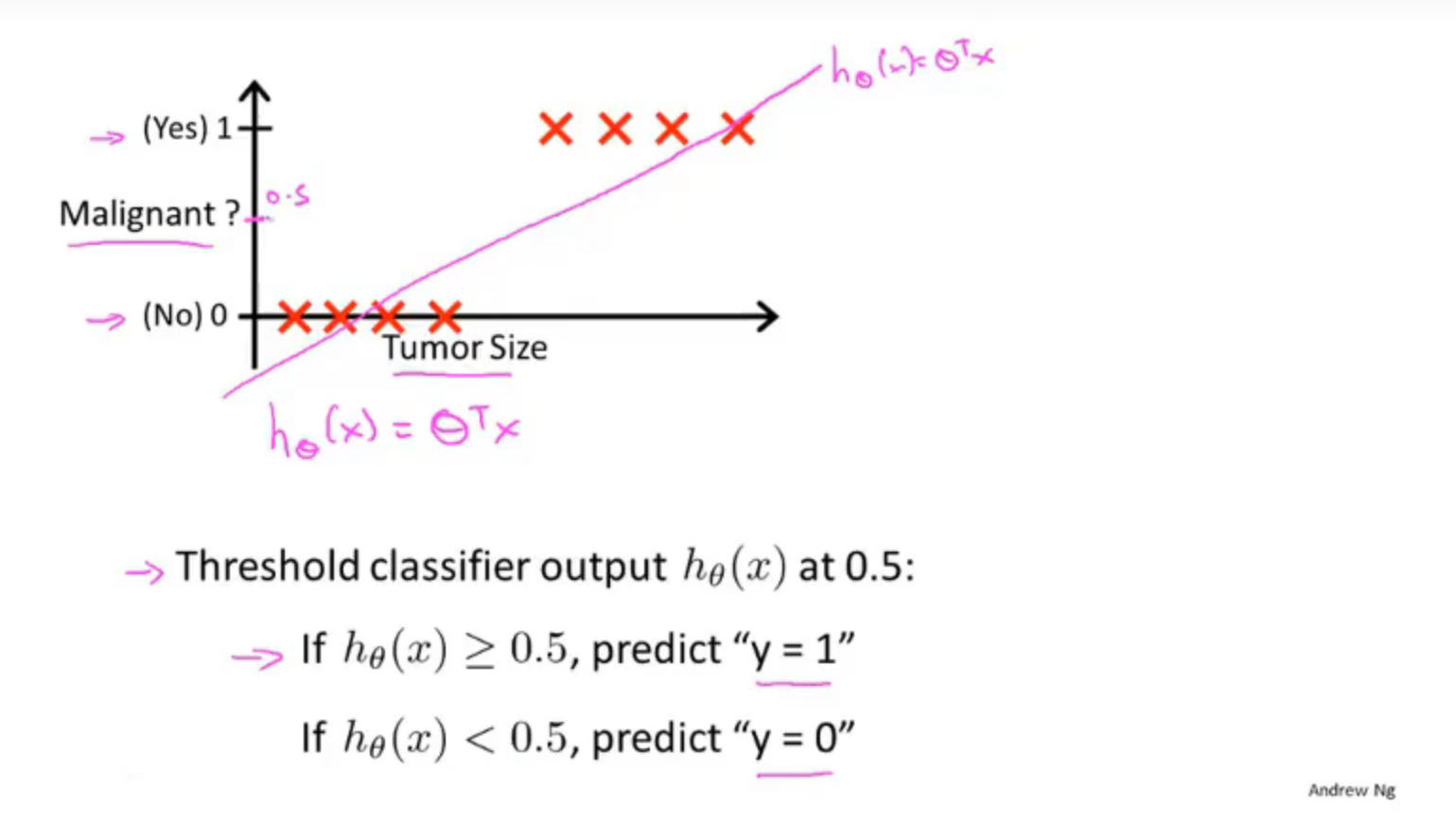
在吴恩达机器学习中举了一个肿瘤诊断问题，输出值y ∈ { 0 , 1 } ，0表示良性肿瘤，1表示恶性肿瘤

首先我们会想到将学到的线性回归的方法作用于分类问题，通过设置分类器输出的阈值来对输入值进行分类，但这种方法有时效果好，有时效果很差，并不推荐，

2.假设函数的表示

在逻辑回归中用Sigmoid函数实现区间0~1之间的的输出，Sigmoid函数

\[g(z) = \frac{1}{1+e^{-z}} \]

函数图像如下所示

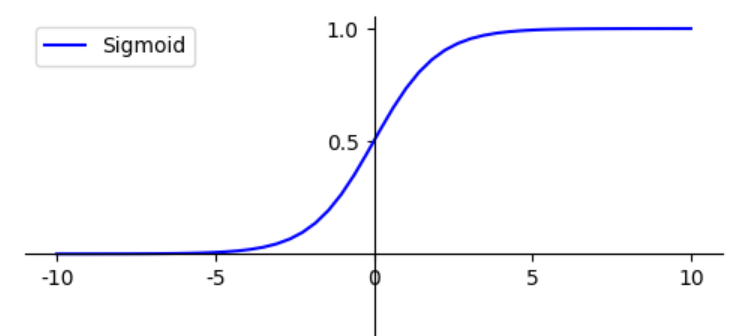
设假设函数为：

\[h_\theta(x) = g(\theta^Tx) = \frac{1}{1+e^{-\theta^Tx}} \]

因此我们用以下假设对预测进行分类：

\(h_\theta \geq 0.5\)，则预测 y = 1

\(h_\theta < 0.5\) ，则预测 y = 0

3.决策边界

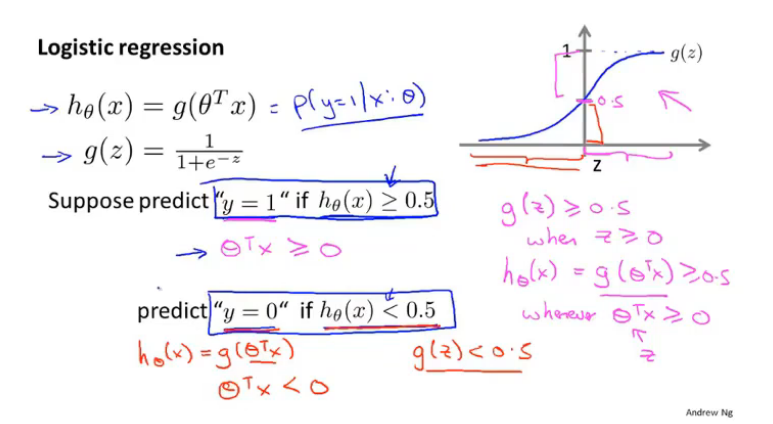
根据假设函数的图像我们可以得出：

\[y=1:h_\theta(x) = g(\theta^Tx) \geq 0.5 \longrightarrow \theta^Tx \geq 0 \\ y=0:h_\theta(x) = g(\theta^Tx) < 0.5 \longrightarrow \theta^Tx < 0 \]

假设有一个模型，我们已经拟合好了参数\(\theta\)

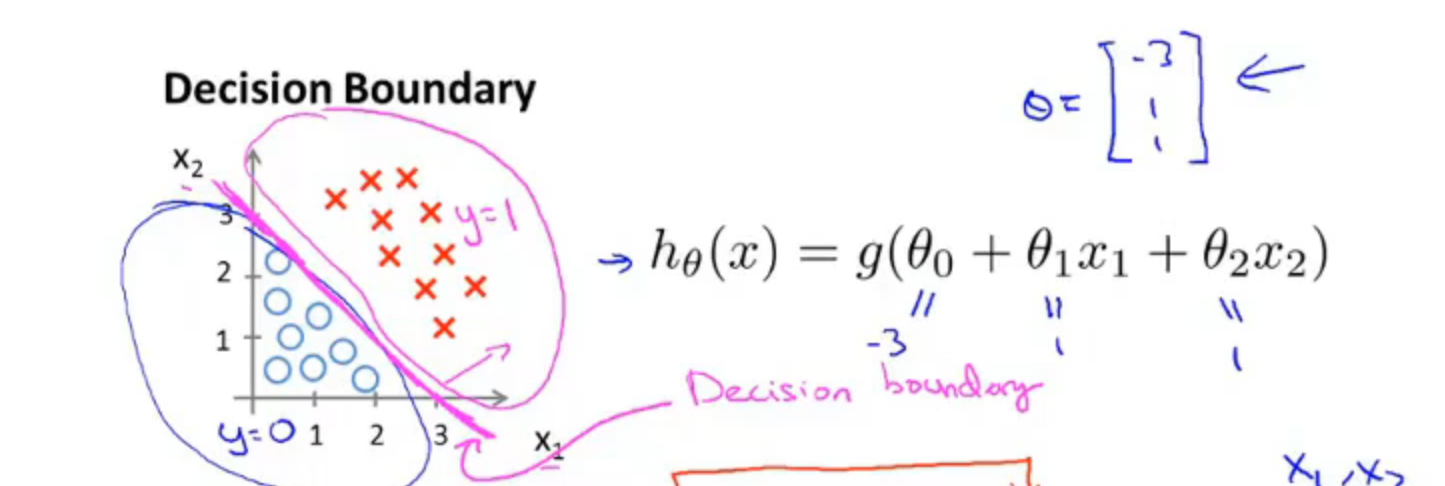
并且参数𝜃 是向量[-3 1 1]。 则当\(-1+x2+x3 \geq 0\)，即\(x2 + x3 \geq 3\)时，模型将预测 𝑦 = 1。 我们可以绘制直线：\(x2+x3=3\)，这条线便是我们模型的分界线，将预测为 1 的区域和预测为 0 的区域分隔开。

这条线即被称为—决策边界，决策边界将平面分成两个区域，一个区域假设函数预测y=1，而另一个区域预测y=0。决策边界是假设函数的属性而不是数据集的属性，它取决于假设函数的参数

4.损失函数

在之前一节中的线性回归中，用到损失函数是平方差的形式，但是对于逻辑回归来说，平方差的形式的损失函数时不行的，因为假设函数\(h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}\)是一个非线性函数，若仍按照以下损失函数

\[J(θ) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)^2 \]

则\(J(\theta)\)的图像如下

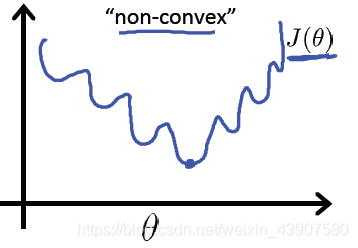
可以看到是一个非凸函数，有许多局部最小点，在我们之后进行梯度下降优化参数的时候，无法收敛到全局最优点。

因此定义逻辑回归损失函数：

\[J(\theta) = \frac{1}{m}\sum_{i=1}^{m}Cost(h_θ(x^i),y^i) \]

其中：

\[Cost(h_θ(x),y) = \begin{cases} -log(h_\theta(x)), & \text{if }y\text{ = 1} \\ -log(1-h_\theta(x)), & \text{if }y\text{ = 0} \end{cases} \]

对损失函数公式进行简单的解释：

首先假设y = 1时，假设函数\(h_\theta(x)\)预测值为1，那么代价值就为0，因为预测的很正确。

相反，如果假设函数\(h_\theta(x)\)预测值趋近于0，但是实际y=1，那么我们就必须用一个非常大的代价值来惩罚这个学习算法，即代价值就趋近于无穷

同理下图 y = 0 时也是这个道理

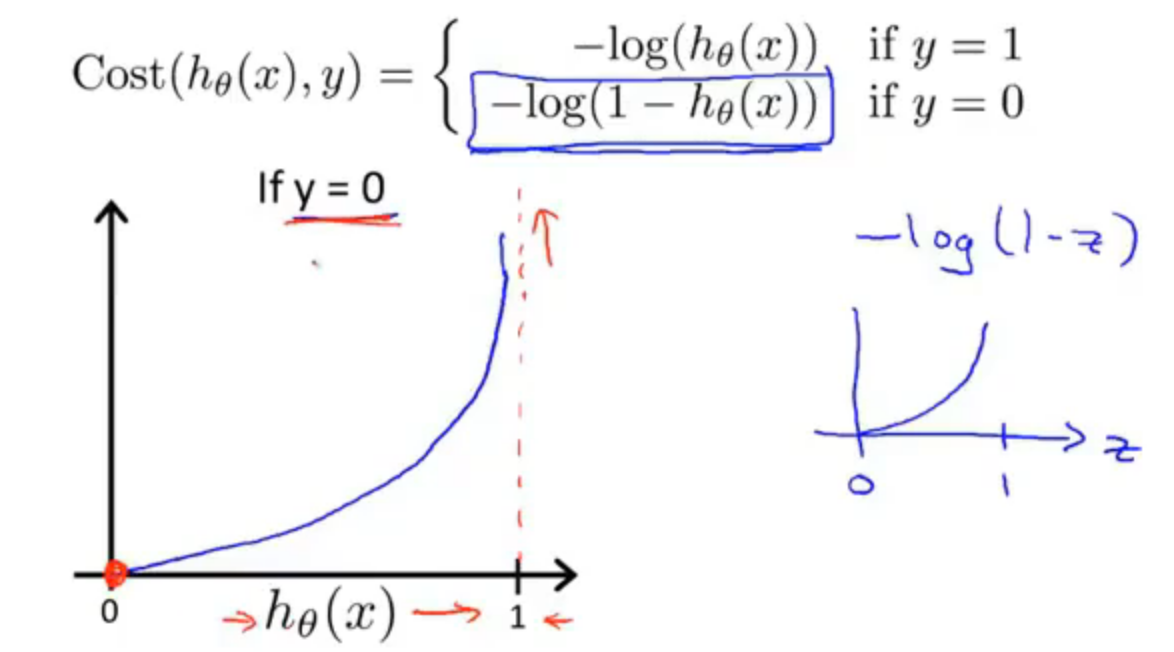
最后，我们对上面的代价函数进行优化合并：

\[Cost(h_θ(x),y) = -ylog(h_\theta(x))-(1-y)log(1-h_\theta(x)) \]

\[J(\theta)= \frac{1}{m}\sum_{i=1}^{m}[-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \]

现在代价函数已经写出来了，那么现在需要做的是最小化代价函数，我们可以使用梯度下降算法来求使得代价函数最小化的参数：

在运行梯度下降算法是，对特征进行缩放也是非常有必要的。

5.进阶优化

我们编写代码给出代价函数及其偏导数然后传入梯度下降算法中，接下来算法则会为我们最小化代价函数给出参数的最优解。这类算法被称为最优化算法，梯度下降算法不是唯一的最小化算法
一些最优化算法：

• 梯度下降法(Gradient Descent)
• 共轭梯度算法(Conjugate gradient)
• 牛顿法和拟牛顿法(Newton’s method & Quasi-Newton Methods)（DFP算法，
  局部优化法(BFGS)，
  有限内存局部优化法(L-BFGS)）

在使用python实现最优化算法是，scipy对这类算法进行封装，直接调用即可

6.一对多分类

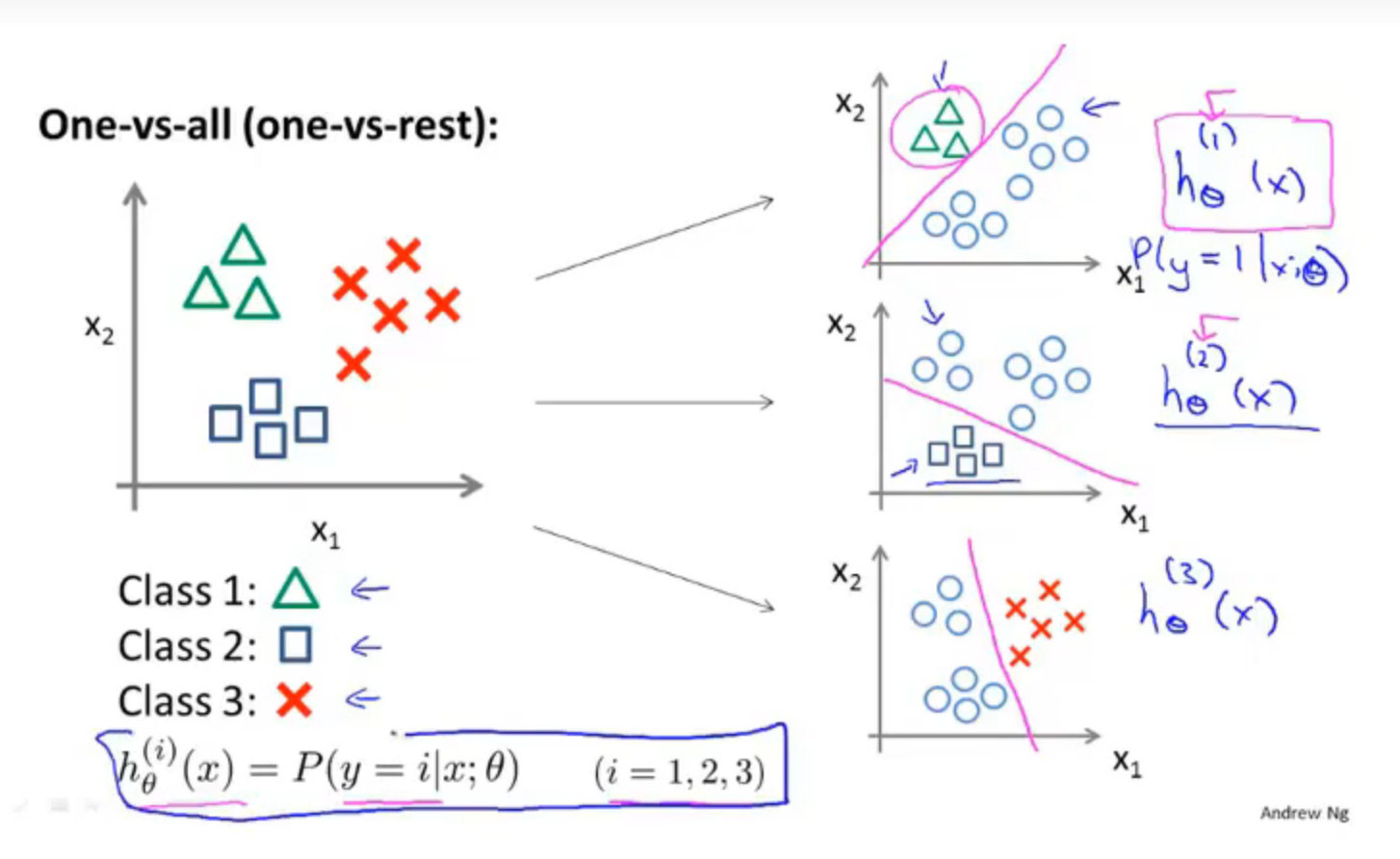
一对多分类其实就相当于进行多次二元分类，假如如上图的多元分类一样，一共有三个类别需要分类，那么本质上就是进行3次二元分类，第一轮我只关注绿色三角，将绿三角标记为正向类 y = 1、将红叉叉和蓝框框都标记为负向类；经过这一轮。我就可以判断出一个数据是绿三角的概率了；然后再对红叉叉建立模型，将红叉叉标记为正相类 y = 2,绿三角和蓝框框都标为负向类，最后对蓝框框做同样的操作。

总结：对于一对多分类，我们要训练多个二元分类器，最后我们根据输入x预测y值时，要选出可信度最高、效果最好的分类器，也就是概率值最高的。

正则化

1.拟合函数

对于拟合问题可以分为3种情况：

• 欠拟合：无法很好的拟合训练集中的数据，预测值和实际值的误差很大。即偏差大（预测值和标签偏离较大），如下图左一。
• 过拟合：能很好甚至完美拟合训练集中的数据，但是泛化能力差，$J(\theta) \longrightarrow 0 $,即方差过大（不同的数据集有比较大的波动），下图右一。
• 优良的拟合：如字样，模型预测的比较好。下图中间。

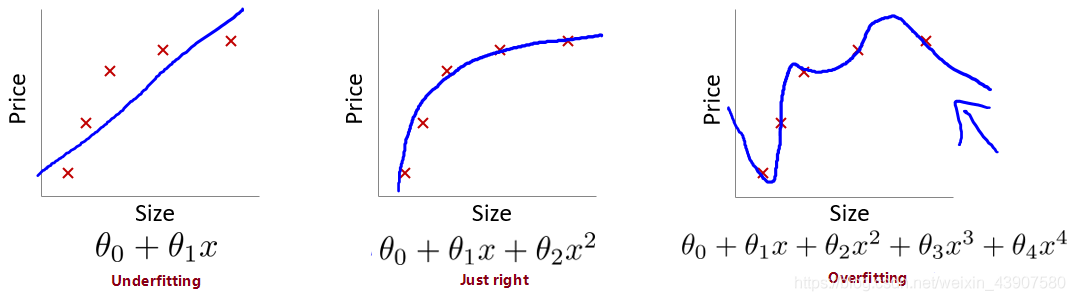
避免过拟合的方法：

• 减少特征的数量
  - 选取合适的特征（PCA）
• 正则化
  - 惩罚各参数大小

2.正则化的代价函数

原理：在损失函数上加上某些规则（限制），缩小解空间，从而减少求出过拟合解的可能性

在目标函数后面添加一个系数的“惩罚项”是正则化的常用方式，为了防止系数过大从而让模型变得复杂。在加了正则化项之后的目标函数为:

\[J(θ) = \frac{1}{m}\{\sum_{i=1}^{m}(h_θ(x^i)−y^i)^2+\lambda\sum_{j=1}^{m}\theta_j^2\} \]

其中\(\lambda\) 是一个超参数，用于控制正则化程度

3.线性回归的正则化

线性回归求解有两种算法：一种是梯度下降，另一种是正规方程

（一）梯度下降

加上正则项后的代价函数如下所示：

梯度下降的过程：

\[θj=θj−α[\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)x_j^i + \frac{\lambda}{m}\theta_j] \]

将式子进行合并可得：

\[θj=θj(1-\alpha\frac{\lambda}{m})−α\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)x_j^i \]

其中\(1-\alpha\frac{\lambda}{m} < 1\)，一般是比1略小的数

（二）正规方程

\[\theta = (X^TX+\left[ \begin{matrix} 0 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{matrix} \right])^{-1}X^Ty \]

4.逻辑回归的正则化

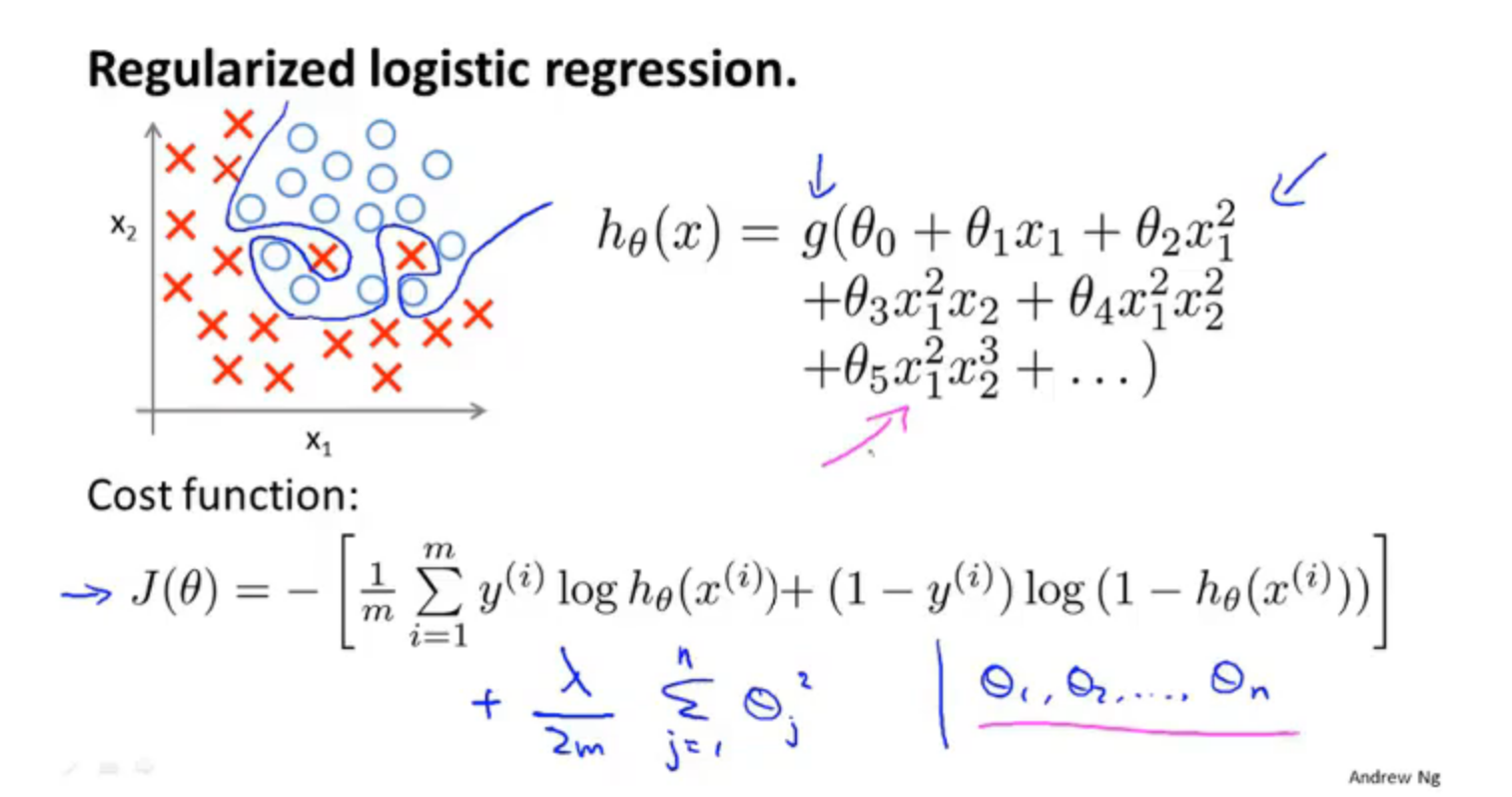
加上正则项后的代价函数如下所示：

\[J(\theta) = -[\frac{1}{m}\sum_{i=1}^{m}y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^{m}\theta_j^2 \]

效果是当拟合阶数很高且参数很多时，只要添加了这个正则项，保持参数较小，就能得到一条很好的划分边界，防止过拟合。

梯度下降过程

注意这里公式跟线性回归是相同的，但是假设函数是不同的，逻辑回归是激活函数

\[θj=θj−α\frac{∂}{∂θ_j}J(θ) \\ =θj−α[\frac{1}{m}\sum_{i=1}^{m}(h_θ(x^i)−y^i)x_j^i + \frac{\lambda}{m}\theta_j] \]