题目：斐波那契数列，又称黄金分割数列（F(n+1)/F(n)的极限是1:1.618，即黄金分割率），指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……。在数学上，斐波纳契数列以如下被以递归的方法定义：
F(0)=0，F(1)=1，F(n)=F(n-1)+F(n-2)（n≥2，n∈N*）
递归实现——自上而下
在很多C语言教科书中讲到递归函数的时候，都会用Fibonacci作为例子。因此很多程序员对这道题的递归解法非常熟悉，看到题目就能写出如下递归求解的代码：
long Fibonacci(long n) //递归算法 { if(n<=1) return n; //终止递归的条件 else return Fibonacci(n-1) + Fibonacci(n-2);//递归步骤 }
但是，教科书上反复用这个题目来讲解递归函数，并不能说明递归解法最适合这道题目。我们以求解F(10)作为例子来分析递归求解的过程。要求得F(10)，需要求得F(9)和F(8)。同样，要求得F(9)，要先求得F(8)和F(7)……我们用下面的树形结构来表示这种依赖关系
F(10)
/ \
F(9) F(8)
/ \ / \
F(8) F(7) F(7) F(6)
/ \ / \
F(7) F(6) F(6) F(5)
我们不难发现在这棵树中有很多结点会重复的，而且重复的结点数会随着n的增大而急剧增加。这意味这计算量会随着n的增大而急剧增大。例如，在递归计算F(10)时，F(3)的值被计算了21次。而在递归计算F(30)，这个调用的次数是骇人的317811次！这些个计算实际上只有一次是必要的，其余的纯属浪费！
事实上这个递归算法的时间复杂度是指数级Ω(φn)，φ=1.618（1:1.618=0.618称为黄金分割率）。
迭代算法——自底向上
下面的程序使用一个简单循环迭代来代替递归，这个非递归的形式不如上文给出的递归简单，也不太符合Fibonacci的递归定义，但是，它的运行速度提高了特别多！
迭代算法的源码如下：
// 计算斐波那契数列的非递归算法(迭代) long Fibonacci(long n) { if(n<=1) return n; // Fib(0)或Fib(1)的情况 long FibCurrent, FibTwoBack = 0, FibOneBack = 1; // 用数组保存程序更简洁，但不能明显的看出迭代的思想 for(int i=2 ; i<=n ; i++) // n≥2的情况 { FibCurrent = FibOneBack + FibTwoBack; // 计算Fib(i)=Fib(i-1)+Fib(i-2) /* 下面的保存顺序不能对调 */ FibTwoBack = FibOneBack; // 保存Fib(i-1)作为下趟的Fib(i-2) FibOneBack = FibCurrent; // 保存Fib(i)作为下趟的Fib(i-1) } return FibCurrent; }
显然，这个算法的时间复杂度为O(n)，相比于前面指数级的递归算法，有了质的飞跃。
事实上，这还不是最快的算法。还有一种时间复杂度是O(logn)的方法
转化为特征矩阵乘方——分治策略 + 矩阵快速幂
由数学归纳法易证：
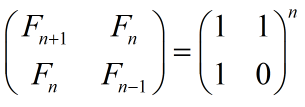
问题转化为求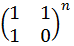
，继而就求出了F(n)。
对于乘方问题我们利用分治策略优化有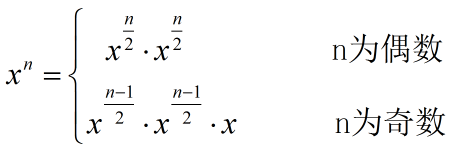 
运行时间递归式：T(n) = T(n/2) + θ(1) （同二分搜索一样） 用主方法接得T(n) = θ(logn)
利用对特征矩阵乘方优化的方法可以得到最小的运行时间复杂度O(logn)，代码如下：
class Matrix // 自定义2×2矩阵类 { public: unsigned int a11, a12, a21, a22; // 矩阵元素 Matrix(int a, int b, int c, int d) :a11(a), a12(b), a21(c), a22(d) {}// 构造函数 Matrix operator*(const Matrix &other) // 重载矩阵的乘法 { Matrix result(0, 0, 0, 0); result.a11 = a11*other.a11 + a12*other.a21; result.a12 = a11*other.a12 + a12*other.a22; result.a21 = a21*other.a11 + a22*other.a21; result.a22 = a21*other.a12 + a22*other.a22; return result; } }; Matrix MatrixPow(const Matrix &A, unsigned int n)// 计算矩阵A的n次方(分治策略,此处自底向上迭代) { Matrix result(1, 0, 0, 1); // 单位矩阵 Matrix tmp = A; while (n) { if (n & 1) // &为按位"与"运算,如果n为奇数 result = result * tmp;// 单乘一次矩阵 tmp = tmp * tmp; n = n >> 1; // n右移一位,相当于n/2(向下取整) } return result; } unsigned int Fibonacci(int n) { if (n <= 1) return n; Matrix A(1, 1, 1, 0); // 特征矩阵 Matrix result = MatrixPow(A, n); // 计算矩阵A的n次方 return result.a12; // Fn即为结果矩阵中第一行第二例上的元素 }
参考资料： 《MIT算法导论公开课》第三集——分治法
《编程之美》P163
《剑指offer》P73
