向量数学
(惯例感谢godot,线性代数大学必修课~~~~~~)
简介
本教程是一个简短而实用的线性代数介绍,因为它适用于游戏开发。线性代数是研究向量及其用途的学科。矢量在二维和三维开发中都有许多应用,Godot对它们的应用非常广泛。要成为一名优秀的游戏开发者,对向量数学的理解是必不可少的。
注解
本教程 不是 线性代数的正式教科书。我们将只关注它如何应用于游戏开发。要更全面地了解数学,请参见 https://www.khanacademy.org/math/linear-algebra
坐标系统(2D)
在2D空间中,使用水平轴(“x”)和垂直轴(“y”)定义坐标。2D空间中的特定位置被写成一对值,如``(4, 3)``。
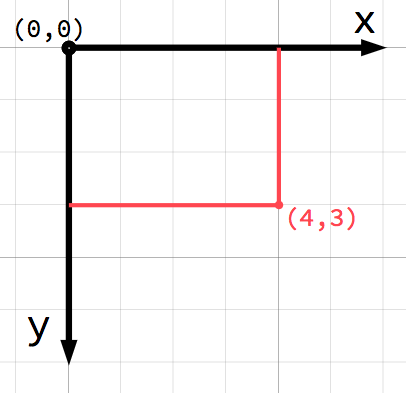
注解
如果你是计算机图形学的新手,你可能会觉得很奇怪, y 轴的正方向是 向下,而不是向上(你在数学课上学到的就像那样)。然而,这在大多数计算机图形应用程序中是常见的。
二维平面上的任何位置都可以用一对数字来表示。然而,我们也可以将位置 (4, 3) 看作是从 (0, 0) 点或 原点 出发的 偏移 。画一个箭头从原点指向点:
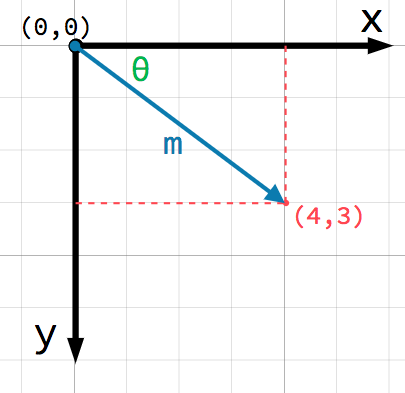
这是一个 向量 。向量表示许多有用的信息。除了告诉我们点在 (4, 3) 之外,我们还可以把它看成角度 θ 和长度(或幅度) m。在这种情况下,箭头是一个 位置向量 -它表示空间中相对于原点的位置。
关于向量,需要考虑的一个重要点是它们仅表示**相对**方向和大小。没有一个向量的位置的概念。以下两个向量相同:
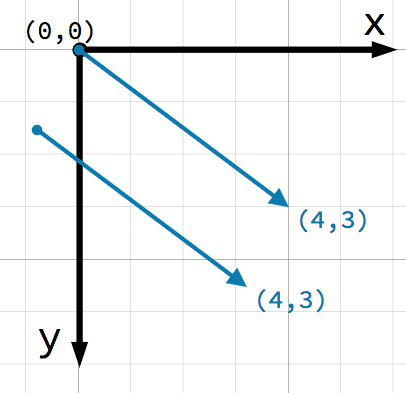
这两个向量都表示向右4个单位,在某个起始点以下3个单位。不管你在平面上画哪个向量,它总是代表一个相对的方向和大小。
向量运算
您可以使用任意一种方法(x和y坐标或角度和大小)来引用向量,但是为了方便起见,程序员通常使用坐标表示法。例如,在Godot中,原点是屏幕左上角,因此要将一个名为``Node2D`` 的2D节点向右放置400像素,向下放置300像素,请使用以下代码:
$Node2D.position = Vector2(400, 300)
Godot支持 Vector2 和 Vector3 分别用于2D和3D。本文讨论的数学规则同样适用于这两种类型。
- 成员访问
向量的各个组成部分可以直接通过名称访问。
# create a vector with coordinates (2, 5)
var a = Vector2(2, 5)
# create a vector and assign x and y manually
var b = Vector2()
b.x = 3
b.y = 1
- 添加向量
当两个向量相加或相减时,相应的分量相加:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
我们也可以通过在第一个向量的末尾加上第二个向量来直观地看到这一点:
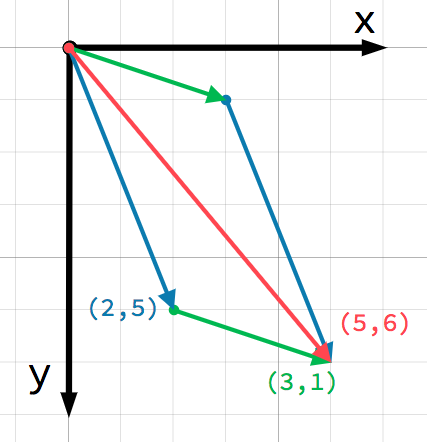
注意,加法 a + b 和 ``b + a``得到的结果是一样的。
- 标量乘法
注解
矢量表示方向和幅度。仅表示幅值的值称为 标量。
一个向量可以乘以一个标量:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
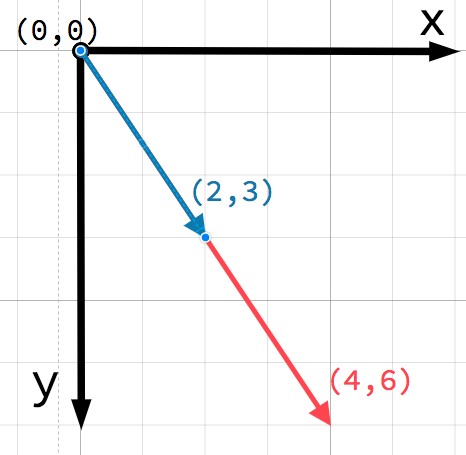
注解
向量乘以标量不会改变它的方向,只会改变它的幅值。这就是缩放向量的方法。
实际应用
让我们看看向量加法和减法的两种常见用法。
- 移动
矢量可以表示具有大小和方向的任何量。典型的例子有:位置、速度、加速度和力。在这幅图像中,在第一步的飞船有一个位置向量为``(1,3)``和一个速度向量为``(2,1)``。速度矢量表示船舶每一步移动的距离。通过将速度加到当前位置,我们可以求出步骤2的位置。
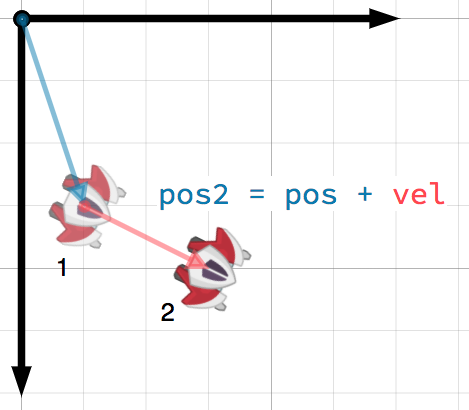
小技巧
速度测量单位时间内位置的变化。新的位置是通过在前一个位置上增加速度来找到的。
- 指向一个目标
在这个场景中,您有一个坦克,希望它的炮塔指向机器人。从机器人的位置减去坦克的位置就得到了从坦克指向机器人的矢量。(向量加减原则)

小技巧
要找到从 A 指向 B 的向量,请使用 B - A。
单位向量
一个 大小 为 1 的向量称为 单位向量 。它们有时也被称为 方向向量或 法线 。当你需要跟踪一个方向时,单位向量是有用的。
归一化
归一化 矢量意味着在保持其方向的同时将其长度减少到 1 。这是通过将每个分量除以其大小来完成的:
var a = Vector2(2, 4)
var m = sqrt(a.x*a.x + a.y*a.y) # get magnitude "m" using the Pythagorean theorem
a.x /= m
a.y /= m
由于这是一种非常常见的操作, Vector2 和 Vector3 提供了归一化的方法:
a = a.normalized()
警告
因为归一化需要除以向量的长度,所以不能对长度为“0”的向量进行归一化。试图这样做会导致错误。
反射
单位向量的一种常见用法是表示 法线 。法向量是垂直于曲面的单位向量,定义了曲面的方向。它们通常用于照明、碰撞和涉及表面的其他操作。
例如,假设我们有一个移动的球,我们想从墙上或其他物体上弹回来:
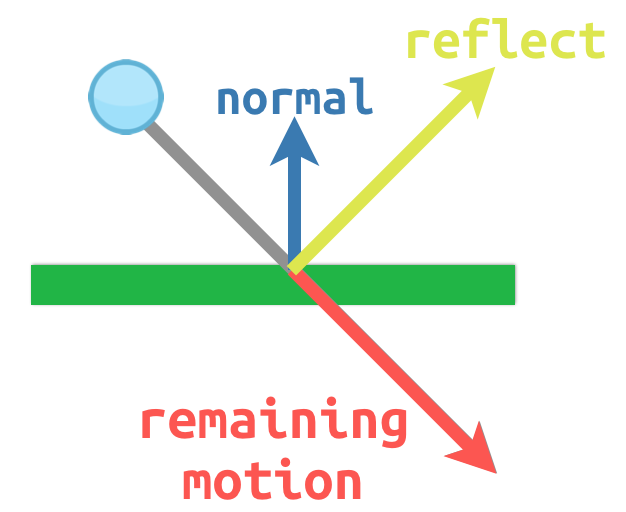
因为这是一个水平曲面,所以曲面法线的值为 (0, -1) 。当球碰撞时,我们取它的剩余运动(当它撞到表面时剩余的量),用法线反射它。在Godot中, Vector2 类有一个 bounce() 方法来处理这个问题。上图有一个使用 KinematicBody2D 的GDScript示例:
# object "collision" contains information about the collision
var collision = move_and_collide(velocity * delta)
if collision:
var reflect = collision.remainder.bounce(collision.normal)
velocity = velocity.bounce(collision.normal)
move_and_collide(reflect)
点乘
点乘 是向量数学中最重要的概念之一,但经常被误解。点乘是对两个向量的操作,它返回一个 标量。与同时包含大小和方向的矢量不同,标量值只有大小。
点乘公式有两种常见形式:

以及

然而,在大多数情况下,使用内置方法是最容易的。注意,两个向量的顺序并不重要:
var c = a.dot(b)
var d = b.dot(a) # these are equivalent
当与单位向量一起使用时,点积是最有用的,使得第一个公式减少到仅有 cosθ。这意味着我们可以使用点积来告诉我们关于两个向量之间的角度的一些信息:
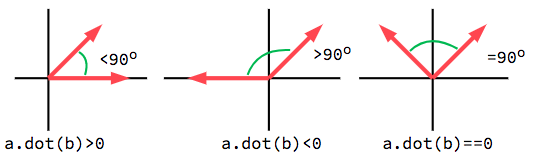
当使用单位向量,结果总是会在 -1 (180°) 和 1 (0°) 之间。
面向问题
我们可以利用这个事实来检测一个物体是否面向另一个物体。在下图中,游戏角色 P 试图避开僵尸 A 和 B 。假设一个僵尸的视野是 180° , 他们能看到游戏角色吗?
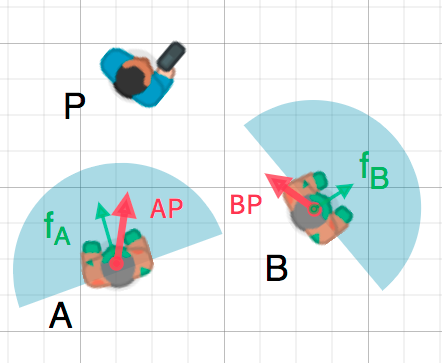
绿色箭头 fA 和 fB 是 单位向量 表示僵尸的朝向,蓝色半圆表示其视野。对于僵尸 A ,我们使用 P - A 找到指向玩家的方向向量 AP 并将其归一化。如果这个向量和面向向量之间的夹角小于90°,那么僵尸可以看到玩家。
在代码中是这样的:
var AP = (P - A).normalized()
if AP.dot(fA) > 0:
print("A sees P!")
叉乘
和点乘一样, 叉乘 是对两个向量的运算。然而,叉乘的结果是一个方向垂直于这两个向量的向量。它的大小取决于它们的相对角度。如果两个向量是平行的,它们叉乘的结果就是零向量。


叉乘是这样计算的:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
使用Godot,您可以使用内置的方法:
var c = a.cross(b)
注解
在叉乘中,顺序很重要。a.cross(b) 和 b.cross(a) 的结果不一样。得到的向量指向相反的方向。
法线计算
叉乘的一种常用方法是在三维空间中求平面或曲面的表面法向量。如果我们有三角形 ABC 我们可以用向量减法找到两条边 AB 和 AC。通过叉乘, AB x AC 得到一个垂直于这两个向量的向量:表面法向量。
下面是一个计算三角形法线的函数:
func get_triangle_normal(a, b, c):
# find the surface normal given 3 vertices
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
指向目标
在上面的点乘部分,我们看到了如何用它来求两个向量之间的夹角。然而,在3D中,这是不够的。我们还需要知道绕哪个轴旋转。这可以通过计算当前方向与目标方向的叉乘得到。得到的垂直向量是旋转轴。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号