0610学习笔记 张宇基础30讲——第13讲常微分方程

 微分方程的概念

　　微分方程：一般来说函数分为显函数和隐函数，显函数为y=f(x)，求导可得y' = x的式子，求积分可以得到原函数。而隐式一般写成F(x,y) = 0，隐函数的确定是找到一个在一定条件下满足一个x对应1个y的函数y=f(x)（单值函数），则称y=f(x)为隐函数。隐式写法在求导后会变成全家福F(x,y,y',……,yn')=0，这个时候这种含有x,y到y的n阶导的形式叫做微分方程。本讲内容在研究如何通过微分方程求原函数y=f(x)。为什么不能积分求原函数呢？因为全家福中包含x和y，没办法分离他们，因此没办法通过积分求原函数。

　　常微分方程：微分方程中的未知函数y为一元函数

　　微分方程的阶：微分方程中最高阶导数的阶数

　　微分方程的解：解y=f(x)带入到方程中能恒成立的

　　　　通解：y=f(x)中独立变量c的个数等于微分方程的阶数，则y=f(x)为微分方程的通解

　　　　特解：将初始条件带入通解中求出的解为特解（通解中的常数具体取值）

一阶微分方程的求解【如果发现题目四种都不符合，可以思考能否变量互换位置，比如遇到 lny】

　　变量可分离型：物以类聚

　　可化为变量可分离型：换元+物以类聚

　　　　① dy/dx = f(ax+by+c)：令u=ax+by+c，du/dx = a + dy/dx，带入原方程得 du/dx - a = f(u) ——> du/(a+f(u)) = dx、再物以类聚

　　　　② dy/dx = φ(y/x)：方程化简，看能否变为φ(y/x)的形式，可以的话令u=y/x，dy/dx = du/dx*x + u，再物以类聚

　　一阶线性微分方程【似乎没见到特解？】：y' + p(x)*y = q(x)【思路：e^狗、(uv)' = u' * v + u * v' 】，通解公式：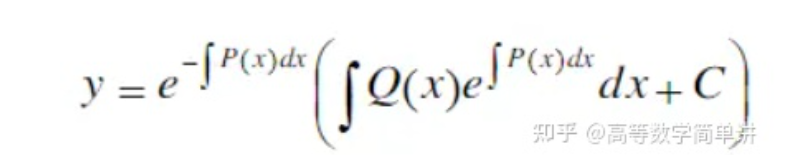

　　伯努利方程：y' + p(x)*y = q(x)*（y^n）：① 恒等变换，处理掉等式右边的y^n  ② 换元法，恒等变换后令z=与p(x)相乘的数  ③ 套一阶线性微分方程公式

 

二阶可降阶微分方程的求解：y'' = f(x,y')【不含y】 、 y'' = f(y,y')【不含x】

　　① y'' = f(x,y')【不含y】：令y' = p，则y'' = p'，则有p' = f(x,p)。将p和p'带入到方程，利用一阶微分方程求解方法做题

　　②  y'' = f(y,y')【不含x】：令y' = p，则y'' = (dp/dy)*(dy/dx) = (dp/dy)*p，则有(dp/dy)*p= f(y,p)。将y''和y'带入到方程，利用一阶微分方程求解方法做题

 

高阶线性微分方程的求解:

　　齐次：微分方程等号右边为0

　　非齐次：等号右边≠0

　　线性：微分方程中y,y'到y的n阶导全都是1次且进行线性操作（加减）

　　变系数：y'+p(x)y = q(x)，此时p(x)为变系数

　　常系数：y'+px = q，此时p为常系数

 

　　解的结构（二阶举例）：

　　① 若y1(x)和y2(x)为微分方程的两个解且y1(x)/y2(x)≠C（两个解线性无关），则微分方程的通解为y(x) = C1*f1(x)+C2*f2(x)【齐次】

　　② 若y(x) = C1*f1(x)+C2*f2(x)为微分方程的通解，y*(x)为微分方程的特解，则微分方程的通解为：y(x) = C1*f1(x)+C2*f2(x) + y*(x)【通解+特解】【非齐次】

　　③ 若微分方程=f1(x) + f2(x)，且f1*(x)为f1(x)的解，f2*(x)为f2(x)的解，则微分方程的通解为: f1*(x) + f2*(x)  P201例13.8

　　

　　题目类型：二阶常系数齐次微分方程的通解、二阶常系数非齐次微分方程的特解、n阶常系数齐次微分方程的解

　　二阶常系数齐次微分方程的通解【y''+py'+qy = 0】：将y=e^(λx)带入方程，提出公共部分e^(λx)，剩下的部分为特征方程，利用Δ求出通解。

　　　　Δ>0：y = C1*e^(λ1x) + C2*e^(λ2x)【特征解为λ1，λ2】

　　　　Δ=0：y = (C1+C2)*e^(λx)【特征解为λ1=λ2】

　　　　Δ<0：y = e^(αx)【C1*cosβx + C2*sinβx】【特征解为a±bi】

　　二阶常系数非齐次微分方程的特解【y''+py'+qy = f(x)】：

　　　　① f(x) = e^(λx)*【Pn(x)】：① e^(λx)照抄、② 找Pn(x)的n次多项式：x的n次多项式为AX+B，C的n次多项式为A，x^2的n次多项式为AX^2+BX+C

　　　　　　　　　　　　　　　　 ③ x^k（一看二算三对比，一看：看抄下来的α，二算：算此微分方程的齐次方程的特征解【求出特征方程后得-b±根号(b^2-4ac)/2a】，三对比：k=0:α！=特征解，k=1:α=其中一个特征解，k=2：α=两个特征解=二重根）

　　　　　　特征解：y* = e^(λx) * Qn(x) * x^k

　　　　② f(x) = e^(λx)*【Pn(x)*cosβx + Pm(x)*sinβx】：

　　　　　　　　　　　　　　　　① e^(λx)照抄、② 找max{ Pn(x)，Pm(x) }的n次多项式Q l (x)：x的n次多项式为AX+B，C的n次多项式为A，x^2的n次多项式为AX^2+BX+C

　　　　　　　　　　　　　　　　 ③ x^k（一看二算三对比，一看：看抄下来的α，二算：算此微分方程的齐次方程的特征解【求出特征方程后得-b±根号(b^2-4ac)/2a】，三对比：k=0:α±b不是特征解，k=1:α±b是特征解）

　　　　　　特征解：y* = e^(λx) *【Q l (x)*cosβx + Q l (x)*sinβx】* x^k

　　n阶常系数齐次微分方程的解【yn + p1yn-1 + p2yn-2 + …… + pny = 0】：【一般互推，通解xx的根是啥，根为xx的通解是啥】

　　　　① 特征根为单实根λ：微分方程中通解对应一项C*e^(λx)

　　　　② 特征根为k重实根λ：微分方程中通解对应一项（C1+c2x+c3*x^2+……+ck*x^k-1）e^(λx)

　　　　③ 特征根为单复根α±β：微分方程中通解对应两项e^(λx)【C1*cosβx + C2*sinβx】

　　　　④ 特征根为k重复根α±β：e^(λx)【（C1+c2*x+c3*x^2+……+ck*x^k-1）*cosβx +（D1+D2*x+D3*x^2+……+Dk*x^k-1）*sinβx】

　　　　得出λ之后，要写出y的方程，因为y=e^(λx)，特点是无论y求几阶导，永远只有λ的次数在改变。也就是若得出特征方程为λ*（λ-1）=0，则立刻有微分方程：y''-y=0【ps：特征方程是将根全部乘起来，比如得出λ=0为二重根和根为1±2i，则立刻有特征方程：λ^2(λ-(1-2i))*(λ-(1+2i))=0】例题P202 13.9