0509学习记录张宇基础30讲——第八讲一元函数积分学的概念与计算

这一讲简直又难又离谱，这里做个总结归纳

 

概念：【积分的证明题抓紧Δx和积分的几何意义】

不定积分的定义：全体原函数（没有积分域）

不定积分（原函数）存在定理【要求会证】：1. 若f(x)连续，则区间内必有原函数、2. 若f(x)含有第一类间断点或无穷间断点，则区间内原函数必不存在【振荡间断点可能有原函数，关键是看能否写出原函数的形式】

定积分的定义：面积（分割、近似、求和、取极限）

定积分存在定理：1. 若f(x)在[a,b]上连续，则定积分必然存在、2. 若f(x)在[a,b]上为单调函数，则定积分必然存在、3. 若f(x)在[a,b]上有界且有有限个间断点，则定积分必然存在

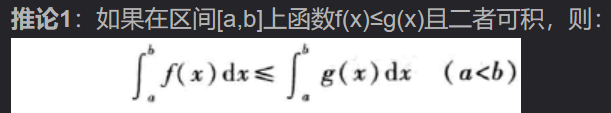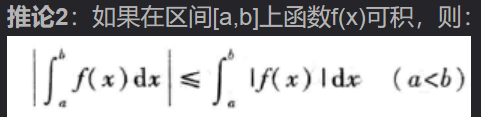定积分的性质：区间长度、线性可加【   】、积分可加、积分保号性【 、 】、估值定理【  ，其中m、M为区间上的最小值和最大值】、中值定理【  】

变限积分的定义：积分的上限/下限/上下限 不确定

变限积分的性质【要求会证】：1. 若f(x)在[a,b]上可积，则F(x)在[a,b]上连续 、2. 若f(x)在[a,b]上连续，则F(x)在[a,b]上可导

辅助记忆图：补

变限积分求导公式：

反常积分的定义：定积分要求区间和被积函数有界，则区间无界的积分称为无穷区间上的反常积分，函数无界的积分称为无界函数的反常积分

无穷区间上反常积分的概念与敛散性：反常积分的极限存在则收敛，不存在则发散。若为[-∞，+∞]，则要分为[-∞，0]和[0,+∞]，因为一个区间内不能出现两个特殊点【无穷或无定义点】

无界函数的反常积分的概念与敛散性：反常积分的极限存在则收敛，不存在则发散。若区间内部有瑕点，则按瑕点把区间划分开

 

计算：

不定积分的计算方法：【5】

　　1. 基本积分公式【10大条，p116-117】

　　2. 凑微分（向后）

　　3. 换元法（向前）【5】

　　　　1. 三角函数代换（x换成与三角函数有关的表达，一般常见于（a^2±C）^2）（和三角函数有关的式子，要么换元( t=……、x=asint）、要么区间再现、要么升降次）ps：三角中sin^2 x除了换成cos^x，还可以换成cos^2 x * tan^2 x（常见于式子中有tanx、cosx、sinx同时出现）

　　　　2. 等价代换（被积函数含有根式，直接变成根号内两式的平方相加减）后做三角代换 / 等价代换（分子分母同乘，比如：1/（1+sinx）dx，同乘后：1/cos^2x dx- sinx/cos^x dx）

　　　　3. 根式代换：令根式 = t （换元）/ 对于分子分母都含有相同根式：同乘根式的最小公倍数

　　　　4. 倒带换（没遇到过，有再补充例子）

　　　　5. 复杂函数（被积函数中含有反对幂指三）直接代换为t，若为（反对幂指三）中的两个相乘，优先考虑分部积分法【u的优先级：反对幂指三】

　　4. 分部积分法【5】

　　　　1. u的优先级：反对幂指三

　　　　2. 分部积分法的推广公式：表格法【上面一直求导，下面一直求原函数，最后一项为积分形式，其余直接相乘】

 

　　5. 有理函数的积分

定积分的计算方法：【3】

　　1. 牛顿莱布尼兹公式 ： 

 

　　2. 换元法

　　3. 分部积分法【巧用区间性质】

　　　　1. 奇偶性【对称区间】

　　　　2. 周期性【常见于T，Π】

　　　　3. 区间再现公式：

　　　　4. 点火公式（奇数发射成功*Π/2，偶数发射失败）：

　　

　　　　　　

 

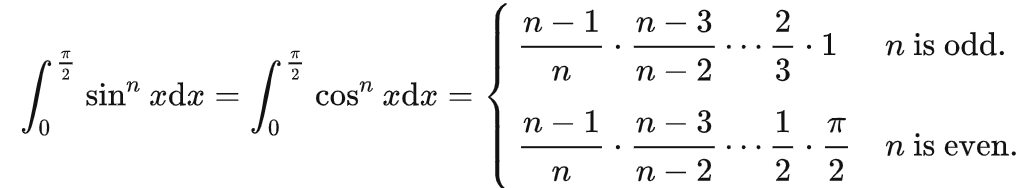
 【例8.6：f(x) = 幂函数+幂函数*积分，此时两边同时积分，就能求出积分值，因为此时f(x)中的积分相当于一个常数，直接提出来】

反常积分的计算方法：有瑕点就把区间划分开，没有瑕点就求出原函数然后把区间两端带进去

反常积分的敛散性判断：补图

 　　我的一些个人tips：主要是分为等价和比较两类方法。等价就是通过常见的等价无穷小来化简式子；比较就是对于式子中含有e^x、lnx、x这种，一眼判断出式子的变化主要是取决于什么。比如x^n/(e^x)^n，（e^x）趋于无穷的速度明显远超x^n，所以直接看成1/(e^x)^n