0418-0420学习笔记 张宇基础30讲——第三讲函数极限与连续性
函数极限:
ε(epsilon),δ(delta)
邻域:
一维:
邻域:数轴上以x0为中心的任何开区间(δ邻域:存在一个点x0,存在一个数 δ ,若x∈(x0-δ,x0+δ),则x属于x0的δ邻域)
去心邻域:存在一个点x0,存在一个数 δ ,若x∈(x0-δ,x0)(x0,x0+δ),则x属于x0的去心邻域
二维:
δ邻域:存在一个点P0(x0,y0) ,存在一个数 δ ,P(x,y)到P0的距离小于δ,则x属于x0的δ邻域
去心邻域:存在一个点P0,存在一个数 δ ,若存在一个点P,使得0< | P0-P | <δ,则P属于P0的去心邻域
定义:①任意 ε > 0 ②存在 δ > 0 ③若 | x - x0 | < δ ④ | f (x) -A | < ε
存在一个常数A,若对于给定的任意整数ε(无论多小),总存在正数 δ,使得当 0 < | x - x0 | < δ 时,总满足 | f (x) - A | < ε,则A为函数f(x)当x—>x0时的极限值

函数极限存在的充要条件:左极限=右极限(当x趋于某一点时函数极限存在和该点没有任何关系)【证明函数极限存在的方法:① 单调有界法则【单调有界的函数/数列必有极限/收敛】——先证明函数有极限(单调性递增递减,有界为A),再把极限值算出来 (将A带入题目给的条件)② 夹逼准则】
等式脱帽法:当x趋于x0时,lim f(x) = A可以得出 f(x) = A + α(x),其中 lim α(x)= 0
ps:α(x)不一定是x的高阶无穷小,具体多大还是得看对f(x)-A求极限之后x的次数是多少(具体问题具体分析)
性质:
① 唯一性:函数f(x)当x—>x0存在极限值时,极限值唯一【左右极限不相等导致极限不存在的例子:① x->∞, lim e^x、② x->∞,lim sinx / |x| 、③ x->∞,lim arctanx、④ x->0,lim [x]】
② 局部有界性:函数f(x)当x—>x0存在极限值时,若存在正整数M和δ,则函数在 0< |x-x0| < δ 处有f(x)<=M
③ 局部保号性:当函数f(x)在x—>x0时的极限值为 A( A>0 / A < 0 ),则 f ( x ) > 0 / f ( x ) < 0 ;当 f ( x ) >= 0 / f ( x ) <= 0时,A>=0 / A<=0
证明局部保号性:当x趋于x0时,有f(x) = A,存在一个无论有多小的正整数δ,则有 | f(x) - A | < δ,即 - δ < f(x) - A < δ。设 δ = A/2,则有 - A/2 < f(x) - A < A/2,即A/2 < f(x) < 3/2*A,而A>0,因此 f(x)>0。【或许有人有疑问,若δ取2A,则f(x)不就是大于一个负数了吗?不就无法证明f(x)大于0了吗?但其实f(x)的取值和A是无比接近的,取值不会因为所给的范围改变而改变,比如0<1<2和-100<1<100是一个道理,我们证明了0<1<2,然后看着-100<1<100来怀疑1是否真的大于0是没必要的】
运算规则:【注意大前提——红色部分,比如①若有lim[(A+B)/C],不能随便拆分成limA/C+limB/C,要判断limA/C和limB/C是否存在,存在才能拆;②若给出lim(a+b) = 2,lim(a-b) = 4,求a,b。不能直接拆分成lim a + lim b = 2,lim a - lim b = 4,然后加减。必须要u = a+b,v = a-b,lim u = 2 , lim v = 4,此时lim u 和lim v存在,则有lim u + lim v = lim (u+v) = 2+4 = 6,即lim 2a = 6,解出lim a = 3】
若存在 lim f ( x ) = A,lim g ( x ) = B,则有:
① lim [ f ( x ) * g ( x ) ] = A * B
② lim [ k* f ( x ) + g ( x ) ] = k * lim f ( x ) + lim g ( x ) = k*A + B
③ lim [ f ( x ) / g ( x ) ] = lim f ( x ) / lim g ( x ) = A / B
④ lim [ f ( x ) ^ n ] = [ lim f ( x ) ] ^ n
夹逼准则:(也可用于证明函数极限存在)
若 h ( x ) <( / <= ) f ( x ) < ( / <= ) g ( x ),且 lim h ( x ) = A, lim g ( x ) = A,则 lim f ( x ) = A
洛必达法则:
法则1:
① 0 / 0
② 函数 f ( x ),g ( x ) 可导
③ lim f ‘ ( x ) / g ‘ ( x ) 存在(若不存在,不证明 lim f ( x ) / g ( x ) 不存在,只能说明不能用洛必达法则来求极限)
则 lim f ‘ ( x ) / g ‘ ( x ) = lim f ( x ) / g ( x ) ——> 若求出来的 lim f ‘ ( x ) / g ‘ ( x )仍属于0 / 0,且满足洛必达法则条件,则可继续洛
法则2:
① ∞ / ∞
② 函数 f ( x ),g ( x ) 可导
③ lim f ‘ ( x ) / g ‘ ( x ) 存在(若不存在,不证明 lim f ( x ) / g ( x ) 不存在,只能说明不能用洛必达法则来求极限)
则 lim f ‘ ( x ) / g ‘ ( x ) = lim f ( x ) / g ( x ) ——> 若求出来的 lim f ‘ ( x ) / g ‘ ( x )仍属于∞ / ∞,且满足洛必达法则条件,则可继续洛
泰勒公式:
公式:
sinx 、 cosx、arcsinx、arccosx、tanx、arctanx、ln ( 1 + x )、e^x、( 1 + x )^ a

展开原则:
① A/B型:上下同阶(上下展开到相同阶)
② A-B型:幂次最低(左右展开到相同阶且不同系数)例如:求当x趋于0,lim(x+sinx):x+sinx = x - (-sinx) =(泰勒)= x - (-x) = 2x。sinx没有继续展开是因为x和-x已经是同阶不同系数了
归结原则 / 海涅定理 :将数列极限与函数极限连接起来【看到求极限的地方是n趋于∞就应该意识到这个是数列的极限】。若函数f(x)存在极限A,且xn为函数定义域内的任意一个收敛于x0的子数列(按函数顺序),则当n趋于∞,f(xn) = A = 当x趋于x0的f(x),注意:xn不能取x0
例如:若极限lim sinx/x 存在,xn = 1/n 为 sinx / x 函数定义域内收敛于0的数列,且 xn = 1/n ≠ 0,则sin(1/n) / (1/n)收敛,且当x趋于0时,f(x) = sinx / x = A可以推出:当n趋于∞时,f(xn) = sin(1/n) / (1/n) = A
无穷小比阶:
定义:当x趋于x0或∞时,lim f(x) = 0,则f(x)为x趋于x0或∞时的无穷小
比阶:前提:lim f(x) = 0, lim g(x) = 0
① 若lim f(x)/g(x) = 0,则f(x)是比g(x)高阶的无穷小
② 若lim f(x)/g(x) = C ≠ 0,则f(x)是与g(x)同阶的无穷小
③ 若lim f(x)/g(x) = ∞,则f(x)是比g(x)低阶的无穷小
④ 若lim f(x)/ [g(x)]^k = C ≠ 0,则f(x)是g(x)的k阶无穷小
⑤ 若lim f(x)/g(x) = 1,则f(x)是g(x)等价无穷小,记为 f(x) ~ g(x) 【这条对我来说十分重要,以后当做题遇到等价转换的时候不确定,可以把这个公式带进去验算。比如今天做题遇到的:当x趋于0时,ln|x|是否等价于|x-1|——参考ln(1+x)~x。计算发现lim ( ln|x| / |x-1| )≠1,因此得出不等价】
无穷小运算准则:
① o(x^n) ± o(x^n) = o(x^n)
② o(x^m) ± o(x^l) = o(x^n) 【n = min {m,l} 】
③ o(x^m) * o(x^n) = o(x^(m+n))
④ o(x^m) = o(k*x^m) = k * o(x^m)
常用的等价无穷小:
当x趋于0时,sinx、tanx、arcsinx、arctanx、ln(1+x)、e^x-1 ~ x 、 (1+x)^α - 1 = αx(经典的√1+x - 1 = (1/2)*x) 、 1 - cosx ~ (1/2)*(x^2) 、 a^x - 1 ~ xlna(a^x导数为(a^x)*lna )
当x趋于1时,lnx ~ x-1
连续与间断:
连续点的定义:f(x)在x0的某一邻域内有定义(x,y都存在),且linf(x0) = f(x0),则函数在x0处连续。(我的理解似乎是错的:如果当x趋于x0时函数有左右极限,且左右极限=A,且f(x0) = A,则函数在x0处连续)【若函数在 [a , b] 上连续,则函数在 [a , b]上有极限、若函数在 (a , b) 上连续且当x在x->a+和x->b-时极限存在,则函数在 (a , b) 上有极限】
间断点的定义与分类:(间断点只看分段点(给明分段函数或分母中存在或直接为|x|、x^2、√x^2)和无定义点(分母为0,分子为lnx时x<0等))
① 可去间断点:函数左右极限相等但f(x0)≠A
② 跳跃间断点:函数左右极限不相等
③ 无穷间断点:函数左右极限至少一个为无穷
④ 振荡间断点:函数极限不存在且在一些数中反复横跳,比如当x趋于∞时的sinx
七种未定式:
①:0/0、∞ / ∞、0 * ∞ ———— 全部转化成 0 / 0 或 ∞ / ∞。然后考虑洛必达(看见x^100次方这种)、泰勒(看见sinx-tanx这种)、夹逼(看见 [x] )、等价代换(以下都是当x趋于0的情况:看见 ln sinx / x —— ln ( sinx + x / x) - 1 )~ sinx + x / x 、看见 e^tanx - e^sinx —— 换成e^x (e^tanx - sinx - 1) ~ e^x ( tanx - sinx ) 、 看见 x^x - (sinx)^x ——x^x (1-(sinx/x)^x) = - x^x ( (sinx/x)^x - 1) ~ x^x * x*ln( sinx/x )【这里用到的是( a^x - 1) ~ xlna,注意如果这里分子只有这个,则x^x可以直接替换成1,因为lim x^x = 1】
②:∞ - ∞:有分母就通分,没分母创造分母(做倒带换,u = 1/x)再通分

③:∞^0、0^∞、1^∞:前两个:u^v = e^ v*lnu ,最后一个:u^v = e^ v*(u-1)【看到根号就要有理化】
极限反求参数:已知函数的极限,且函数中含有未知数a,b。如:( a*x - b*x^2 + o (x^2) ) / x^2 = c,则上下为同阶无穷小,a*x为x^2的低阶无穷小,b*x^2为x^2的同阶无穷小,o (x^2)为x^2的高阶无穷小。除了同阶无穷小以外,本题中高阶无穷小和低阶无穷小的系数都需要为0.如果说f(x)是比g(x)高阶的无穷小,那么同阶和低阶系数就要为0
最近的刷题启示:
① 看到ln(sinx/x)这种求极限,泰洛都不行后可构造ln( (sinx+x) / x - 1 ) ~ (sinx+x) / x
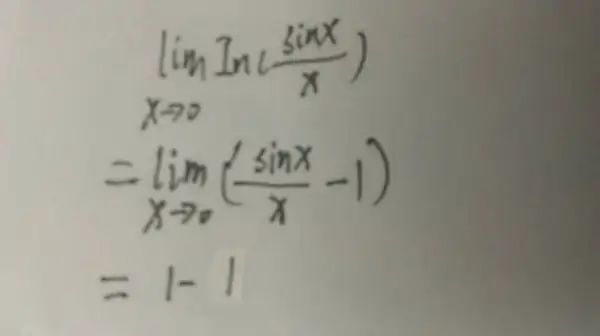
sinx/x = sinx/x -1 +1
② 看到 x^x - (sinx)^x —— - x^x * ( (sinx/x)^x - 1 ) ~ - x^x * ( x * ln( sinx / x ) )【提取公因式、等价无穷小:a^x -1 = xlna】
③ 本人尤其记不住:lim x^x = 1(当x->0)【e^(xlnx)】、a^x - 1 ~ x*lna
④ 做题步骤:1. 如果函数复杂,先看看能不能等价代换 、2. 判断极限属于哪种类型 、 3. 套方法,如果方法没用,试一下+1和-1之后能不能等价代换
⑤ 在求极限的时候,本人总是忘记要分情况讨论:x->0+、x->0-


 浙公网安备 33010602011771号
浙公网安备 33010602011771号