密码技术密码杂凑算法学习笔记
0、任务详情
-
使用Get笔记辅助听资源中的视频 “ch03 密码技术-03-密码杂凑算法”,整理总结Get笔记生成内容,修正识别错误
-
实践视频中相关命令,参考教材和网络资源以及AI工具,补充自己理解不好的内容,列出自己的贡献,理解标准中内容http://www.gmbz.org.cn/main/viewfile/20180108023812835219.html
-
编译运行相关代码,使用gdb运行相关代码,要和标准中内容对照,http://www.gmbz.org.cn/main/viewfile/20180108023812835219.html,提交相关截图
-
提交学习笔记markdown和pdf格式的学习笔记,命名规则:8位学号_姓名_密码技术密码杂凑算法学习笔记.md,8位学号_姓名_密码技术密码杂凑算法学习笔记.pdf
1、密码技术密码杂凑算法-GET笔记内容总结
单向函数
- 定义:正向计算容易,逆向运行困难的函数。例如,将盘子打碎容易,但恢复困难;数学中的模运算也是正向易、逆向难的例子。
- 实用单向函数考量:需均衡计算性能与破解强度。正向计算的容易程度体现函数计算性能,逆向计算的困难程度体现破解强度。杂凑函数可将任意大小数据转换为固定长度的杂凑值(哈希值),输入数据大小不限,输出长度固定,不可避免会出现杂凑值碰撞。
- 降低碰撞方法:一是增加杂凑值长度,但并非越长越好,需在性能优化和碰撞风险间平衡,如密码使用中128位安全强度足够,多数杂凑值为256位;二是提高杂凑函数质量,生成均匀分布的杂凑值以降低碰撞概率。
密码杂凑函数
- 定义与特性:既是单向函数也是杂凑函数,需满足逆向运算困难、构造碰撞困难。具有雪崩效应,即输入数据微小变化会导致输出数据巨大变化,严格雪崩效应指输入数据一位反转,输出数据每一位有50%概率变化。
- 设计模式:
- MD结构:对输入消息分组或分块,对每块进行压缩,最终输出固定长度哈希值。采用此结构的算法有MD5、SHA - 256及我国商密SM3等。
- 海绵结构:主要用于特定应用,能通过吸收和挤压将任意长度输入转换成任意长度输出(实际输出不会过长)。
- 应用 - 完整性保护:用于数据完整性保护,通过检查数据是否变动解决问题。基本过程是输入数据D、杂凑和S及杂凑函数,重新计算数据D的杂凑值S’,若S’与S相同,说明数据D完整,否则数据被修改。MD结构的密码杂凑算法易受长度延申攻击,建议不使用单向杂凑函数处理包含机密和公开数据的信息,而使用消息验证码等算法。
SM3密码杂凑算法
- 标准与常量函数:我国采用的密码杂凑函数标准,速度长度L小于2的64次方,输出消息经填充迭代压缩生成256比特杂凑值。行业标准是GMT00040,国标是32905,算法设计包含常量IV、布尔函数FF、GG,置换函数P0、P1。
- 数据填充:因SM3是MD结构需分组,实际消息不一定是分组整数倍长度,所以要填充。填充方法是在消息后添一个1,再填K个0,使L + 1 + K等于448(512的整数倍减64)的最小非负整数,最后添加64位L的二进制比特串。
- 分组计算拓展:以生活场景举例说明向上取整算法在密码技术中的应用,如将N位数据按每组M位分组,组数为(N + M - 1) / M 。在SM3算法中,将明文按512比特分组,组数计算为(L + 511) / 512 。
- 迭代压缩:把填充后的消息按512比特一组分组,分成N组(N = (L + K + 65) / 512 或 (L + 511) / 512 ),通过迭代方式,利用压缩函数,从初始向量V0开始,对每组消息进行计算,生成132个消息字,最终输出256比特杂凑值。
- 实现方式:
- 一段式:按标准方法实现,但需注意验证,可与open SSL计算结果对照。
- 三段式:因消息可能很长,计算机内存无法一次性处理,将SM3算法分为初始化(emit)、多次更新(update)、结束(final)三段。消息填充在final阶段进行。我国商密标准GMT0018中规定的哈希算法SM3也是三段式。
H MAC
- 定义与应用:带密钥的杂凑函数,可用于消息认证。消息认证有消息认证码、消息加密、数字签名三种方法,H MAC是使用单向散列函数构造消息认证码的方法,1996年提出,1997年作为RFC 2104公布,在众多密码协议中广泛应用,成为事实上的网络安全标准。
- 构造与运算:可使用多种高强度单向散列函数构造,如SM3等。利用密钥和明文进行两轮核心运算,运算步骤分为七步,涉及标准中定义的固定值ipad和opad 。实现方式也是三段式,同样需与open SSL对照测试。
📅 章节概要
00:00:09 引入密码加速算法及单向函数概念
主讲人开场表明要讲解密码技术中的密码加速算法,先介绍单向函数。阐述其定义为正向计算容易、逆向运行困难的函数,通过打碎盘子易恢复难的类比,以及数学模运算的例子辅助理解。同时指出实用单向函数要均衡计算性能与破解强度,介绍杂凑函数可将任意大小数据转为固定长度杂凑值(哈希值),输入不限大小输出长度固定,会出现杂凑值碰撞,还提及降低碰撞的方法,包括平衡杂凑值长度与性能,以及提高杂凑函数质量。
00:03:22 讲解密码杂凑函数
说明密码杂凑函数既是单向函数又是杂凑函数,要满足逆向运算和构造碰撞困难的要求。介绍其两种设计模式,MD结构是对输入消息分组压缩输出固定长度哈希值,列举MD5、SHA - 256及我国SM3等算法采用此结构;海绵结构主要用于特定应用,能转换任意长度输入为输出。强调密码杂凑算法要有雪崩效应,以SM3算法计算hello word和hello vivo字符串为例展示雪崩效应。还讲解了密码杂凑算法用于完整性保护的原理及基本过程,同时提到MD结构算法易受长度延申攻击及应对建议。
00:08:19 聚焦SM3密码杂凑算法标准与常量函数
介绍SM3是我国采用的密码杂凑函数标准,说明其速度长度及输出杂凑值长度,给出行业标准和国家标准编号。讲解算法设计包含的常量IV、布尔函数FF、GG,置换函数P0、P1 。
00:09:26 SM3算法的数据填充
因SM3是MD结构需对数据分组,而实际消息长度不一定符合分组要求,所以要进行填充。详细讲解填充方法,先在消息后添1,再填K个0使消息长度满足特定条件,最后添加64位消息长度的二进制比特串。通过ABC消息填充的例子,具体演示填充过程。
00:12:15 分组计算拓展及在SM3中的应用
以团队订房间的生活场景举例,说明C语言向下取整特性下,在密码技术实现中模拟向上取整的算法,即(N + M - 1) / M 。并拓展到不同场景应用,如二进制转十六进制分组及SM3算法中明文分组的计算。
00:14:19 SM3算法的迭代压缩
讲解SM3把填充后的消息按512比特一组分组,通过公式计算分组数。介绍迭代压缩过程,从初始向量V0开始,利用压缩函数,对每组消息进行计算,生成132个消息字,最终输出256比特杂凑值,还列出相关计算方法和压缩函数流程。
00:15:49 SM3算法的实现方式 - 一段式
提出SM3算法在工程实现可采用一段式,即按标准方法实现。同时提醒注意验证,可将相同消息用open SSL计算并与自己编写程序的结果对照,确保程序正确。
00:16:17 SM3算法的实现方式 - 三段式
讲解因消息可能很长,计算机内存无法一次性处理,所以SM3算法常采用三段式,分为初始化(emit)、多次更新(update)、结束(final)。解释由于算法无法事先知道消息长度差额,所以消息填充要放在final阶段。还提及我国商密标准GMT0018中规定的哈希算法SM3也是三段式,并展示三段式测试情况及与open SSL对照情况。
00:18:01 引入H MAC概念
介绍我国商密标准中关于哈希算法SM3的三段式规定,引出H MAC概念。讲解H MAC是带密钥的杂凑函数,可用于消息认证,消息认证有消息认证码、消息加密、数字签名三种方法,H MAC是使用单向散列函数构造消息认证码的方法,介绍其提出时间、公布情况及广泛应用。
00:19:21 H MAC的构造与运算
说明H MAC可使用多种高强度单向散列函数构造,利用密钥和明文进行两轮核心运算,介绍运算步骤分为七步,涉及标准中定义的固定值ipad和opad 。讲解实现方式也是三段式,并展示测试情况及与open SSL对照情况,最后结束本次关于杂凑函数的讲解。
✨ 内容亮点
- 实用要点:
- 设计实用单向函数时,要均衡考虑计算性能和破解强度。
- 为降低杂凑值碰撞概率,可适当增加杂凑值长度,但要平衡其与计算性能的关系,如常用256位杂凑值。
- 提高杂凑函数质量,使其生成均匀分布的杂凑值,可降低碰撞发生概率。
- 避免使用单向杂凑函数处理包含机密信息和公开数据的信息,以防长度延申攻击,建议使用消息验证码等算法。
- SM3算法实现时,一段式要与open SSL对照验证;三段式要注意消息填充在final阶段进行。
- 精彩观点:
- 用打碎盘子易恢复难类比单向函数正向易逆向难的特性,形象生动。
- 指出密码杂凑算法需具备雪崩效应,即输入微小变化导致输出巨大变化,以SM3计算两个仅一比特不同字符串展示该效应,直观体现其重要性。
- 说明H MAC作为使用单向散列函数构造消息认证码的方法,在众多密码协议中广泛应用,成为事实上的网络安全标准,强调其重要地位。
- 工具资源:
- open SSL:可用于辅助验证SM3算法一段式和三段式实现的正确性,将自己编写程序的计算结果与之对照。
- 行动建议:
- 在设计单向函数时,依据实际需求,合理权衡计算性能与破解强度,选择合适的杂凑函数及杂凑值长度。
- 实现SM3算法时,按照标准实现一段式后,务必与open SSL对照验证结果。采用三段式实现时,严格将消息填充放在final阶段。
- 进行消息认证时,可考虑使用H MAC这种基于单向散列函数构造消息认证码的方法,并按照其七步运算步骤及三段式实现方式进行操作,同时与open SSL对照测试。
2、补充说明
1. 单向函数 (One-Way Function)
- 难点:“正向容易,逆向困难”这个性质为何如此重要?
- 补充说明: 这确保了不可逆性。在密码学中,哈希函数的核心用途之一就是存储密码。系统存储的是密码的哈希值,而不是明文密码。当您登录时,系统对您输入的密码再次进行哈希运算,然后与存储的哈希值对比。因为哈希函数不可逆,即使数据库泄露,攻击者也无法直接获得用户的明文密码(但可以通过彩虹表等方式攻击弱密码,这就需要“加盐”)。 这种性质也是数字签名的基础。签名是对信息的哈希值进行加密,验证时重新计算哈希并解密签名对比。不可逆性保证了无法从签名或哈希值反推出原始信息。
2. 杂凑值碰撞 (Collision)
- 难点:为什么不可避免?增加长度为何能降低概率?
- 补充说明: 鸽巢原理:这是一个非常直观的数学原理。假设有10个鸽巢(哈希值)和11只鸽子(输入信息),无论怎么分配,至少有一个鸽巢里会有两只以上的鸽子。这就是碰撞。哈希函数将无限可能的输入映射到有限的固定长度输出上,碰撞是必然存在的。 生日攻击:找到碰撞的难度远低于你的直觉。对于一个
n位的哈希值,你不需要尝试2^n次才能找到碰撞,平均只需要大约2^(n/2)次。这就是为什么256位哈希(n=256)的抗碰撞安全强度是2^128,而不是2^256。增加输出长度n会以指数级增长2^(n/2),从而使找到碰撞的难度变得巨大。
3. MD结构 (Merkle-Damgård Structure)
- 难点:迭代压缩的过程具体是怎样的?
- 补充说明: 可以把MD结构想象成一个多轮的搅拌机: 预处理(填充):将原始消息(比如一杯水果)切块、填充,使其长度刚好是搅拌杯(512bit)的整数倍。 初始化:设置一个初始的“底料”(Initialization Vector, IV)。 迭代压缩: 将第一块水果(第一个512bit分组)和底料(IV)一起放入搅拌机(压缩函数CF)中搅拌。 搅拌后得到一杯新的、混合均匀的果泥(中间哈希值
Hi)。 将这杯果泥作为新的“底料”,再加入下一块水果(下一个分组)继续搅拌。 如此重复,直到所有水果块都搅拌完毕。 输出:最后一轮搅拌出的果泥(最终哈希值Hn)就是这杯水果的唯一数字指纹(256bit的杂凑值)。 为什么这么设计? 这种结构允许我们对流式数据或超大文件进行哈希计算,而无需将整个文件同时加载到内存中。每次只处理一个分组,极大地节省了内存。
4. 数据填充 (Padding)
- 难点:填充规则为什么这么复杂?
k个0是怎么算出来的? - 补充说明: 目的1:对齐:确保总长度是512bit的倍数,以便分组。 目的2:防止攻击:包含原始长度信息(最后64位)可以有效防御长度扩展攻击。没有这个,攻击者可以在不知道原始消息的情况下,在哈希值后追加新的数据并计算出合法的哈希值。 计算
k:规则是(L + 1 + k) ≡ 448 (mod 512)。L是原始消息的比特长度。+1是代表先添加的那个比特1。 我们要让整个消息(原始消息 +1+k个0)的长度刚好比512的整数倍少64位(因为最后还要加64位的长度信息)。 所以,(原始消息长度 + 1 + k) = 512*N - 64,其中N是某个整数。移项后就是L + 1 + k + 64 = 512*N,即L + 1 + k ≡ 448 (mod 512)。k就是满足这个等式的最小非负整数。
5. 三段式实现 (Init/Update/Final)
- 难点:为什么需要三段式?和一段式有什么区别?
- 补充说明: 一段式:适用于已知整个消息内容且可以全部加载到内存中的场景。例如,计算一个文件的哈希值,文件大小只有几MB。函数调用:
hash = sm3_once(entire_message)。 三段式:适用于未知长度或超大的数据流。Init(ctx): 初始化一个上下文结构体ctx,里面保存了中间状态(IV,已处理的数据长度等)。Update(ctx, part_of_message): 传入上下文和一部分消息。函数内部会处理能处理的分组,并更新上下文状态。你可以多次调用Update。Final(ctx, hash): 当所有数据都通过Update送入后,调用此函数。它负责进行最后的填充工作,处理最后一个分组,并输出最终的哈希值。 关键点:在Final被调用之前,算法是不知道消息的总长度的,因此无法完成填充。这就是为什么填充必须在Final阶段进行。这种设计非常灵活,可以用于计算网络数据流、实时传感器数据或超大文件的哈希。
6. HMAC (Hash-based Message Authentication Code)
- 难点:已经有了哈希,为什么还需要HMAC?
ipad和opad是干什么的? - 补充说明: 目的:消息认证。确保消息不仅完整,而且来自正确的、拥有共享密钥的发送方。防止攻击者同时篡改消息和哈希值。 工作原理:HMAC巧妙地将密钥与消息混合后进行两次哈希运算。 将密钥处理成与分组长度相同(如512bit)的块。 将处理后的密钥与一个固定的常量
ipad(inner pad)进行异或操作。 将上一步的结果放在消息前面,整体做一次哈希,得到一个中间结果。 再将处理后的密钥与另一个固定的常量opad(outer pad)进行异或操作。 将第4步的结果放在第3步的中间结果前面,再做一次哈希,得到最终的HMAC值。ipad和opad的作用:它们是两个不同的常量(0x36和0x5C),目的是让两次哈希运算的输入有根本性的差异,从而确保即使密钥处理后有某种特性,经过两次不同的混合和哈希后,最终结果也是安全的。这种结构被严格证明其安全性与底层哈希函数的安全性相关。
7. 我的贡献
倾听课程,梳理主要内容,标记不太懂的地方,然后对照GET笔记整理的内容总结,明确自己不理解或有困惑的地方,再和AI沟通交流,最后整理成文档。
3、编译运行相关代码,使用gdb运行相关代码
详细参见:https://www.cnblogs.com/eleslsel/p/19123034
SM3-一段式
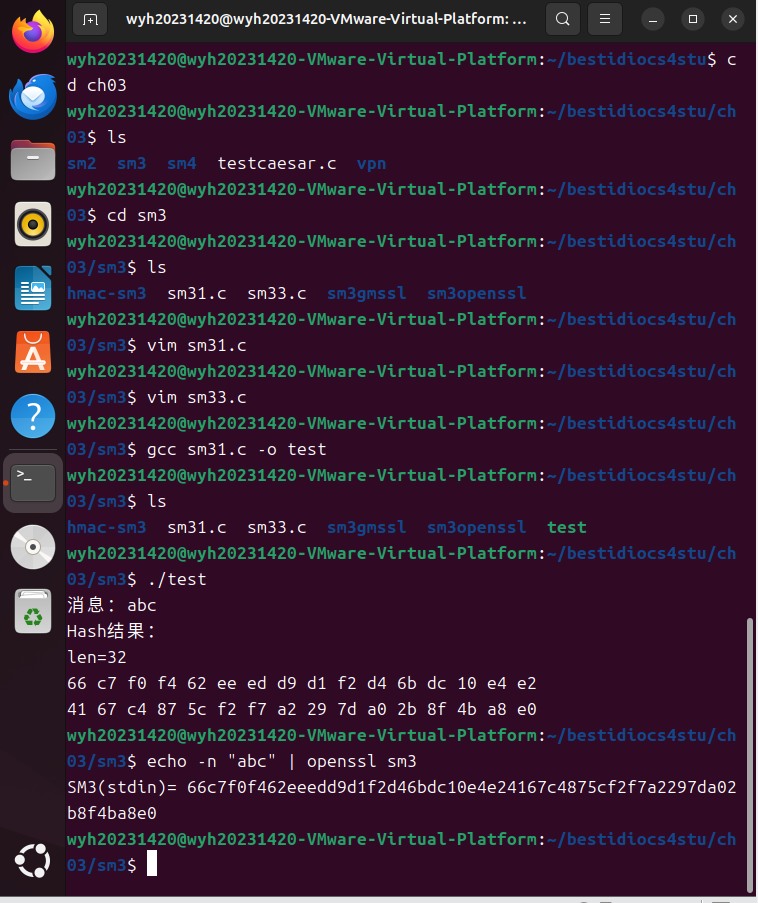
SM3-三段式
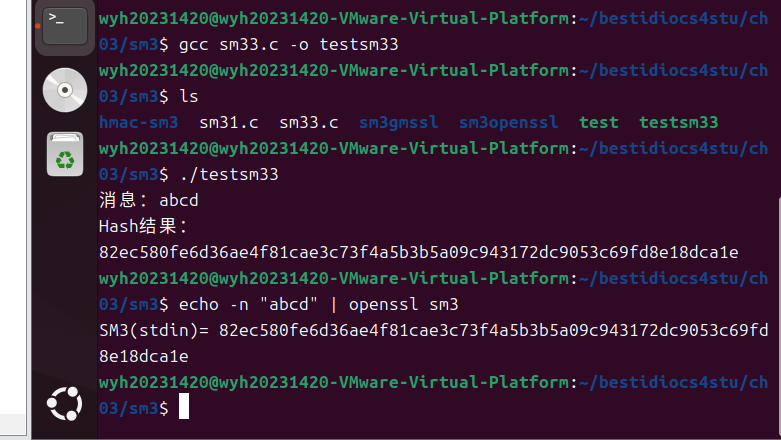
HMAC-sm3
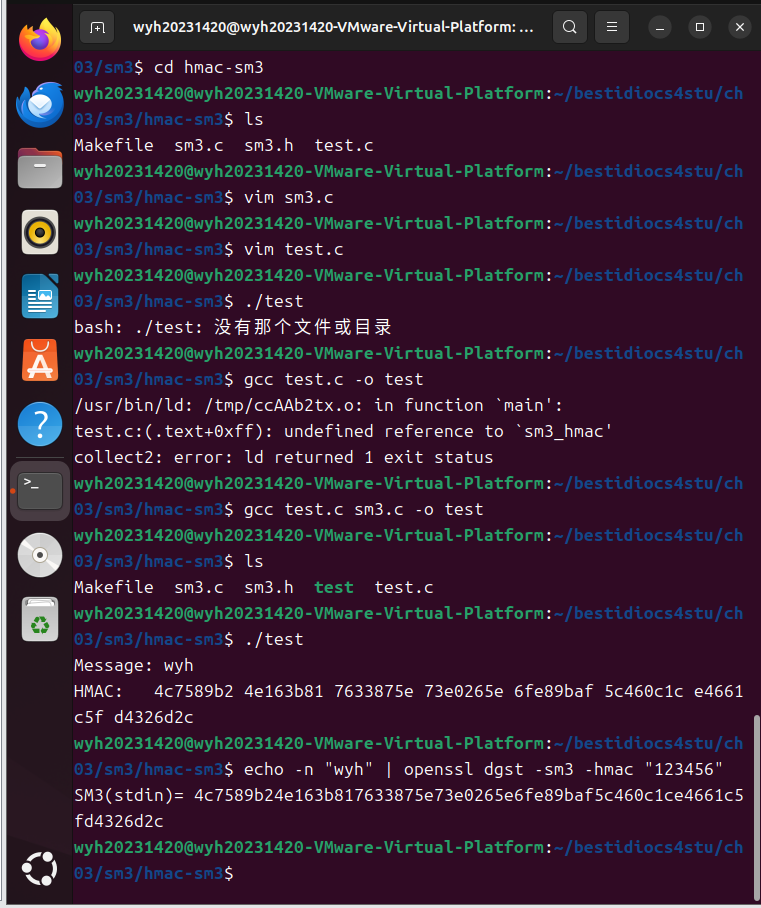




 浙公网安备 33010602011771号
浙公网安备 33010602011771号