红黑树和b+树

二叉搜索树

满足以下条件：

1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1.
   

这是一个正常的，没有碰到极端情况的二叉搜索树。

如果数据是有序的或者在删除，插入操作下，那么可能会退化成一条链。严重影响性能。

平衡二叉搜索树（AVL）

在这种情况下可以通过不同的旋转操作来保证树的平衡。

• “节点高度”是指从该节点到它的最远叶节点的距离，即所经过的“边”的数量。
• 节点的平衡因子（balance factor）定义为节点左子树的高度减去右子树的高度，同时规定空节点的平衡因子为 0 。
• 我们将平衡因子绝对值 >1 的节点称为“失衡节点”

旋转

旋转操作是为了将二叉树重新平衡。
在插入或删除的时候，如果节点失衡，平衡因子的绝对值只能是2。

5 和 7 是失衡节点。它们失衡是因为 1 的存在，从节点 5 到 1 有两条边，这是罪魁祸首，只要把 3 作为 1 ，5 的父节点就好了。

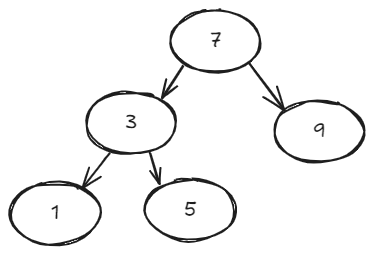
但是为什么不把 5 作为 3 ，7 的父节点呢？找离新插入的节点最近的不平衡的树进行调整
为什么要这么操作呢？

• AVL树的平衡性是递归定义的。每个节点的左右子树高度差不能超过1。

• 如果只调整离新插入节点最近的不平衡节点，可以确保该节点的子树恢复平衡，同时更高层的节点也会因为子树高度的调整而自动满足平衡条件。

• 如果跳过最近的不平衡节点，直接调整更高层的节点，可能会导致低层节点再次失衡，从而需要额外的调整。
  对于其它的旋转操作来说，都是为了保证 AVL 树的性质不变。

红黑树

• 特性1：节点非黑即红

• 特性2：根节点一定是黑色

• 特性3：叶子节点（NIL）一定是黑色

• 特性4：每个红色节点的两个子节点都为黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

• 特性5：从任一节点到其每个叶子的所有路径，都包含相同数目的黑色节点。
  从以上性质可以知道左右子树的高度差最大的时候是黑红相间，这样的规定使得调整平衡的操作相对于 AVL 比较少。

插入

• 规定插入的节点是红节点，如果是黑节点一定破坏了 特性5，而红节点有可能破坏 特性4.

叔叔为红

只好将 7 变红，3 ，9 变黑，同时将注意力放到 7 上递归向上。

叔叔为黑

只需要保证这棵子树的父节点为黑，并满足上述性质。
将 3 变黑，通过旋转，变为父节点，7 变红。

删除

• 如果是红色节点没有任何问题直接删除，如果是黑色节点则必定会违反 特性5.
  如果删除后，将兄弟子树也去掉一个黑色节点，就要将注意力转移到它们的父节点上，递归向上。
  
  删掉 9 将 3 变红，压力给到 7.
  如果要保持黑节点不变，就要旋转加变色，来保证红黑树的性质。

B树

可以知道的是上述 AVL 树和红黑树的高度较高，如果数据量较大的情况下，数据在硬盘上，访问一个节点时要进行一次硬盘操作。树高度和访问硬盘的操作正相关。所以我们要压缩树的高度，增加每个节点数据量。

• 平衡：所有叶节点都在同一层。
• 有序：节点内有序，任意元素的左子树小于它，右子树大于它。
• 对于m阶B树，节点最多有m个分支，m-1个元素。对于根节点，最少2个分支，一个元素，非根 $[m/2]$ 个分支，$[m/2] -1$个元素。
  
  B树的插入删除操作和二叉搜索树的相似同时要满足节点最少和节点最大的条件，就不过多讨论。

B+树

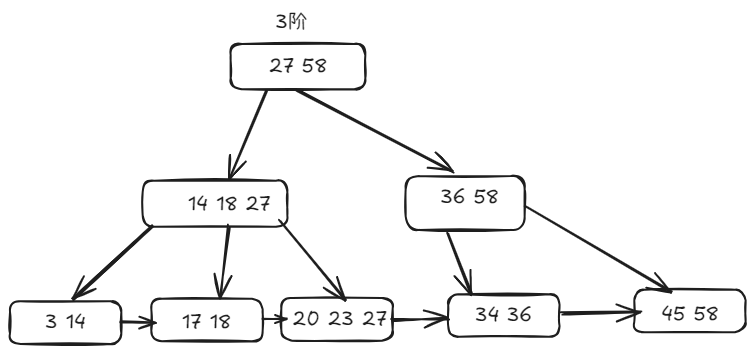
• 与B树的不同：对于m阶B树，节点最多有m个分支，m个元素。对于根节点，最少2个分支，两个个元素，非根 $[m/2]$ 个分支，$[m/2]$个元素。
  
  B树在顺序遍历的时候只能中序遍历，远没有B+树链式遍历的快。同样的 B+树也可以很方便的进行随机查找。