构建最小平均查找次数二叉搜索树 OBST问题
OBST 经典问题
问题描述
问题:现有 n 个节点,其值从大到小为 \(a_{1}, a_{2}, ... ,a_{n}\), 对应的每个节点查找概率为 \(p_{1}, p_{2}, ... , p_{n}\)。试求出一种二叉搜索树,可以使得平均查找次数最小。
解决思路
首先我们要理解如何计算查找一个值的查找次数,假设存在这样一个二叉搜索树: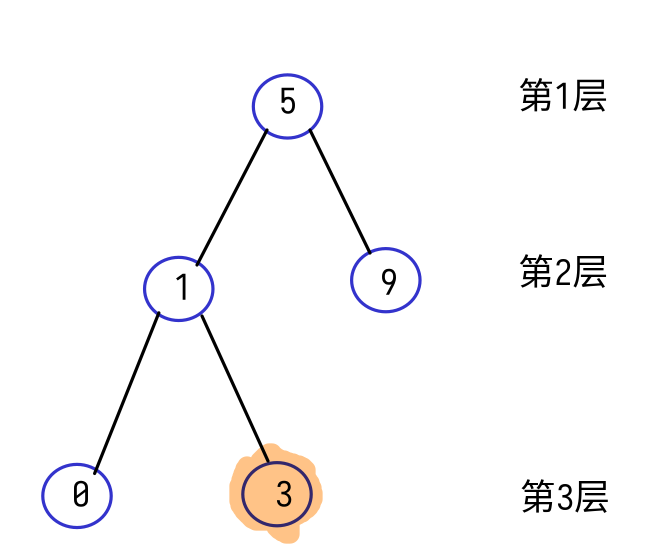
那么当搜索的值为 3 时,其查找次数是三次:
- 先检查根节点是否等于 3,显然 3 < 5, 所以递归到左子树继续查找
- 再检查新的节点是否等于 3, 显然 3 > 1,所以要继续查找右子树
- 最后找到 3
因此可以发现,无论是最好还是最坏情况,查找一个值所需要的比较次数都是其所在的层数,即:$$c_{i}=r_{i}$$
那么该点的期望查找次数就根据期望公式 \(E(i) = p_{i}\times c_{i}\) ,也就是该点的预期查找成本。
一般来说,关于从一个数组到树的构建问题可以从动态规划的角度来考虑,且尤其属于区间DP。
对于该题,首先根据动态规划的基本思想尝试划分子问题:
- 对于 \(a_{1}, a_{2}, ... ,a_{n}\) ,我们可以通过选中一个节点作为原始根节点,将问题划分为两部分
- 构建左子树的最优BST(包含节点 \(i\) 到 \(k−1\))
- 构建右子树的最优BST(包含节点 \(k+1\) 到 \(j\)),其中 \(k\) 是选为根的节点。
- 而在非常多的划分情况中,很多子问题会重复出现,即我们可能会多次计算 \(a_{1},a_{2},a_{3}\) 所构成的子树
- 因此,我们可以在枚举划分方法的同时,记录每次计算的子问题值,从而在继续枚举的过程中,不必重新计算一次而优化时间复杂度(这也是动态规划的核心特点)
进一步思考,我们得出的子问题划分方式可以总结为:$$f(i,j)=\min{{f(i,k-1)+f(k+1,j)}} + c_k$$
即构建在 \([i,j]\) 区间中的二叉搜索树时的平均查找时间 \(f(i,j)\),其成本为 \(f(i,k-1)\) 和 \(f(k+1, j)\) 两个子问题的内部最优成本, 以及加上 \(k\) 节点作为根 节点后, \([i,k-1]\) 和 \([k+1,j]\) 之间的节点因为新增的深度而增加的成本,还有 \(k\) 节点本身的成本。
可以发现实际上就是 \([i,j]\) 区间的概率和:$$c_{k}=\sum_{m=i}^{j}\limits{p_{m}}$$
因此状态转移公式为:$$f(i,j)=\min{{f(i,k-1)+f(k+1,j)}} + \sum_{m=i}^{j}\limits{p_{m}}$$
当 \(i=j\) 时,只有一个点,所以其最优情况就是本身作为根节点,即 $$f(i,i)=p_{i}$$
C++代码
至此,可以得出一份C++代码来解决这个问题:
#include <iostream>
using namespace std;
const int N = 10;
double optimalBST(double p[], int n)
{
double dp[N][N]; // dp[i][j]表示从i到j的最优解,和PPT中的 C(i,j) 相对应
// 初始化
for (int i = 0; i < n; i++)
dp[i][i] = p[i];
// 从长度为2的子序列开始递推
for (int len = 2; len <= n; len++)
{
for (int i = 0; i + len - 1 < n; i++)
{
int j = i + len - 1; // [i,j] 是长度为 len 的区间
dp[i][j] = 1e9;
double sum = 0; // 对应公式中的 C_k
for (int k = i; k <= j; k++)
sum += p[k];
for (int k = i; k <= j; k++)
{
double left = k - 1 >= i ? dp[i][k - 1] : 0;
double right = k + 1 <= j ? dp[k + 1][j] : 0;
dp[i][j] = min(dp[i][j], left + right + sum);
}
}
}
return dp[0][n - 1]; // 最后返回 dp[0][n - 1],表示原本 p 的最优解
}
int main()
{
double p[4] = {0.1, 0.2, 0.4, 0.3};
double res = optimalBST(p, 4);
printf("%f\n", res);
return 0;
}
填表法
若要手动计算,即PPT上的填表法,则也是先进行初始化 \(i=j\) 时候的值为原概率:
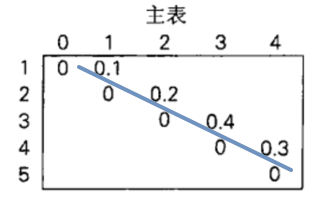
接着开始填下一个对角线,首先是 \((1,2)\) 区间,也就是 0.1 右边的点,根据公式:$$f(i,j)=\min{{f(i,k-1)+f(k+1,j)}} + \sum_{m=i}^{j}\limits{p_{m}}$$
所能取到的 \(k\) 值有两种情况, \(k=1,k=2\) ,因此分别带入计算,取最小值:
取最小值 \(0.4\) 也就是 \(k=2\) 的情况(意味着根节点取2号),所以计算得出 \(f(1,2) = 0.4\),填入 \((1,2)\) 位置即可。如法炮制就可以填满第二个正对角线的值:
继续填第三个对角线,对于 \((1,3)\) ,\(k\) 的取值有 3 种:
因此取最小值 \(1.1\),即根节点选 3 号的情况,此时我们就可以画出关于 \((1,3)\) 的最优查找次数的二叉搜索树,先选根节点为 3 号,剩余 1,2 号节点则根据 \(f(1,2)\) 的计算结果选择 2 号作为根: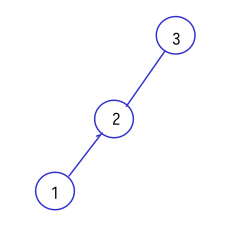
剩下依然如法炮制即可,得到的结果为: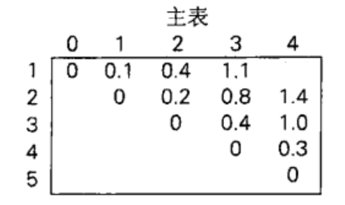
对于最后的 \((1,4)\) 也就是代表了整个问题的最终解的区间,\(k\) 的取值有4种:
最小值为 \(1.7\),即选择 3 号节点作为根节点的情况。至此,就可以画出整个数组所构建的最优二叉搜索树:
- 首先以 3 号点为根节点,分出来 \([1,2]\) 和 4 号节点
- 接着对于 \([1,2]\) 选择 2 号节点为根节点,分出来 \(1\) 号节点和空节点
所对应的图如下: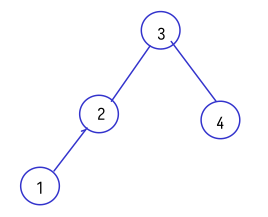
变体题目 P4539 [SCOI2006] zh_tree
问题:给你 n 个节点,每个节点对应的出现次数为 \(d_{i}\),设 \(S\) 是所有节点的出现次数,则每个点的出现频率(概率)为 \(p_{i}=\frac{d_{i}}{S}\) 。同时规定,若第 \(j\) 个节点的深度为 \(r\) , 则访问该节点的代价为 \(h_{j}=k(r+1) + c\) ,其中 \(k,c\) 为已知的不超过 100 的正整数。
构建一个最优搜索二叉树,使得 \(h_1p_1+h_2p_2+…+h_np_n\) 最小。
思路
和基本 OBST 问题不同的是,本题的代价不再单纯等于深度,并且根节点的深度为0。动态规划的基本特征肯定满足,依然是同样的划分方法:$$f(i,j)=\min{{f(i,k-1) + f(k+1,j)}}+c_{k}$$
对于 \(c_{k}\) ,它包含两个子树因增加1深度而增加的代价,以及根节点本身的代价,那么对于子树中的节点,深度+1,在公式\(h_{j}=k(r+1) +c\) 中就导致 \(h_{j}'=k(r+2) +c\),也就是说比之前多了一个 \(k\) 值。因此在计算过程中,不能像标准OBST问题一样仅仅乘上一个1就行,而是要乘上一个 \(k\) :
整理一下可得:$$c_{k}=k\sum_{m=i}^{j}\limits{p_{m}} + cp_{k}$$
剩余内容就和原本OBST问题一致。
代码
#include <bits/stdc++.h>
using namespace std;
/*
title: P4539 [SCOI2006] zh_tree
link: https://www.luogu.com.cn/problem/P4539
time: 2024年1月5日12:49:02
*/
const int N = 30;
int n;
double k, c;
double f[N][N];
double p[N];
void solve()
{
for (int i = 0; i < n; i++)
f[i][i] = (k + c) * p[i];
for (int len = 2; len <= n; len++)
{
for (int i = 0; i + len - 1 < n; i++)
{
int j = i + len - 1;
f[i][j] = 1e9;
double sum = 0;
for (int t = i; t <= j; t++)
sum += p[t];
for (int t = i; t <= j; t++)
{
double cost = sum * k + c * p[t];
f[i][j] = min(f[i][j], f[i][t - 1] + f[t + 1][j] + cost);
}
}
}
cout << setprecision(3) << fixed << f[0][n - 1] << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k >> c;
double S = 0;
for (int i = 0; i < n; i++)
{
cin >> p[i];
S += p[i];
}
for (int i = 0; i < n; i++)
p[i] /= S;
solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号