[Information Theory] L1: Introduction to Information Theory

http://www.inference.org.uk/mackay/itprnn/

 

http://videolectures.net/course_information_theory_pattern_recognition/

 

 

 

1948, Shanon's fundamental problem: Reliable communication over an unreliable channel

 

eg:

 

 

 

 

 

 

 

 

 

change the physics: replace equipment with a better one. 

system solution: add encoding and decoding 

 

 

 

 hat means a guess

 

s -> \hat{s}

 

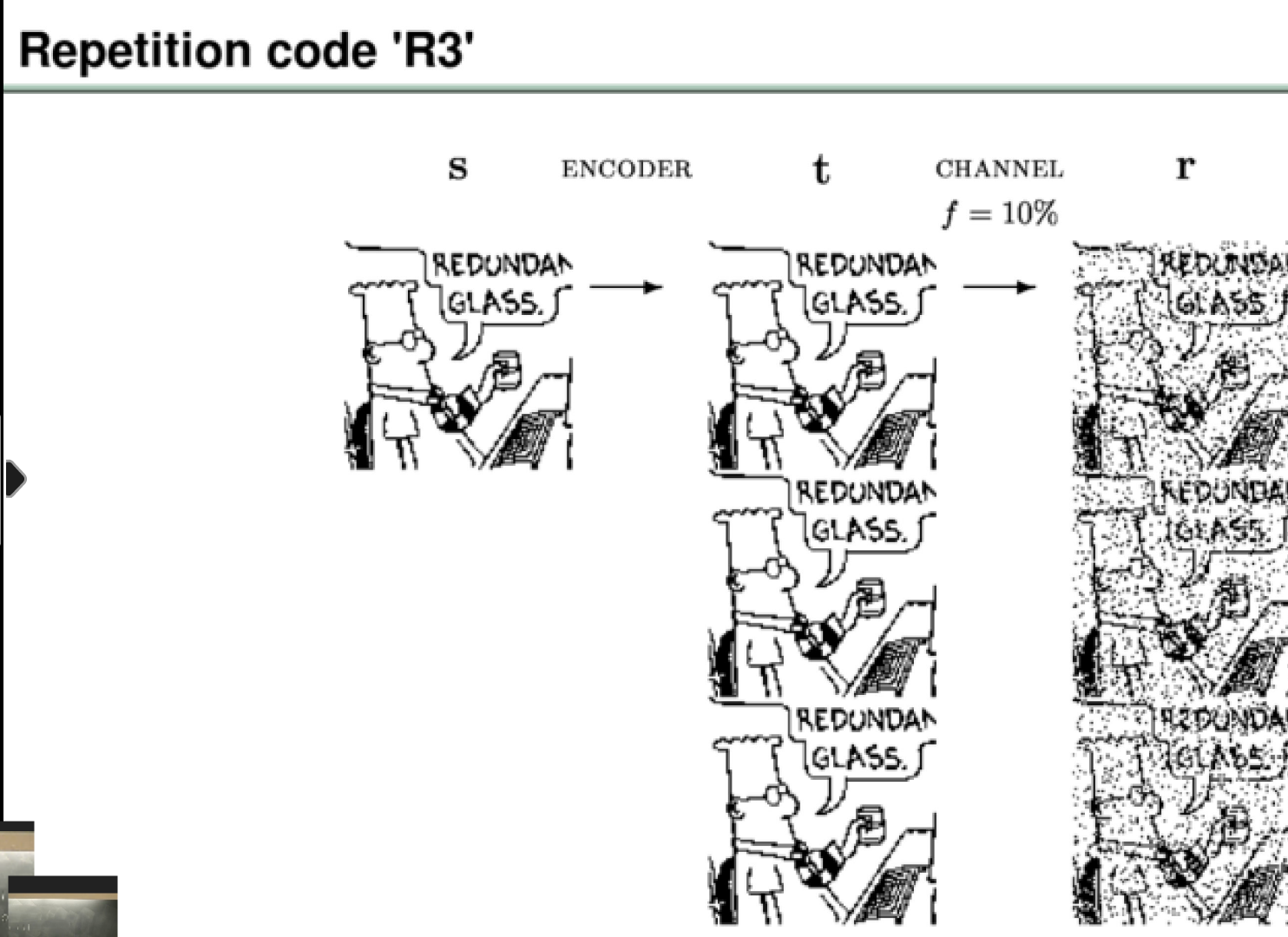
toy example: binary symmetric channel

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

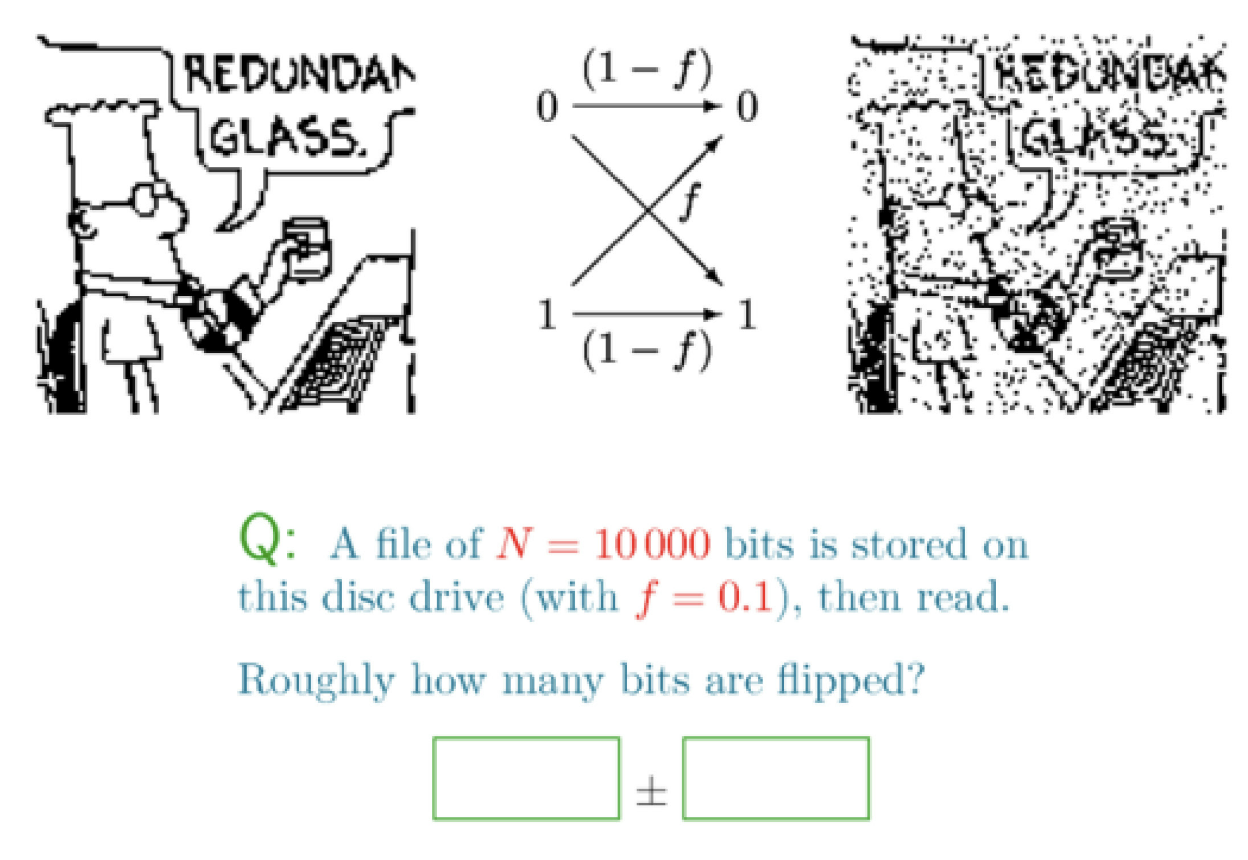
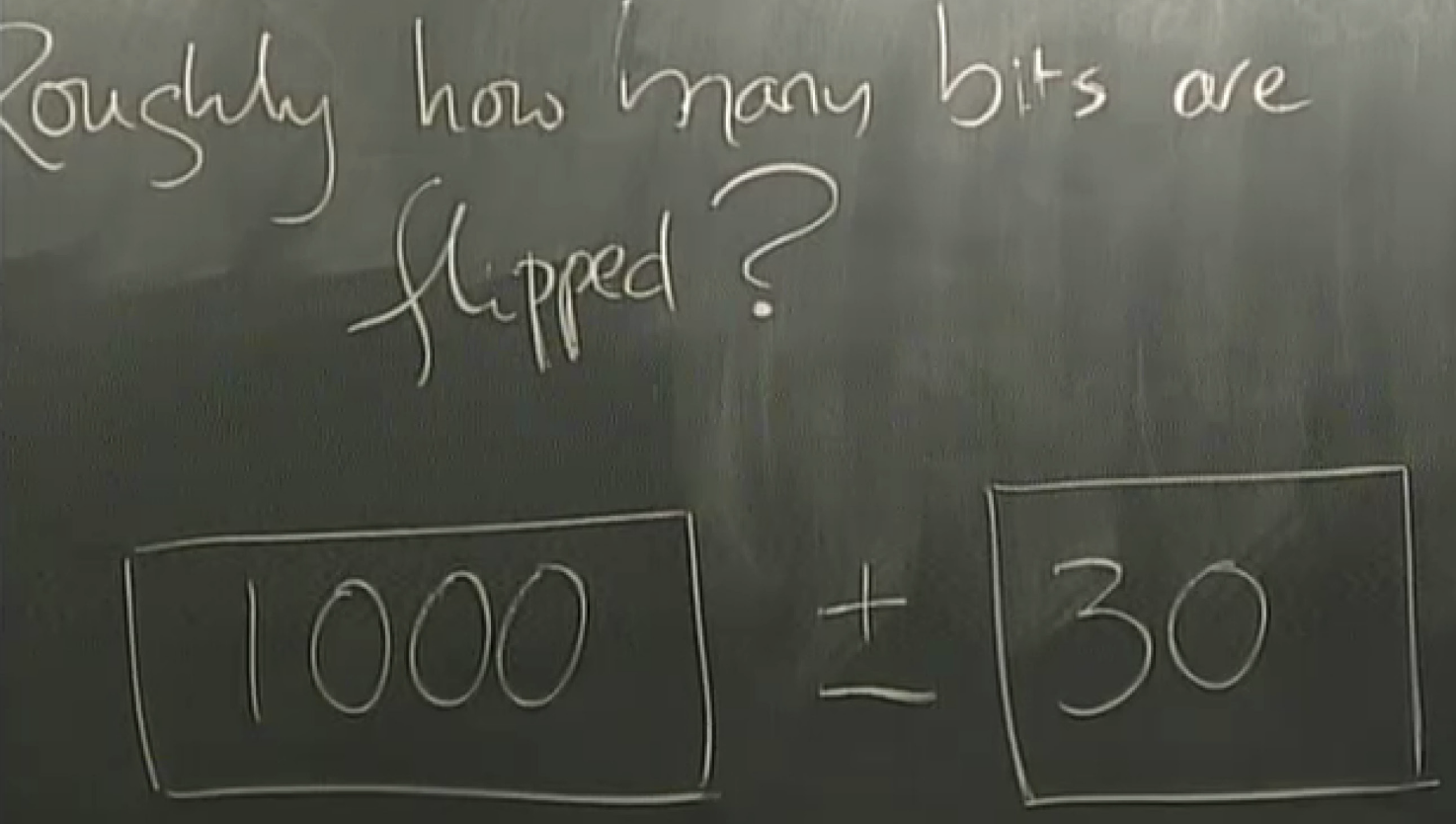
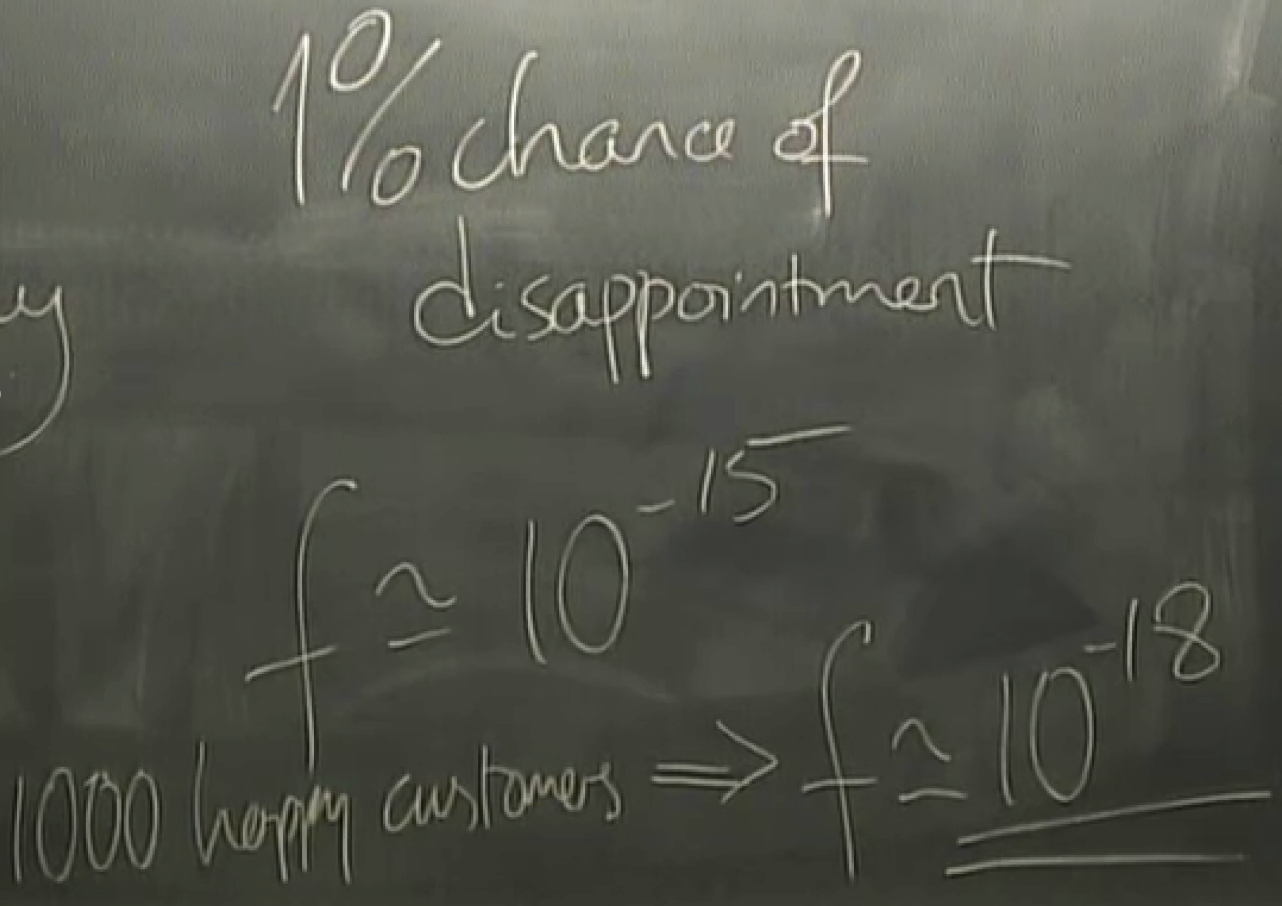
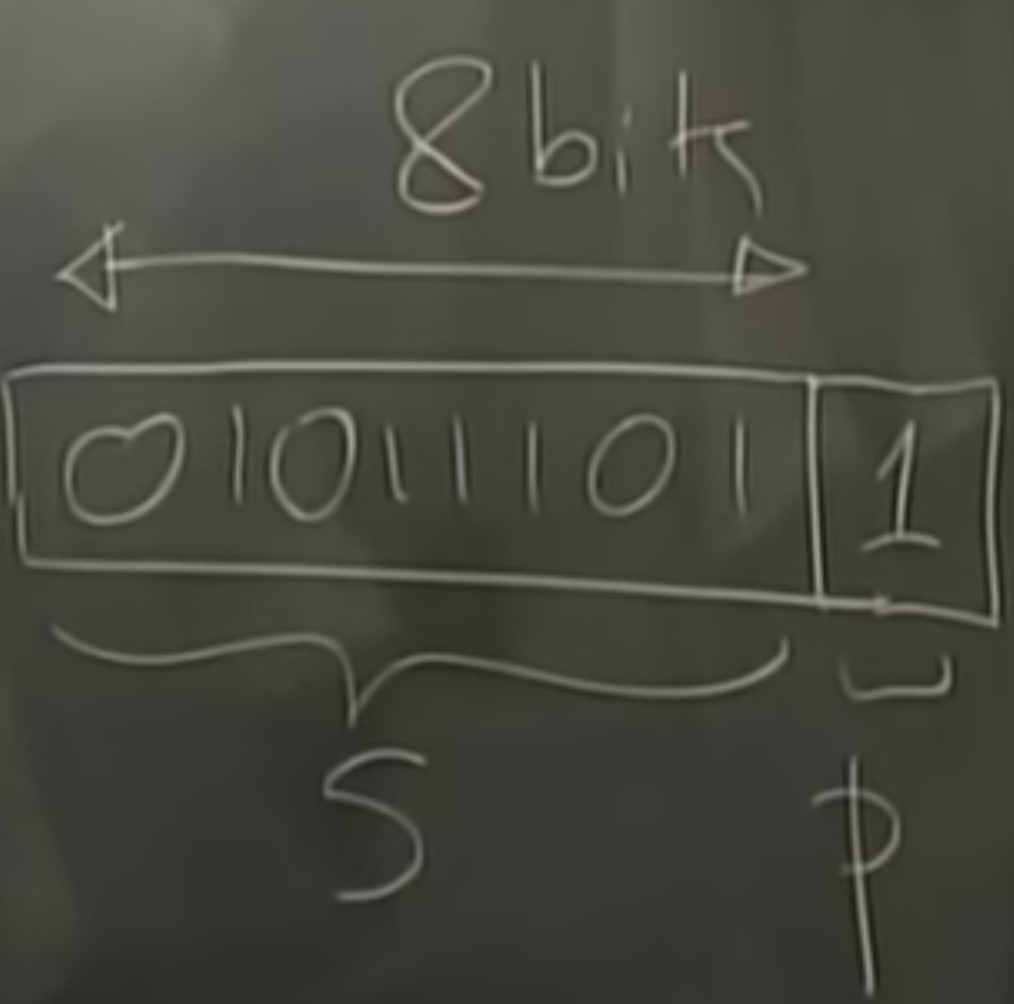
partity coding: even->0 for p; odd->1 for p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

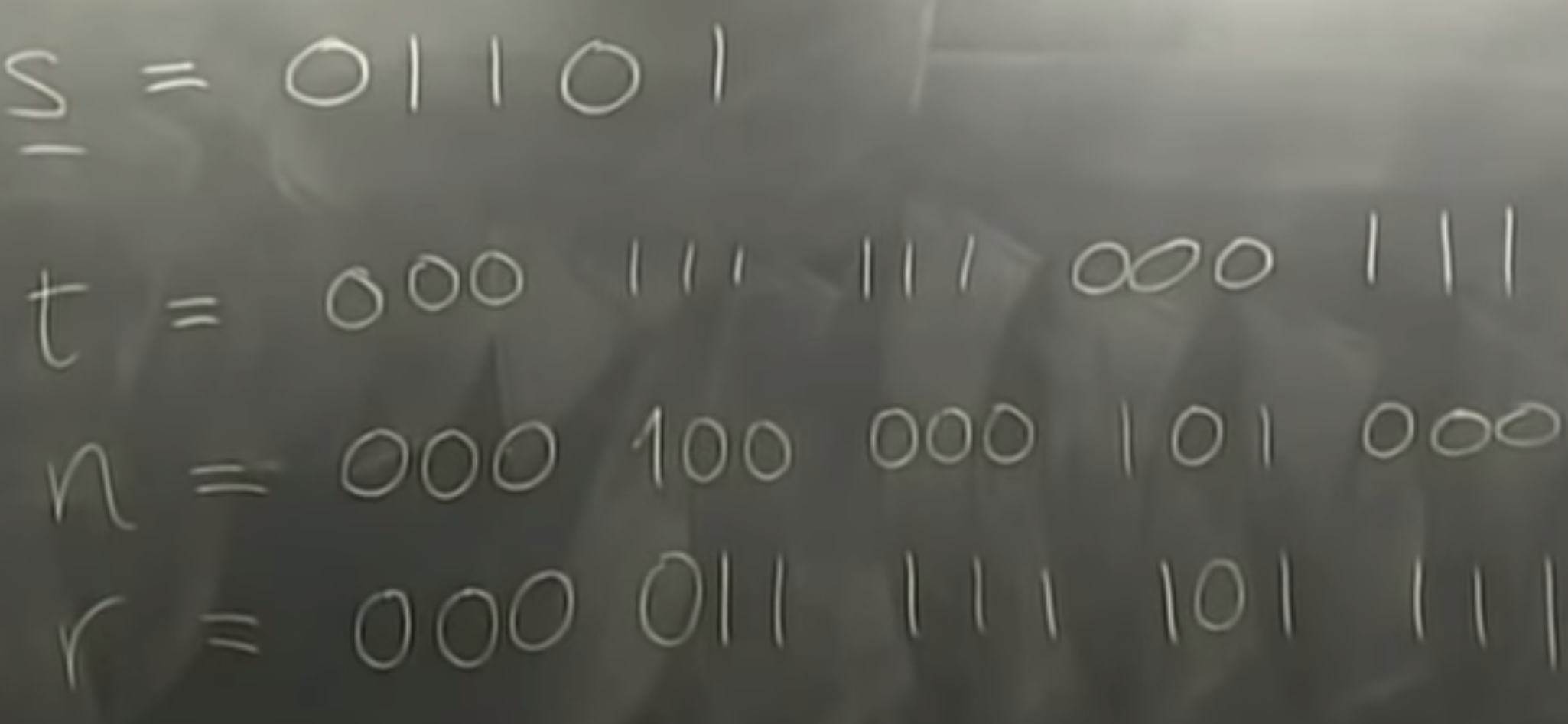
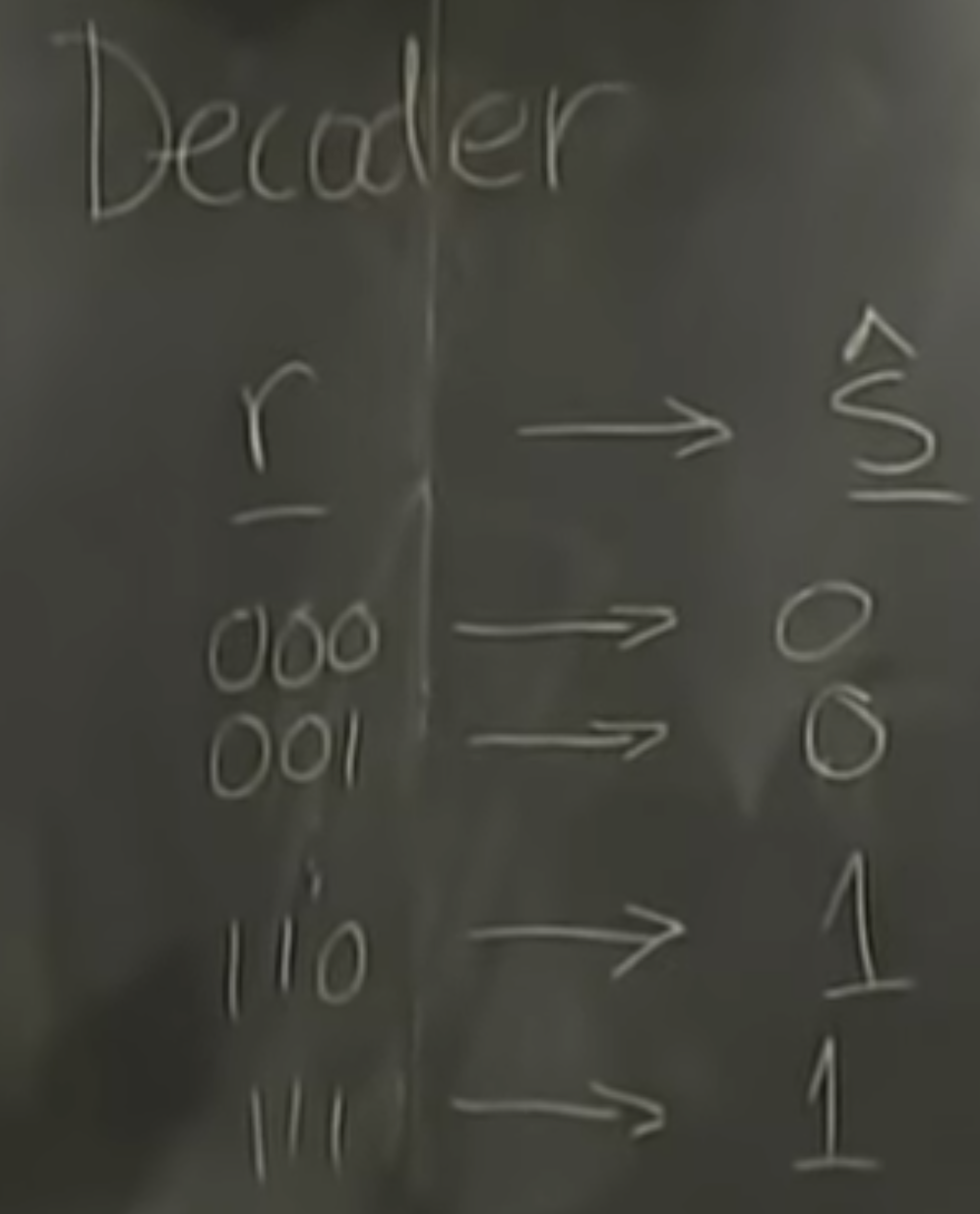
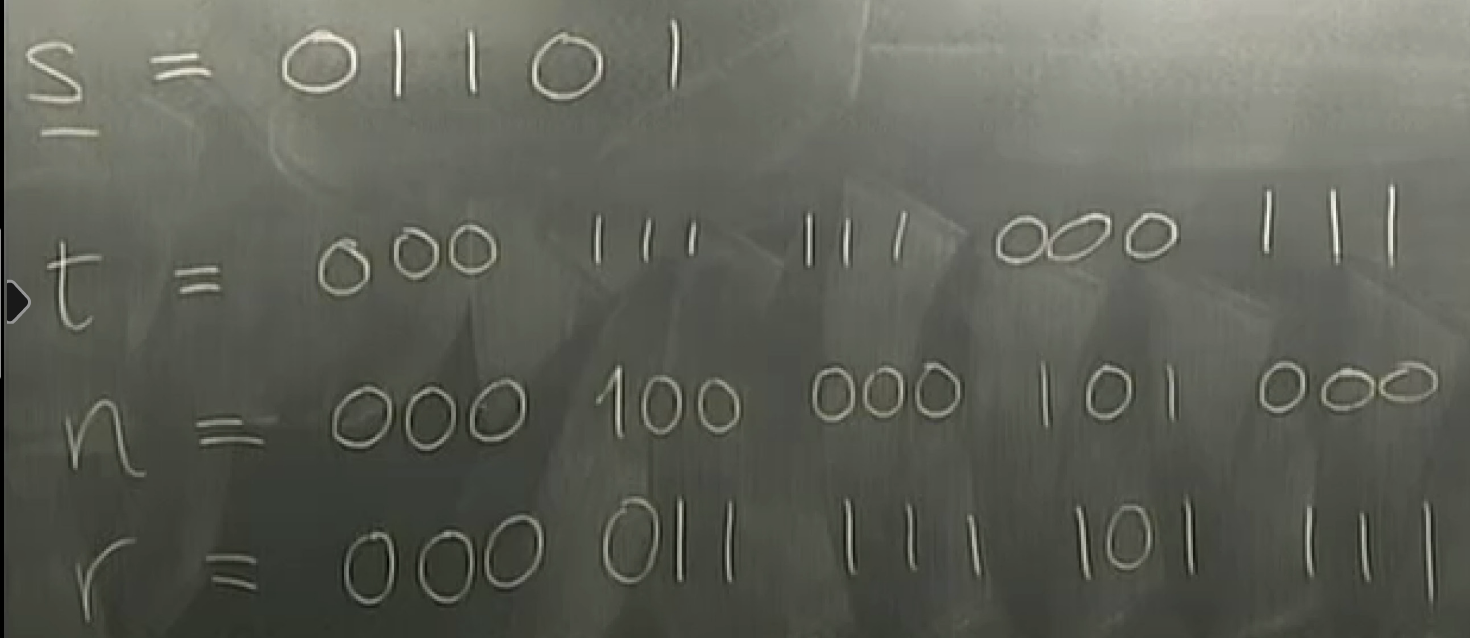
\hat{s} = 0 1 1 1 1

 

 

 

 

why the majority vote decoder is the best?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

 

 

 

 

 

 

 

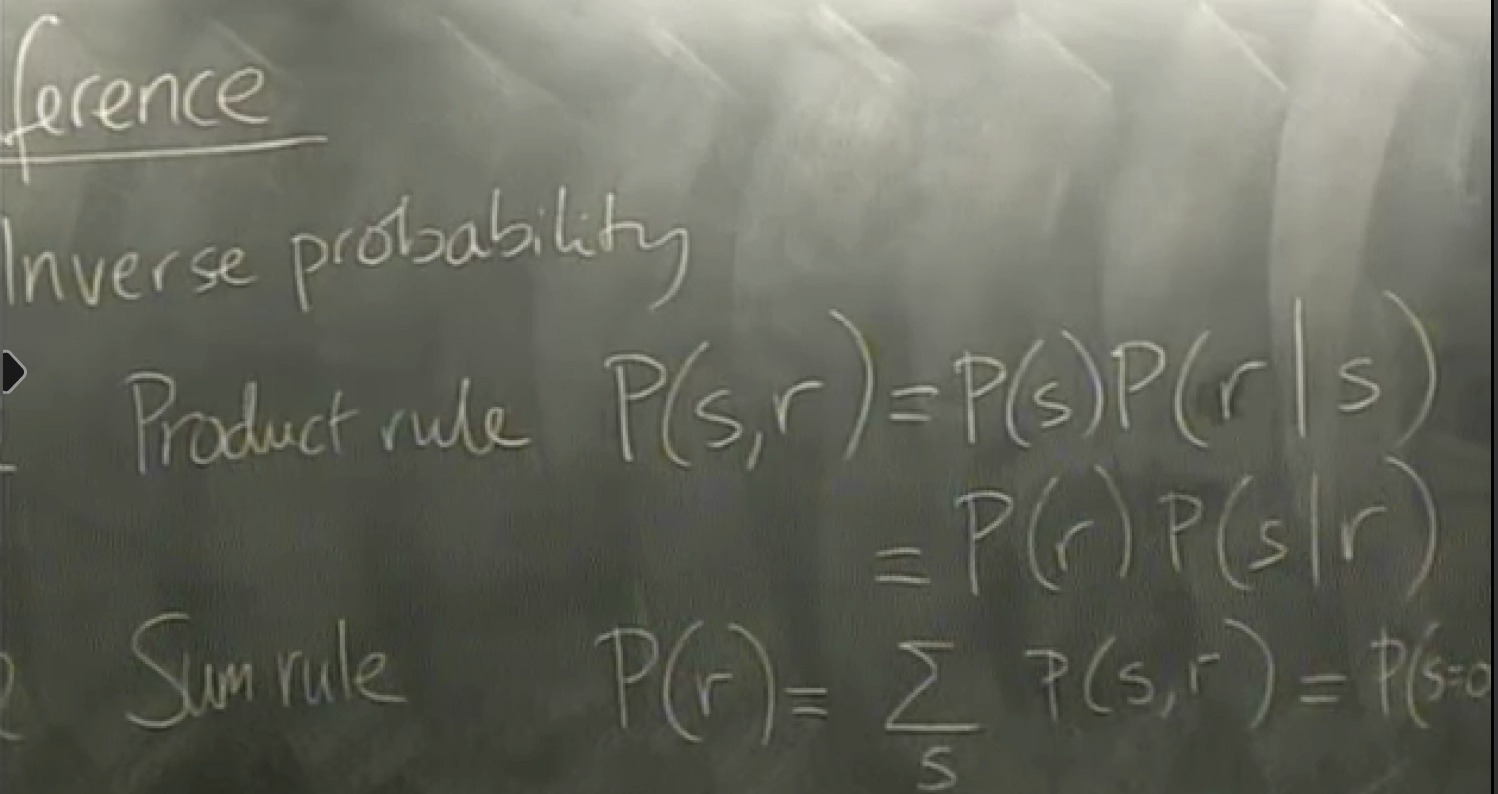
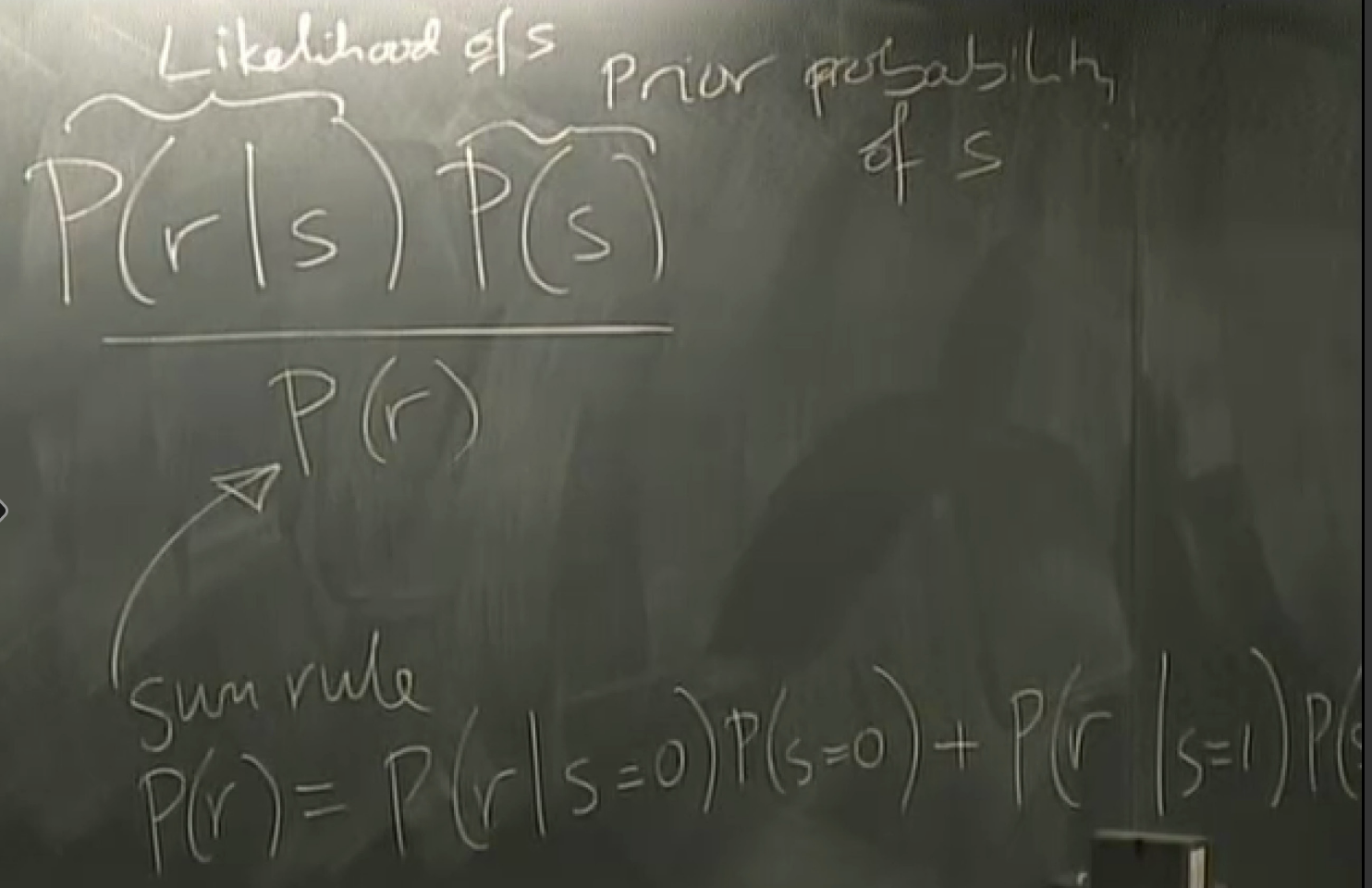
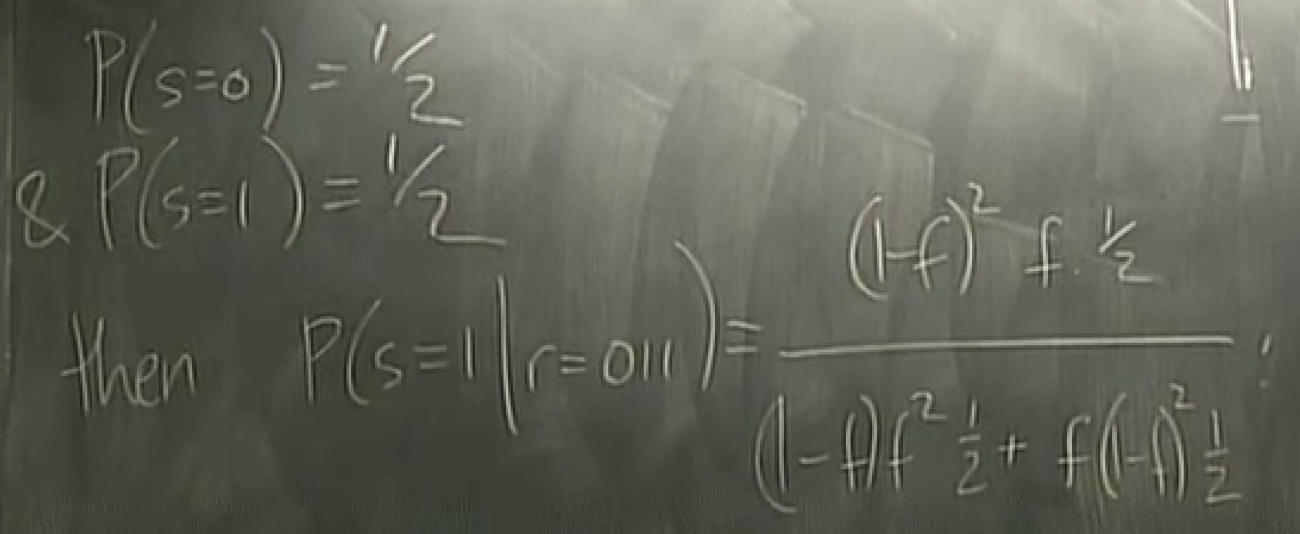
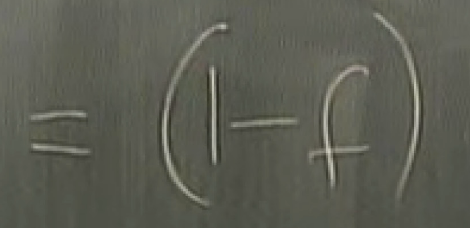
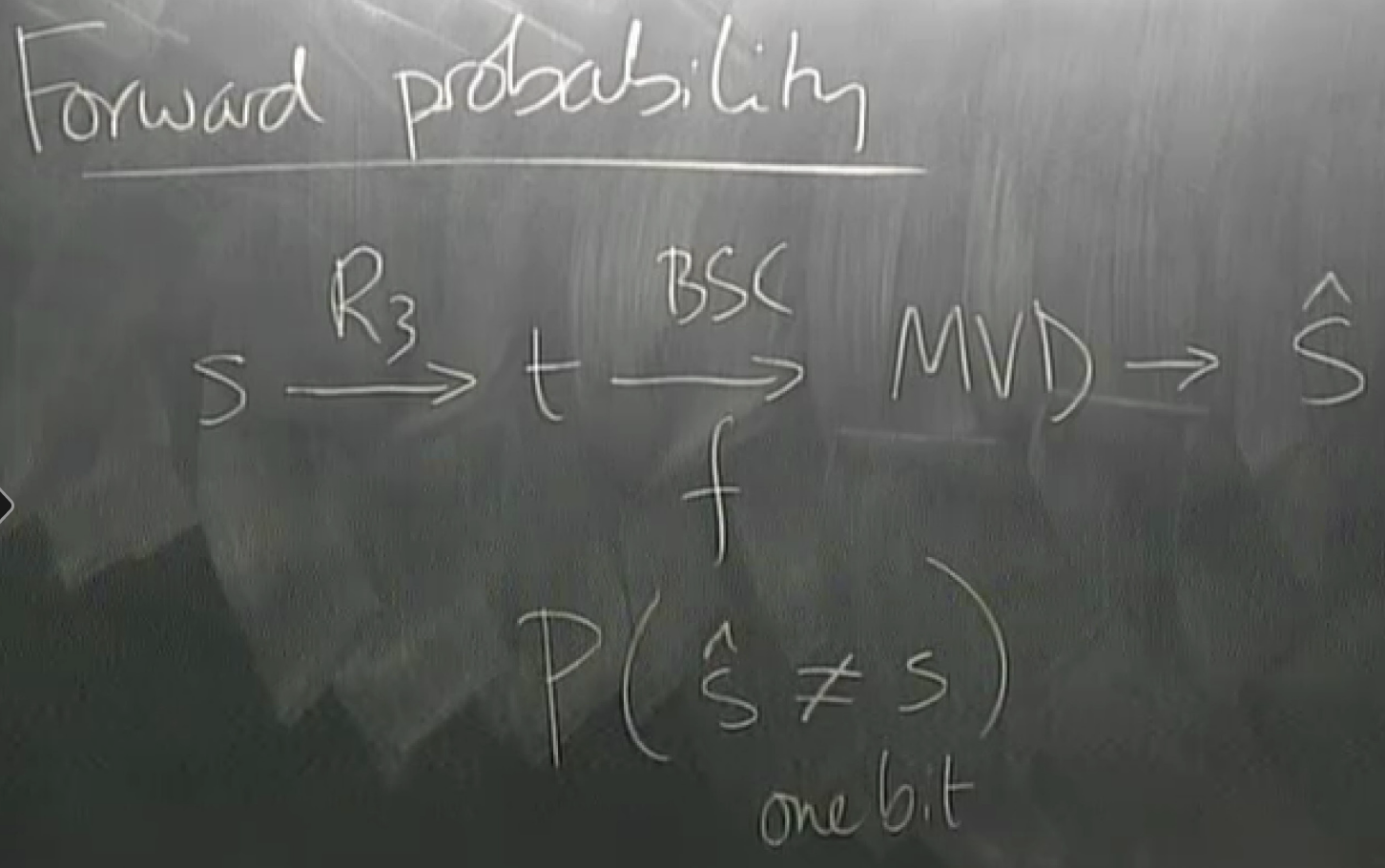
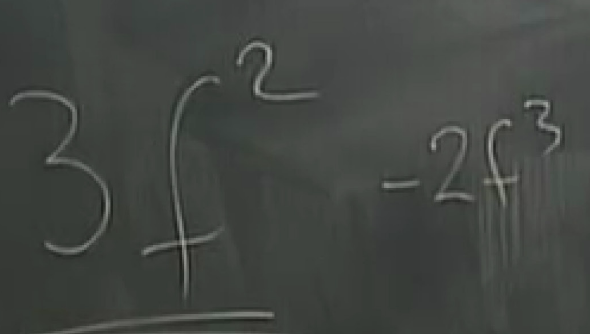
 answer: 61

 

 

 

 

74 hamming code

 

 

 

 

 

 

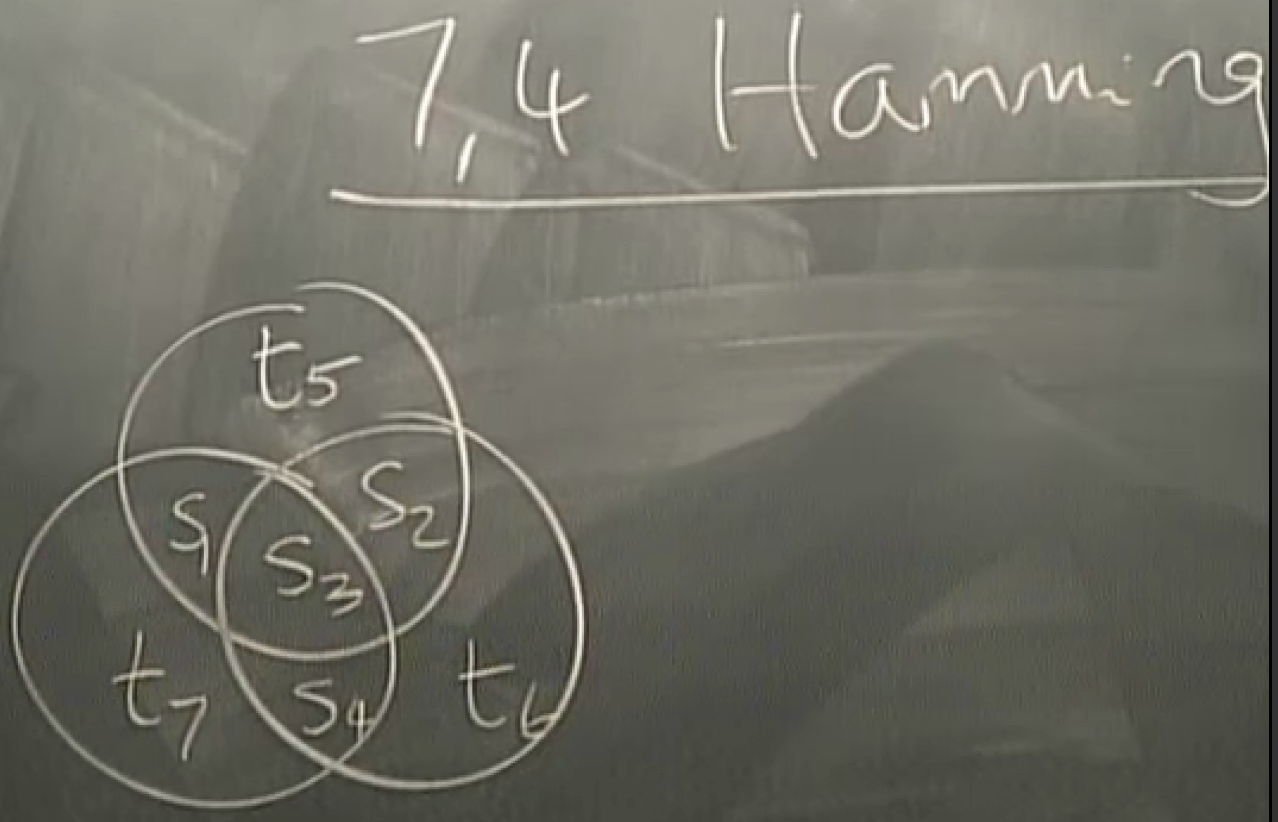
encoder: even for 0 and odd for 1

 

 

decoder:

 

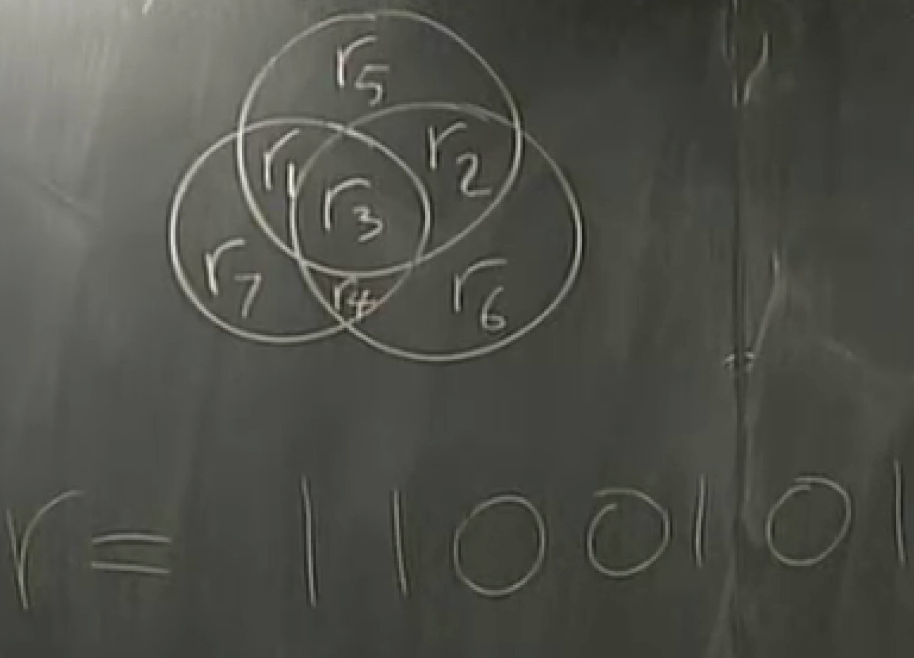
the second one got flipped but we dont know yet.

 

 

 

 

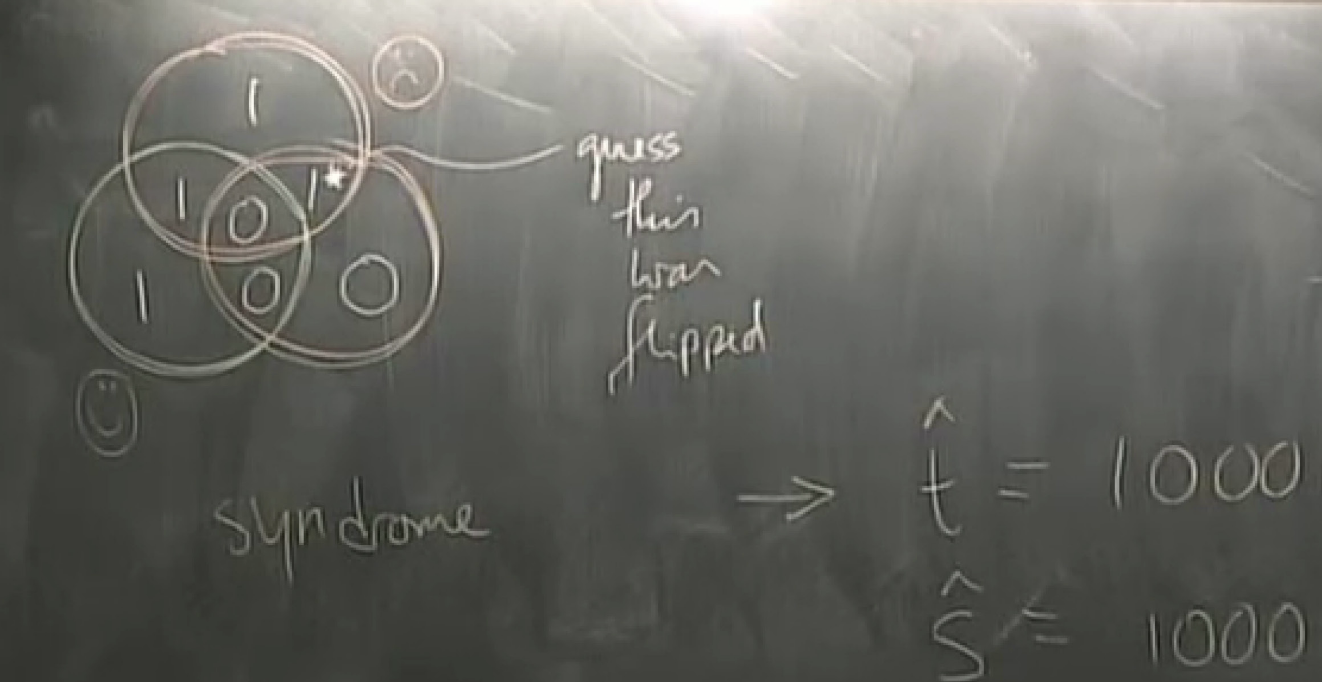
t = 1000101

 

any single flip can be detected and corrected, but if >1, then in trouble

 

 

 

 

 

 

 

 

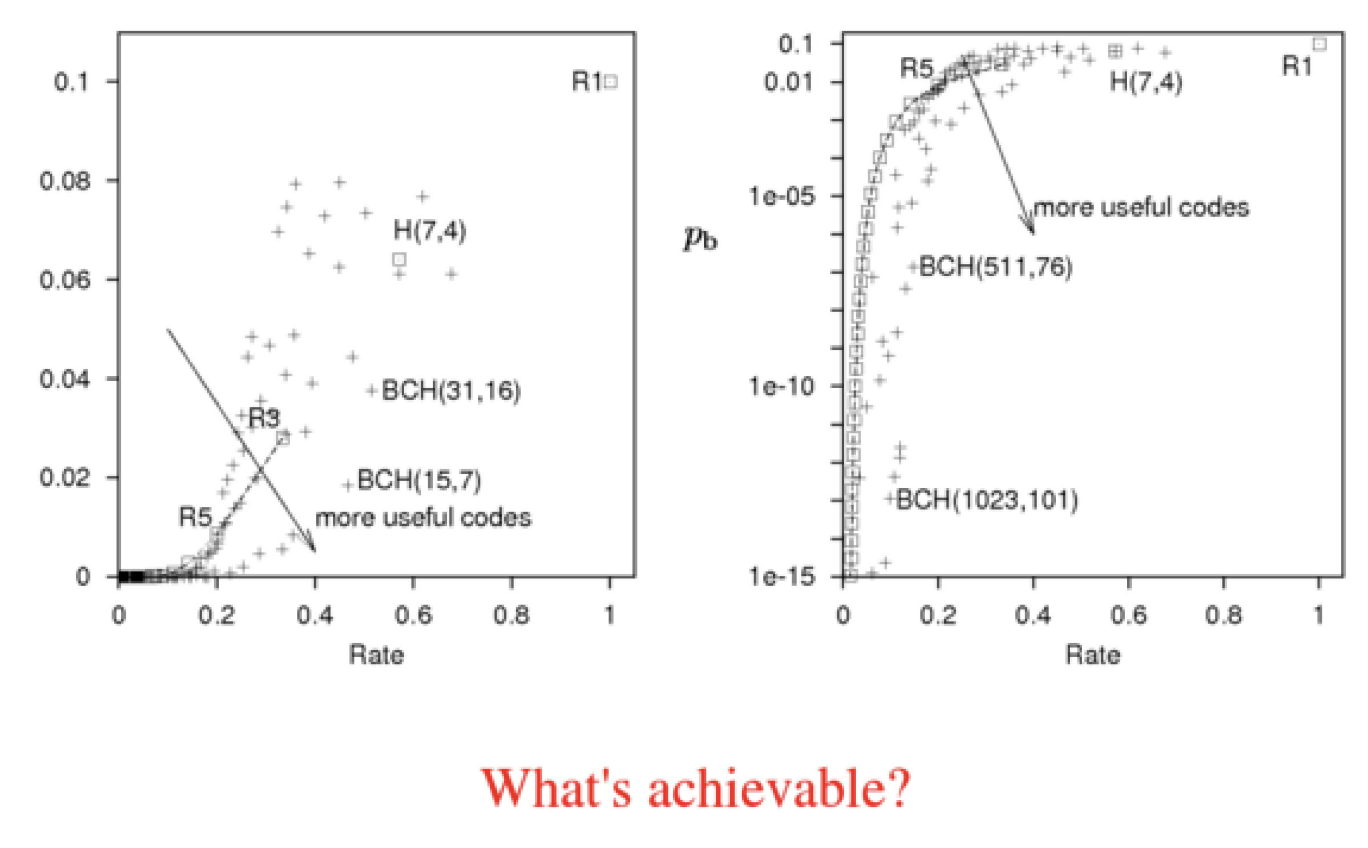
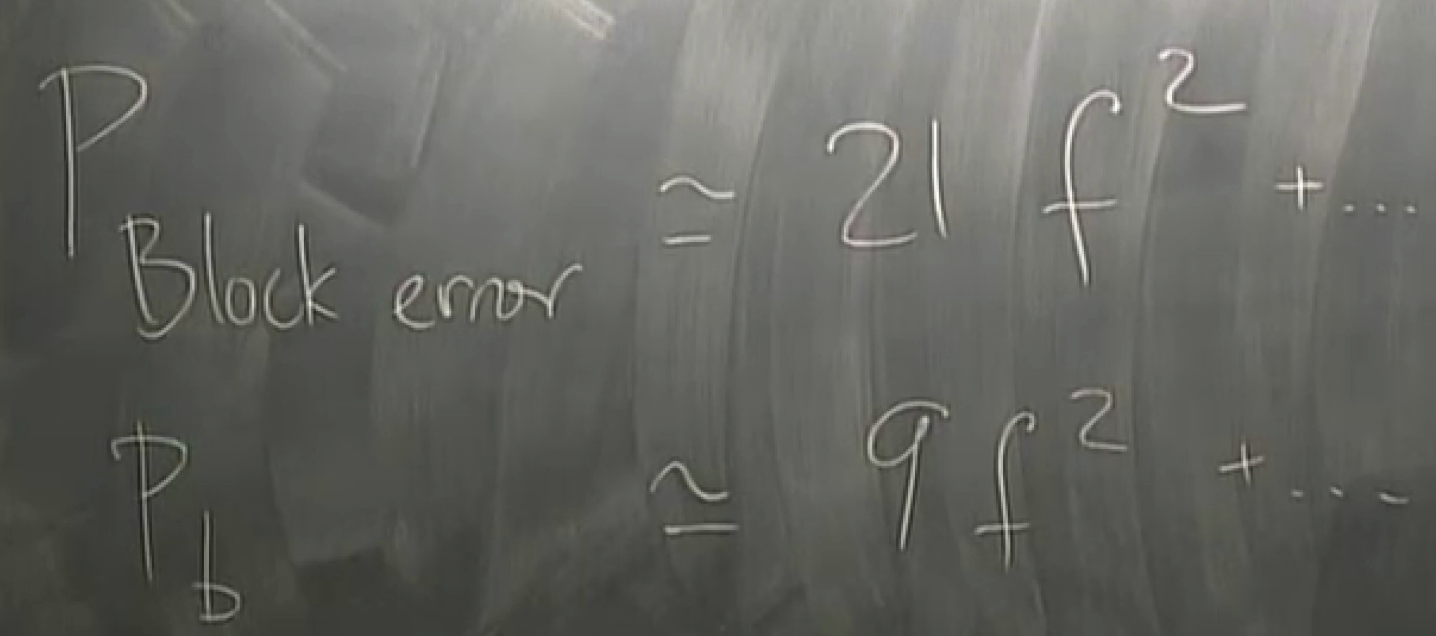
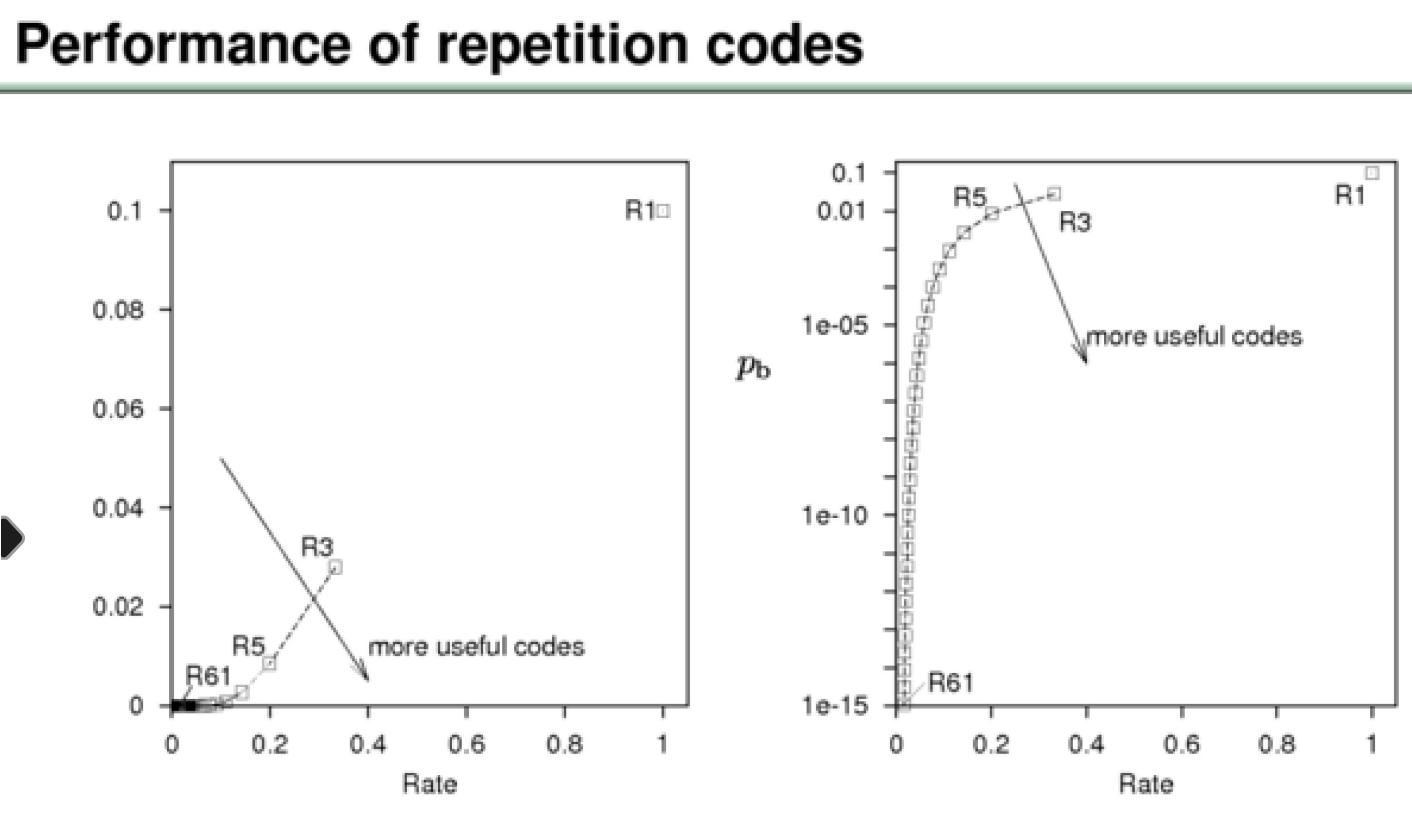
 Shanon proved that you can  get the error probability arbitrarily small , without the rate having to go to zero

and the boundary between achievable and unachievable is the green line

 

 C is the capacity

 

 

 

 

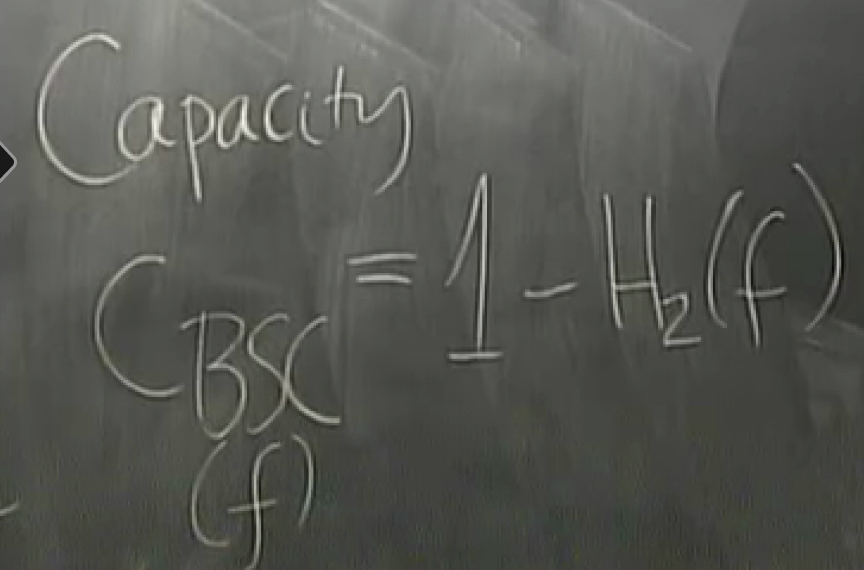
 binary symmetric channel : bsc

 

binary entropy function

 

eg, f=0.1 => H2f = 0.53 => only two disk in the box and there exists an encoding system and a decoding system that can correct as many errors as you want (< all errors).

=> shanon's noisy channel coding theorem