CSP-J/S2019试题选做
S D1T2 括号树
设\(f[u]\)表示根到\(u\)的路径上有多少子串是合法括号串。(即题目里的\(k_u\),此变量名缺乏个性,故换之)
从根向每个节点dfs,容易求出\(c[u]\):表示从根到\(u\)的路径上,我们能匹配则匹配,最后剩下多少个待匹配的左括号。 例如如下\(s_u\)对应的\(c[u]\):
-
((()\(c[u]=2\)。 -
(())(\(c[u]=1\)。 -
(()()\(c[u]=1\)。 -
()))(\(c[u]=1\)。 -
(()())\(c[u]=0\)。
如果\(u\)节点上括号为)且\(c[u]\geq 0\),说明可以以\(u\)节点为结尾,形成一个新的合法子序列。我们大胆猜想,满足上述两个条件时,\(f[u]=f[fa(u)]+1\),否则\(f[u]=f[fa(u)]\)。 可惜过不了大样例。 仔细分析一下发现我们漏算了很多子串。
如:对于\(s_u=\)(()(),因为\(f[4]=1\),所以我们会认为\(f[5]=2\),但其实\(f[5]\)应该等于\(3\),我们漏算了\([2,5]\)这个合法子串。 事实上,我们这样做只计算出了以\(u\)结尾的最短合法子串。问题就出在,当序列结尾形成一个新的合法子串时,它可能和前面原本已经闭合的的子串拼在一起,结合形成“并列式”子串。 极端的例子如(()()()()中\([8,9]\)这个子串,可以和\([6,7]\)拼,也可以和\([4,7]\)拼,甚至可以和\([2,7]\)拼在一起,分别构成新的并列式子串。
我们称:在同一个括号中的、并列出现的、合法的子串为同一层里的子串。如:(()()( () )) ()中,\([2,3],[4,5],[6,9]\)在同一层,\([1,10],[11,12]\)在同一层。
发现两个合法子串在同一层的条件是:结尾位置的\(c[i]\)相同,且两个子串中间没有经过过一个\(c[x]<c[i]\)的部分。如:(()()) (())里的\([2,3]\)和\([8,9]\)就不在同一层,因为它们是\(c[i]=1\),但中间经过了一个\(c[6]=0<1\)。
如果子串结尾位置为\(i\),我们称\(c[i]=k\)的子串位于第\(k\)层。
那么对每个\(u\),我们要求出,从根到\(u\)的路径上,每一层有多少个并列的合法子串。这样,我们就能知道\(c[u]\)这一层有多少合法子串能和“以\(u\)结尾的最短合法子串”拼接。
看起来这需要一个二维的数组来记录。但我们发现,从“以\(fa(u)\)结尾的串里每一层有多少并列的合法子串”,到“以\(u\)结尾的串里每一层有多少并列的合法子串”,这当中的修改是很小且很特殊的:当\(u\)上是)时,\(c[u]\)这一层会多一个并列的合法子串,而\(c[i]>c[u]\)的这些层,它们的并列合法子串数将清零,这是根据我们前面分析出的“两个合法子串在同一层的条件”中要求它们之间不能存在一个\(c[x]<c[i]\),现在\(u\)就是这个\(x\)了。
先从父亲处继承,然后单点\(+1\),并把这个点的后缀清零。主席树可以实现。
时间、空间复杂度:\(O(n\log n)\)。
参考代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=5e5+5;
struct EDGE{int nxt,to;}edge[MAXN];
int head[MAXN],tot;
inline void add_edge(int u,int v){edge[++tot].nxt=head[u];edge[tot].to=v;head[u]=tot;}
int n,rt[MAXN],ls[MAXN*30],rs[MAXN*30],val[MAXN*30],cnt;
void modify(int &x,int y,int l,int r,int pos){
x=++cnt;val[x]=val[y];ls[x]=ls[y];rs[x]=rs[y];
val[x]++;
if(l==r)return;
int mid=(l+r)>>1;
if(pos<=mid)modify(ls[x],ls[y],l,mid,pos),rs[x]=0;
else modify(rs[x],rs[y],mid+1,r,pos);
}
int query(int x,int l,int r,int pos){
if(!x)return 0;
if(l==r)return val[x];
int mid=(l+r)>>1;
if(pos<=mid)return query(ls[x],l,mid,pos);
else return query(rs[x],mid+1,r,pos);
}
ll f[MAXN],c[MAXN];
char s[MAXN];
void dfs(int u){
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
f[v]=f[u];c[v]=c[u];rt[v]=rt[u];
if(s[v]=='('){
if(c[v]<0)c[v]=0,rt[v]=0;
c[v]++;
}
else {
c[v]--;
if(c[v]>=0){
f[v]++;
f[v]+=query(rt[v],0,n,c[v]);
modify(rt[v],rt[v],0,n,c[v]);
}
}
dfs(v);
}
}
int main(){
// freopen("brackets.in","r",stdin);
// freopen("brackets.out","w",stdout);
scanf("%d%s",&n,s+1);
for(int i=2,fa;i<=n;++i)scanf("%d",&fa),add_edge(fa,i);
if(s[1]=='(')c[1]=1;else c[1]=-1;
dfs(1);
ll ans=0;
for(int i=1;i<=n;++i)ans^=((ll)i*f[i]);
//cout<<f[i]<<" ";cout<<endl;
//
cout<<ans<<endl;
return 0;
}
S D1T3 树上的数
我看了wqy大佬的题解并决定盗用他的图(雾
首先考虑一条链的情况。
我们观察链上某个节点\(u\)上的数字变动情况。可以发现无论我们先删左边还是先删右边,原来它上面的数字一定会被搬运到了其中一个方向,同时另一个方向一定又过来了一个数,此外还有一个数字反向经过了\(u\)。
也就是下面这种情况(这里是先删除右边那条边):
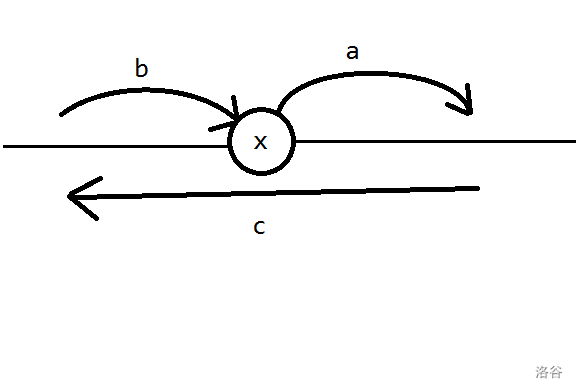
再考虑菊花,即围绕着节点\(u\)有多条出边的情况。如果把这些边排成一圈依次拆掉,我们先会把\(u\)上的数挪到某个与它相邻的节点上。然后从这个节点开始,按顺时针顺序,这一圈上每个数依次从\(u\)的某条边进入,然后从顺时针的下一条边出去。最后某个数会进入\(u\)然后不再出去,这就是最终留在\(u\)上的数了。
如果画出来会很优美:
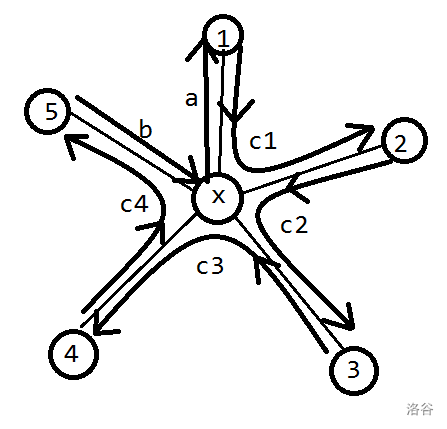
因为是求字典序最小,显然应该按数字\(1\)到\(n\)贪心,每个数字都挪到它能挪到的编号最小的节点上。
不妨以当前数字所在的节点为根。我们做一遍dfs,判断每个点是否能被挪到。节点\(u\)能被挪到,其实分为两个部分的条件:
-
根到\(u\)的路径上(不包括根和\(u\))每个节点都能够作为“中转节点”(图中一进一出的那种);
-
\(u\)自己能够作为终点节点(图中只进不出的那种)。
考虑条件1,对于每个\(v\),我们要判断的其实是能否从根一路通畅地走入\(v\)的子树。我们称满足这样条件的\(v\)为“合法”。
-
如果\(v\)的父亲\(fa(v)\)不合法,则\(v\)肯定也不合法。
-
如果\(fa(v)\)到\(v\)的这条边已经被以相同的方向使用过,则\(v\)不合法。(根据上图,显然每条边最终都会被以两个方向各走一遍,此处我们只要判断\(fa(v)\)走向\(v\)的方向是否被走过)
-
如果\(fa(v)\)不为根,我们从\(fa(fa(v))\)走到\(fa(v)\),再走向\(v\),相当于在\(fa(v)\)这个节点上一进一出。我们加入这一进一出的路径后,如果恰好把\(fa(v)\)周围所有经过它的路径串成了一圈(首尾相接),但是\(fa(v)\)周围仍然存在还没走过的边,则我们现在还不能走这一进一出。即\(v\)不合法。【注:这部分比较复杂,请结合图和代码仔细理解,具体的实现方式下面会讲。】
考虑条件2,我们判断一个点\(u\)能否作为终点,方法和判\(v\)类似。
-
如果\(u\)已经存在一条只进不出的边了,则\(u\)不能作为终点。(根据图来看显然每个点只能有一次只进不出的机会。根据实际含义来说就是,之前已经有别的数以\(u\)作为终点了,所以\(u\)不能作为当前数的终点)
-
如果\(fa(u)\)到\(u\)的这条边已经被以相同的方向使用过,则\(u\)不能作为终点。
-
如果加入\(fa(u)\)到\(u\)的路径后,\(u\)周围的路径会被串成一圈,但\(u\)周围仍然存在还没走过的边,则\(u\)现在还不能作为终点。
这样,对于每个数我们贪心地选编号最小的、能作为终点的点即可。选出后我们暴力更新这个点到根路径上的信息。
下面讲一些具体实现的问题:
判断一条边以哪个方向走过是比较容易的。需要注意的是:我们的根在不断变化,所以不能以“是从父亲走向儿子”还是“从儿子走向父亲”来判断。我是直接建了个二维的邻接表,state[u][v]=u表示\(u,v\)间的边从\(u\)到\(v\)走过,state[u][v]=v表示\(u,v\)间的边从\(v\)到\(u\)走过,state[u][v]=0表示两个方向都走过,state[u][v]=-1表示两个方向都没走过。
如何判断加入一条路径后,\(u\)周围的所有路径是否会被串成一圈?由于路径是有方向的,若干路径会串成一条链,我们记一条链的开头为\(st\),结尾为\(ed\)。新加入的路径如果是一进一出,那么我们要判断,如果:进入的那头的链的\(st\)是\(u\)上数字移出的边,走出的那头的链的\(ed\)是\(u\)上数字移入的边,加入这一进一出后,就会把所有边串成一条链了。
所谓\(u\)上数字移入、移出的边是指:对于每个节点\(u\),都会有唯一的一条移出的边,也会有唯一的一条移入的边。如上图中\(x\rightarrow 1\)就是移出,\(5\rightarrow x\)就是移入。【这部分请结合图和代码重点理解】
最开始时,\(u\)周围的每条边都是一条单独的链。当我们加入一进一出的路径,我们实际上是连起了两条链。这个“连起”的过程,我们可以用并查集维护:对每个\(u\)都开一个并查集,维护它周围的每条链的\(st\)和\(ed\)。一进一出时,进的那条链提供合并后的\(st\),出的那条链提供合并后的\(ed\)。
最后,请注意特判\(n=1\)时的情况,因为我们的程序中默认每个点都会移出去一次、移进来一次,而\(n=1\)时这种情况根本不会发生。
时间复杂度\(O(n^2\alpha)\),空间复杂度\(O(n^2)\)。
参考代码:
//problem:P5659
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef pair<int,ll> pil;
typedef pair<ll,int> pli;
namespace Fread{
const int MAXN=1<<20;
char buffer[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buffer)+fread(buffer,1,MAXN,stdin);
if(S==T)return EOF;
}
return *S++;
}
}
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
inline int read(){
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int MAXN=2005;
struct EDGE{int nxt,to;}edge[MAXN<<1];
int head[MAXN],tot;
inline void add_edge(int u,int v){edge[++tot].nxt=head[u],edge[tot].to=v,head[u]=tot;}
int n,p[MAXN],d_nu[MAXN],d_in[MAXN],d_out[MAXN],frm[MAXN],to[MAXN],state[MAXN][MAXN];
struct DSU{
int fa[MAXN],st[MAXN],ed[MAXN],sz[MAXN];
int get_fa(int x){
return x==fa[x]?x:(fa[x]=get_fa(fa[x]));
}
void union_s(int frm,int to){
int x=get_fa(frm),y=get_fa(to);
if(x==y)return;
if(sz[x]<sz[y])fa[x]=y,st[y]=st[x],sz[y]+=sz[x];
else fa[y]=x,ed[x]=ed[y],sz[x]+=sz[y];
}
int get_st(int x){
return st[get_fa(x)];
}
int get_ed(int x){
return ed[get_fa(x)];
}
void Init(int x){
fa[x]=st[x]=ed[x]=x;sz[x]=1;
}
}b[MAXN];
/*
tips:
p[num] -> node
d_nu[u]: edge(from u) not used
stata[u][v]:
- -1 not used
- u u->v
- v v->u
- 0 u->v & v->u
*/
int Root,fa[MAXN];
bool flag[MAXN];
void dfs(int u){
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa[u])continue;
fa[v]=u;
flag[v]=1;
//能否经过u,到达v
if(!flag[u])flag[v]=0;
else if(u!=Root){
if(state[u][fa[u]]==0||state[u][fa[u]]==fa[u]||state[u][v]==0||state[u][v]==u)flag[v]=0;
else if(flag[v]&&b[u].get_st(fa[u])==to[u]&&b[u].get_ed(v)==frm[u]&&d_in[u]+d_out[u]+d_nu[u]*2-2!=0)flag[v]=0;
else if(flag[v]&&b[u].get_ed(v)==fa[u])flag[v]=0;
}
else{
//assert(!to[u]);
if(state[u][v]==0||state[u][v]==u)flag[v]=0;
else if(flag[v]&&b[u].get_ed(v)==frm[u]&&d_in[u]+d_out[u]+d_nu[u]*2-1!=0)flag[v]=0;
}
dfs(v);
}
//能否以u为终点
if(u==Root)flag[u]=0;
else{
if(frm[u])flag[u]=0;
else if(flag[u]&&b[u].get_st(fa[u])==to[u]&&d_in[u]+d_out[u]+d_nu[u]*2-1!=0)flag[u]=0;
}
}
void Init(){
tot=0;
for(int i=1;i<=n;++i){
head[i]=0;
d_nu[i]=d_in[i]=d_out[i]=frm[i]=to[i]=0;
}
}
int main() {
int Testcases=read();while(Testcases--){
Init();
n=read();
for(int i=1;i<=n;++i)p[i]=read();
if(n==1){
puts("1");
continue;
}
for(int i=1,u,v;i<n;++i){
u=read(),v=read(),add_edge(u,v),add_edge(v,u);
d_nu[u]++,d_nu[v]++;
b[u].Init(v),b[v].Init(u);
state[u][v]=state[v][u]=-1;
}
for(int i=1;i<=n;++i){
Root=p[i];
fa[Root]=0,flag[Root]=1;
dfs(Root);
int res=0;
for(int j=1;j<=n;++j)if(flag[j]){res=j;break;}
//assert(res!=0&&res!=Root);
printf("%d ",res);
int u=res;
frm[u]=fa[u];
while(fa[u]!=Root){
//assert(state[u][fa[u]]==state[fa[u]][u]);
if(state[u][fa[u]]==-1){
state[u][fa[u]]=state[fa[u]][u]=fa[u];
d_nu[u]--,d_nu[fa[u]]--;
d_in[u]++,d_out[fa[u]]++;
}else{
//assert(state[u][fa[u]]==u);
state[u][fa[u]]=state[fa[u]][u]=0;
d_in[fa[u]]--,d_out[u]--;
}
int v=u;
u=fa[u];
b[u].union_s(fa[u],v);
}
to[Root]=u;
if(state[u][fa[u]]==-1){
state[u][fa[u]]=state[fa[u]][u]=fa[u];
d_nu[u]--,d_nu[fa[u]]--;
d_in[u]++,d_out[fa[u]]++;
}else{
//assert(state[u][fa[u]]==u);
state[u][fa[u]]=state[fa[u]][u]=0;
d_in[fa[u]]--,d_out[u]--;
}
}
puts("");
}
return 0;
}
S D2T1 Emiya 家今天的饭
总结一下要求:
-
总共要选至少一个位置(不能不选)。
-
每行至多选一个位置。
-
每列选的位置数量不超过所选总数的\(\frac{1}{2}\)。
部分分:\(m=2\)或\(3\)时,以\(m=3\)为例,我们可以设\(dp[i][a][b][c]\)表示考虑了\(i\)行,第\(1\)列选了\(a\)个,第\(2\)列选了\(b\)个,第\(3\)列选了\(c\)个的方案数。统计答案时要求\(a,b,c\leq\lfloor\frac{a+b+c}{2}\rfloor\)即可。复杂度\(O(n^{m+1})\)。我考场上就写的这个,得到了64分的好成绩。
发现每列不超过\(\frac{1}{2}\)这个限制很特殊。如果我们枚举哪些列不合法,那么容易发现,不合法的列至多只有\(1\)列。所以我们枚举那一个不合法的列,然后求出:在强制这一列不合法的前提下的方案数。
设\(dp[i][j][k]\)表示考虑了前\(i\)行,共选了\(j\)个数,强制不合法的列选了\(k\)个数,时的方案数。复杂度\(O(n^3m)\),可以得到\(84\)分的高分(Orz pmt!)。
考虑优化,其实我们关系的只是\(j\)和\(k\)之间的关系。具体地,最后我们要求\(k>\lfloor\frac{j}{2}\rfloor\),即\(2k-j>0\)。所以我们可以把\([j][k]\)两维压成一维:令\(dp[i][x]\)表示考虑了前\(i\)行,\(2k-j=x\)时的方案数即可。由于\(x\)可能\(<0\),所以在具体实现时我们把第二维的值统一加\(n\)。
时间复杂度\(O(n^2m)\)。
参考代码:
//problem:P5664
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
inline int read(){
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int MOD=998244353;
inline int mod(int x){return x<MOD?(x<0?x+MOD:x):x-MOD;}
int n,m,a[105][2005],s[105],dp[105][205];
int main() {
n=read();m=read();int ans=1;
for(int i=1;i<=n;++i){for(int j=1;j<=m;++j)a[i][j]=read(),s[i]=mod(s[i]+a[i][j]);ans=(ll)ans*(s[i]+1)%MOD;}
ans=mod(ans-1);
for(int l=1;l<=m;++l){
memset(dp,0,sizeof(dp));
dp[0][n]=1;
for(int i=0;i<n;++i){
for(int j=n-i;j<=n+i;++j){
if(!dp[i][j])continue;
dp[i+1][j+1]=mod(dp[i+1][j+1]+(ll)dp[i][j]*a[i+1][l]%MOD);
dp[i+1][j-1]=mod(dp[i+1][j-1]+(ll)dp[i][j]*mod(s[i+1]-a[i+1][l])%MOD);
dp[i+1][j]=mod(dp[i+1][j]+dp[i][j]);
}
}
for(int j=n+1;j<=n+n;++j)ans=mod(ans-dp[n][j]);
}
cout<<ans<<endl;
return 0;
}
S D2T2 划分
部分分:设\(dp[i][j]\)表示考虑了前\(i\)个数,当前段的结束位置为\(i\),上一段的结束位置为\(j\)时的最小代价。转移时枚举上上段的结束位置\(k\),从\(dp[j][k]\)转移。对于每个\(i,j\),合法的\(k\)一定是一段后缀(位置可以二分出来),所以记录\(dp\)第二维的后缀最小值即可转移,复杂度\(O(n^2\log n)\)。
我们为什么要用dp的第二维记录一个\(j\)呢?我们把一个东西记录在dp的一维里,必然是因为这个东西“有得有失”。比如做背包时,加入一个物品,增加了价值,但同时也增加了重量。我们不知道如何去平衡这个得失,或者说不知道在此时最优的情况所带来的的“失”是否会使全局更劣,于是我们单开一维,把每一种情况都记录下来,从而保证不错过全局最优解。
回到本题,我们之所以不设\(dp[i]\),是因为这样我们不知道上一段的和是什么,缺少条件,不好转移。但是如果用一个数组记录下每一个\(i\)是从哪里转移过来的呢?这样我们能否保证,对\(j\)最有利的转移点,也同时最有利于\(j\)后面所有需要从\(j\)转移的点?也就是说,如果这个问题的答案是肯定的,那么不存在“有的有失”的情况,当前最优即全局最优,我们直接贪心、直接钦定,不用经过第二维DP的权衡。
考虑每次转移时,选择满足条件的(上一段的和\(\leq\)当前段和的)点中最靠后的转移。
可以证明,这样做一定是最优的。
备注:我在网上找到了两篇证明,但是证明并不优美且没啥扩展价值,所以就不展开了。附两个链接供读者参考。
感性理解一下结论好像又很显然(雾)
在此结论的基础上,每个位置\(i\)的上一段的结束位置就是确定的了,我们记为\(pre(i)\)。对\(a\)做前缀和,我们记\(s_i=\sum_{j=1}^{i}a_j\)。
则最优的转移点\(pre(i)\)一定是所有满足\(s_i-s_j\geq s_j-s_{pre(j)}\)的\(j\)中最大的。把这个条件转化一下就是\(2s_j-s_{pre(j)}\leq s_i\)。
我们维护一个单调队列。在这个队列中,从队首到队尾,元素的下标单调递增,队内元素\(j\)的\(2s_j-s_{pre(j)}\)也单调递增。因为如果存在一个\(k<j\)使得\(2s_k-s_{pre(k)}\geq2s_j-s_{pre(j)}\),则\(k\)在任何时候都不会有用。
当需要从\(i\)转移时,我们检查队首。如果队首的下一个元素满足转移条件,则可以把队首弹掉。因为我们总是取满足条件的元素中下标最大的。而\(s_i\)是单调递增的,这个队首如果现在没有用,以后就再也不会有用了。
复杂度\(O(n)\)。
为了避免空间爆炸,我们只开一个长度为\(n\)的数组,即前缀和数组。其他的信息都用结构体或pair装在单调队列里,这样使用的内存大小为任意时刻的最大队列长度,显然是\(\leq n\)的。
参考代码:
//problem:P5665
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef pair<int,ll> pil;
typedef pair<ll,int> pli;
namespace Fread{
const int MAXN=1<<20;
char buffer[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buffer)+fread(buffer,1,MAXN,stdin);
if(S==T) return EOF;
}
return *S++;
}
}
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
inline int read(){
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int MAXN=4e7+5;
int n;
ll s[MAXN];
__int128 dp[MAXN];
void big_input(){
int x,y,z,b[2],pj,lj,rj;
x=read(),y=read(),z=read(),b[1]=read(),b[0]=read(),read();
const int moood=(1<<30);
pj=0;
for(int i=1,j=0;i<=n;++i){
if(i>pj){
++j;
pj=read();lj=read();rj=read();
}
if(i>2)b[i&1]=((ll)b[(i&1)^1]*x+(ll)b[i&1]*y+z)%moood;
s[i]=s[i-1]+(b[i&1]%(rj-lj+1))+lj;
}
}
void print(__int128 ans){
const ll base=1e18;
if(ans<base)cout<<(ull)ans<<endl;
else{
cout<<(ll)(ans/base);
ll t=ans%base;int len=0;
while(t)len++,t/=10;
for(int i=1;i<=18-len;++i)cout<<"0";
if(ans%base)cout<<(ll)(ans%base)<<endl;
}
}
int main() {
n=read();int ty=read();
if(!ty)for(int i=1;i<=n;++i)s[i]=s[i-1]+read();
else big_input();
dp[0]=0;
deque<pli>dq;dq.push_back(mk(0,0));
for(int i=1;i<=n;++i){
while(dq.size()>1&&s[i]>=dq[1].fst)dq.pop_front();
__int128 d=s[i]-s[dq.front().scd];dp[i]=dp[dq.front().scd]+d*d;
while(!dq.empty()&&dq.back().fst>=s[i]+d)dq.pop_back();
dq.push_back(mk(s[i]+d,i));
}
print(dp[n]);
return 0;
}
S D2T3 树的重心
不妨先令\(1\)为根。考虑以根作为重心的贡献。
设根最大的子树大小为\(mx\)。
-
如果割掉的边不在最大的子树内,则割去的子树大小\(t\)要满足\(mx\times 2\leq n-t\),即\(t\leq n-mx\times 2\);
-
否则,割掉的边在最大的子树内,设次大子树大小为\(smx\),则割去子树大小\(t\)要满足:\(smx\times 2\leq n-t,(mx-t)\times 2\leq n-t\),即\(mx\times2-n\leq t\leq n-smx\times2\)。
我们用线段树合并求出每个节点子树内每种大小的子树分别有多少。枚举根的每个儿子,分别在根的线段树上做区间查询,就得到了根作为重心的出现次数。
如果暴力枚举根,每次重新做线段树合并,则复杂度\(O(n^2\log n)\)。
考虑换根。发现如果以\(u\)为根,则相比于以\(fa(u)\)为根,在线段树上的变化:只会增加一个\(n-size_u\),减少一个\(size_u\)。在dfs时用一个树状数组维护根到当前节点的路径上,哪些\(size\)值被增加了,哪些\(size\)值被减少了,回溯时在树状数组上消除贡献即可。
需要注意的是,线段树合并后,原线段树上的信息就会被覆盖,所以我们不能在换根时再到\(u\)的线段树上进行查询,而要在第一遍dfs到\(u\)时就把换根需要的查询信息预处理好。
参考代码:
//problem:P5666
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef pair<int,ll> pil;
typedef pair<ll,int> pli;
namespace Fread{
const int MAXN=1<<20;
char buffer[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buffer)+fread(buffer,1,MAXN,stdin);
if(S==T)return EOF;
}
return *S++;
}
}
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
inline int read(){
int t;cin>>t;return t;
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int MAXN=3e5;
struct EDGE{int nxt,to;}edge[MAXN<<1];
int n,head[MAXN],tot;
inline void add_edge(int u,int v){edge[++tot].nxt=head[u],edge[tot].to=v,head[u]=tot;}
int rt[MAXN];
struct SegmentTree{
int cnt,ls[MAXN*40],rs[MAXN*40],sum[MAXN*40];
void modify(int &p,int l,int r,int pos,int x){
if(!p)p=++cnt;assert(cnt<MAXN*40);
sum[p]+=x;
if(l==r)return;
int mid=(l+r)>>1;
if(pos<=mid)modify(ls[p],l,mid,pos,x);
else modify(rs[p],mid+1,r,pos,x);
}
int merge(int x,int y){
if(!x||!y)return x+y;
int z=++cnt;assert(cnt<MAXN*40);
sum[z]=sum[x]+sum[y];
ls[z]=merge(ls[x],ls[y]);
rs[z]=merge(rs[x],rs[y]);
return z;
}
int query(int p,int l,int r,int ql,int qr){
if(ql>qr||!p)return 0;
if(ql<=l&&qr>=r)return sum[p];
int mid=(l+r)>>1,res=0;
if(ql<=mid)res=query(ls[p],l,mid,ql,qr);
if(qr>mid)res+=query(rs[p],mid+1,r,ql,qr);
return res;
}
void Init(){
for(int i=1;i<=cnt;++i)ls[i]=rs[i]=sum[i]=0;cnt=0;
}
SegmentTree(){}
}T1;
int sz[MAXN],f[MAXN],L[MAXN],R[MAXN];
void dfs1(int u,int fa){
sz[u]=1;
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa)continue;
dfs1(v,u);
sz[u]+=sz[v];
}
int mx=n-sz[u],smx=0;
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa)continue;
if(sz[v]>mx)smx=mx,mx=sz[v];
else if(sz[v]>smx)smx=sz[v];
}
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa)continue;
if(smx==mx||sz[v]!=mx){
f[u]+=T1.query(rt[v],1,n,1,n-2*mx);
}else{
f[u]+=T1.query(rt[v],1,n,2*mx-n,n-2*smx);
}
}
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa)continue;
rt[u]=T1.merge(rt[u],rt[v]);
}
if(fa){
if(smx==mx||n-sz[u]!=mx){
f[u]-=T1.query(rt[u],1,n,L[u]=1,R[u]=n-2*mx);
}else{
f[u]-=T1.query(rt[u],1,n,L[u]=2*mx-n,R[u]=n-2*smx);
}
T1.modify(rt[u],1,n,sz[u],1);
}
}
ll ans;
struct BIT{
int c[MAXN];
void modify(int p,int x){
for(;p<=n;p+=(p&(-p)))c[p]+=x;
}
int query(int p){
int res=0;
for(;p;p-=(p&(-p)))res+=c[p];
return res;
}
int query(int l,int r){
l=max(l,1),r=min(r,n);
if(l>r)return 0;
return query(r)-query(l-1);
}
void Init(){
memset(c,0,sizeof(int)*(n+3));
}
BIT(){}
}T2;
void dfs2(int u,int fa){
if(fa){
T2.modify(sz[u],-1);
T2.modify(n-sz[u],1);
f[u]+=T1.query(rt[1],1,n,L[u],R[u])+T2.query(L[u],R[u]);
}
//cout<<"* "<<u<<" "<<f[u]<<endl;
ans+=(ll)u*f[u];
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==fa)continue;
dfs2(v,u);
}
if(fa){
T2.modify(sz[u],1);
T2.modify(n-sz[u],-1);
}
}
void Init(){
memset(head,0,sizeof(int)*(n+3));tot=0;
memset(rt,0,sizeof(int)*(n+3));T1.Init();
T2.Init();
memset(f,0,sizeof(int)*(n+3));
}
int main() {
//freopen("data.txt","r",stdin);
int Testcases=read();while(Testcases--){
Init();
n=read();
for(int i=1,u,v;i<n;++i)u=read(),v=read(),add_edge(u,v),add_edge(v,u);
//for(int i=1;i<=n;++i)ans+=(ll)i*solve_root(i);
dfs1(1,0);
ans=0;dfs2(1,0);
printf("%lld\n",ans);
}
return 0;
}
J T2 公交换乘
设\(P=\max_{i=1}^{n}\{price_i\}\)。我敲了一个O(nP)的模拟就直接AC了(大雾)
\(O(nP)\)代码片段:
const int MAXN=1e5+5;
int n;
struct node{int type,price,t;}a[MAXN];
deque<int>dq[1005];
int main() {
n=read();
for(int i=1;i<=n;++i)a[i].type=read(),a[i].price=read(),a[i].t=read();
int ans=0;
for(int i=1;i<=n;++i){
if(a[i].type==0){
ans+=a[i].price;
dq[a[i].price].push_back(i);
}
else{
int opt=-1;
for(int j=a[i].price;j<=1000;++j){
while(!dq[j].empty()&&a[dq[j].front()].t<a[i].t-45)dq[j].pop_front();
if(!dq[j].empty()){
if(opt==-1||a[dq[j].front()].t<a[dq[opt].front()].t)opt=j;
}
}
if(opt==-1)ans+=a[i].price;
else dq[opt].pop_front();
}
}
cout<<ans<<endl;
return 0;
}
这里讲一下\(O(n\log P)\)的做法。
我们开一棵下标为票价的值域的线段树。线段树的每个叶子节点上放一个deque。非叶子节点存子树内每个deque的front(首元素)的最小值(deque里存的值是车票的编号,其最小值也就是出现时间最早的车票)。特别地,如果一个deque为空,则令该叶子的值为无穷大。
对于一辆地铁,我们直接在它对应的票价的deque上新加入(push_back)一个下标。
对于一辆公交,我们要查询所有尚未使用的、票价不超过\(price_i\)的车票里时间最早的。相当于在线段树上查询一段后缀的最小值。
-
如果最小值\(<t_i-45\),则直接将其弹出,因为它已经过期,以后也不会再有用了。继续查询。
-
如果查询到的最小值为无穷大,说明所有合法的票价都为空了,我们没有匹配到合法的地铁,这辆公交车必须自己买票。
-
否则说明查到了一班合法的地铁。将其弹出(表示已使用)。
因为每辆地铁只会入队列、出队列一次,每次加入、弹出时涉及到的线段树操作是\(O(\log P)\)的。所以总复杂度\(O(n\log P)\)。
参考代码:
//problem:P5661
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
namespace Fread{
const int MAXN=1<<20;
char buffer[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buffer)+fread(buffer,1,MAXN,stdin);
if(S==T)return EOF;
}
return *S++;
}
}
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
inline int read(){
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int MAXN=1e5+5,MAXP=1005,INF=1e9;
int n;
struct node{int type,price,t;}a[MAXN];
struct SegmentTree{
int val[MAXP],pos[MAXN<<2];
deque<int>dq[MAXP];
void push_up(int p){
pos[p]=(val[pos[p<<1]]<=val[pos[p<<1|1]]?pos[p<<1]:pos[p<<1|1]);
}
void build(int p,int l,int r){
if(l==r){
val[l]=INF;
pos[p]=l;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
push_up(p);
}
void modify(int p,int l,int r,int pos,int x){
if(l==r){
if(x==-1){
assert(!dq[l].empty());
dq[l].pop_front();
val[l]=(dq[l].empty()?INF:dq[l].front());
}
else{
dq[l].push_back(x);
val[l]=dq[l].front();
}
return;
}
int mid=(l+r)>>1;
if(pos<=mid)modify(p<<1,l,mid,pos,x);
else modify(p<<1|1,mid+1,r,pos,x);
push_up(p);
}
int query(int p,int l,int r,int ql,int qr){
if(ql<=l&&qr>=r)return pos[p];
int mid=(l+r)>>1,res=0;
if(ql<=mid)res=query(p<<1,l,mid,ql,qr);
if(qr>mid){
int x=query(p<<1|1,mid+1,r,ql,qr);
if(!res||val[res]>val[x])res=x;
}
assert(res!=0);
return res;
}
}T;
int main() {
n=read();
for(int i=1;i<=n;++i)a[i].type=read(),a[i].price=read(),a[i].t=read();
T.build(1,1,1000);
int ans=0;
for(int i=1;i<=n;++i){
if(a[i].type==0){
ans+=a[i].price;
T.modify(1,1,1000,a[i].price,i);
}
else{
while(true){
int x=T.query(1,1,1000,a[i].price,1000);
if(T.val[x]==INF){
ans+=a[i].price;
break;
}
else if(a[T.val[x]].t<a[i].t-45){
T.modify(1,1,1000,x,-1);
}
else{
T.modify(1,1,1000,x,-1);
break;
}
}
}
}
cout<<ans<<endl;
return 0;
}
J T3 纪念品
由于同一天内是可以既卖出又买入的,如果我们要将一样纪念品连续持有好几天,则我们可以视作在中间的每一天既卖出、又买入,这样我们可以在每天刚开始的时候,把手上所有的纪念品都换成钱,如果要继续持有,就在今天晚上再换回来。这样的好处是我们只需要DP出当天把所有纪念品换成钱后手上最多有多少钱即可,不用考虑其它资产。
设\(f(i)\)表示第\(i\)天,把所有纪念品换成钱后,手上最多有多少钱。用这些钱我们可以在当天买纪念品、在下一天卖掉,从而在下一天得到更多的钱。
在每一天内,我们可能会买很多种不同的纪念品。设\(g(x)\)表示在当前天,用\(x\)元钱,最多能在第二天(通过把手上的纪念品卖掉)换得多少钱。这相当于是完全背包的模型,因为每样纪念品可以在钱数足够的情况下买无限多个。每样纪念品都是背包的物品,它们的重量是它们在当前天的价格,而它们的价值是它们在下一天的价格。
对第\(i\)天,求出\(g\)后,则\(f(i+1)=g(f(i))\)。
边界是\(f(1)=m\)。
复杂度\(O(TVn)\),其中\(V\)是任意时刻的最大金币数量。
参考代码:
//problem:P5662
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
namespace Fread{
const int MAXN=1<<20;
char buffer[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buffer)+fread(buffer,1,MAXN,stdin);
if(S==T)return EOF;
}
return *S++;
}
}
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
inline int read(){
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int t,n,m,a[105][105],f[105],g[10004];
int main() {
t=read(),n=read(),m=read();
for(int i=1;i<=t;++i)for(int j=1;j<=n;++j)a[i][j]=read();
f[1]=m;
for(int i=1;i<t;++i){
g[0]=0;
for(int j=1;j<=10000;++j){
g[j]=max(j,g[j-1]);
for(int k=1;k<=n;++k)if(j>=a[i][k])g[j]=max(g[j],g[j-a[i][k]]+a[i+1][k]);
}
f[i+1]=g[f[i]];
}
cout<<f[t]<<endl;
return 0;
}
J T4 加工零件
发现编号为\(a\)的工人生产第\(L\)阶段的零件,需要\(1\)提供原材料,当且仅当存在一条\(1\)到\(a\)的路径长度为\(L\)。因为这个“路径”是允许在同一条边上来回横跳的,每横跳一次路径长度加\(2\),所以我们可以把条件改为:当且仅当存在一条\(1\)到\(a\)的路径,长度\(\leq L\)且奇偶性和\(L\)相同。
所以我们从\(1\)出发,对每个点求从\(1\)到它的奇数最短路和偶数最短路即可。因为每个点只会被入队、出队各一次,所以复杂度\(O(n)\)。
参考代码:
//problem:P5663
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fst first
#define scd second
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
namespace Fread{
const int MAXN=1<<20;
char buffer[MAXN],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buffer)+fread(buffer,1,MAXN,stdin);
if(S==T)return EOF;
}
return *S++;
}
}
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#endif
inline int read(){
int f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll readll(){
ll f=1,x=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int MAXN=1e5+5,INF=0x3f3f3f3f;
struct EDGE{int nxt,to;}edge[MAXN<<1];
int n,m,q,head[MAXN],tot;
inline void add_edge(int u,int v){edge[++tot].nxt=head[u],edge[tot].to=v,head[u]=tot;}
int dis[MAXN][2];
void dij(){
memset(dis,0x3f,sizeof(dis));
dis[1][0]=0;
queue<pii>q;q.push(mk(1,0));
while(!q.empty()){
int u=q.front().fst,t=q.front().scd;q.pop();
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
int nd=t+1;
if(nd<dis[v][nd&1]){
dis[v][nd&1]=nd;
q.push(mk(v,nd));
}
}
}
}
int main() {
n=read();m=read();q=read();
for(int i=1,u,v;i<=m;++i)u=read(),v=read(),add_edge(u,v),add_edge(v,u);
dij();
while(q--){
int u=read(),t=read();
if(dis[u][t&1]<=t)puts("Yes");
else puts("No");
}
return 0;
}

