线性支持向量机中的硬间隔(hard margin)和软间隔(soft margin)
intro
The support-vector mechine is a new learning machine for two-group classification problems. The machine conceptually implements the following idea: input vectors are non-linearly mapped to a very high-dimension feature space. In this feature space a linear decision surface is constructed. Special properties of the decision surface ensures high generalization ability of the learning machine. The idea behind the support-vector network was previously implemented for the restricted case where the training data can be separated without errors. We here extend this result to non-separable training data.
High generalization ability of support-vector networks utilizing polynomial input transformations is demonstrated. We also compare the performance of the support-vector network to various classical learning algorithms that all took part in a benchmark study of Optical Character Recognition.
摘自eptember 1995, Volume 20, Issue 3, pp 273–297
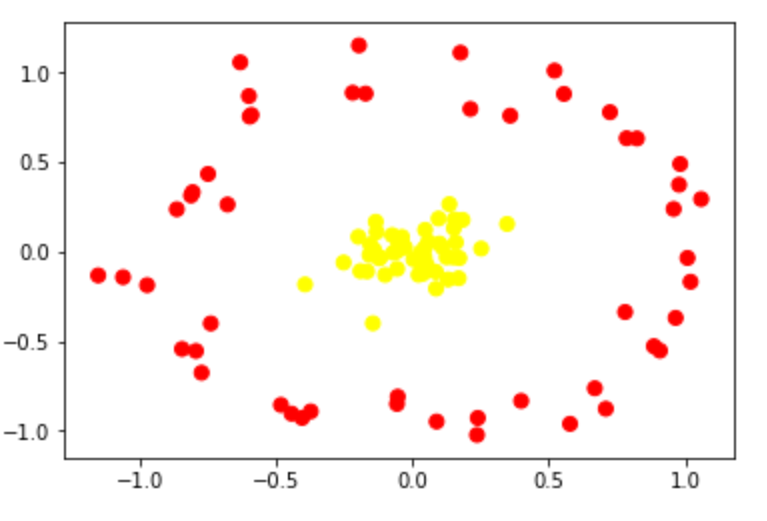
支持向量机: 上世纪流行的一种用来解决二分类问题的算法。我们使用一组样本{ (\(x_{i}\),\(y_{i}\)) }(其中y∈{-1,1},称为标签;\(x_{i}\)为一维向量,称为特征)来构建模型(训练模型)。咋说呢,借助坐标系把这些点的特征在空间中表示出来,使用两种颜色来表示y。需要寻找一个平面把这些点划分为两类。这个平面就是我们的分类器。表示出来一看呢,有的是线性可分的,有的是线性不可分的。分别如下面二图:
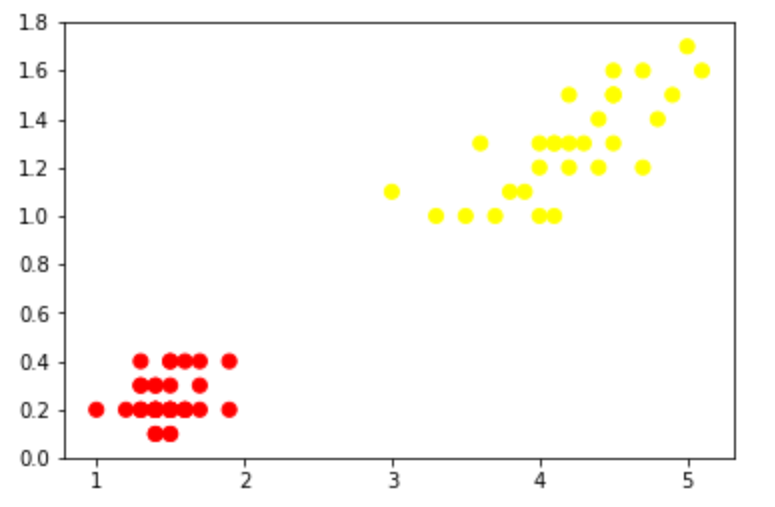
SVM刚诞生时遇到的问题大多都如前者,这样我们直接计算“最大间隔超平面”就ok,这个称为“线性支持向量机”,即最初的SVM;(作者————1963年,万普尼克)
后来,遇到了更多复杂的情况(如第二张图),大家希望能改进SVM,使它也能够很好地处理后者,于是把核技巧拿到了SVM上,借助核函数\(\phi(x_{i})\)将原特征向量映射到高维空间,使它可以一刀划分开来(像上面的左图),再计算“最大间隔超平面”。经过这一改进之后,SVM的泛化能力大大加强。这个称为“非线性支持向量机”。(作者————1992年,Bernhard E. Boser、Isabelle M. Guyon和弗拉基米尔·万普尼克)
explanation
1962年提出的线性支持向量机中有两个概念:“硬间隔”,“软间隔”。
如果我们的训练数据集是线性可分的,那么可以找到一个超平面将训练数据集严格地划开,分为两类(可以想象成一个平板)。我们找两个这样的超平面,它们满足1.两者平行2.两者距离最大(即下图中的两条虚线)。两个超平面上的样本x们称为”支持向量“。“最大间隔超平面”(也就是分类器)是两超平面的平均值。我们定义这两个超平面间的区域为“间隔”。在这种情况下它就是“硬间隔”。
最大间隔超平面可以表示为: W*X+b = 0
两个超平面可以分别表示为: WX+b = 1,WX+b = -1

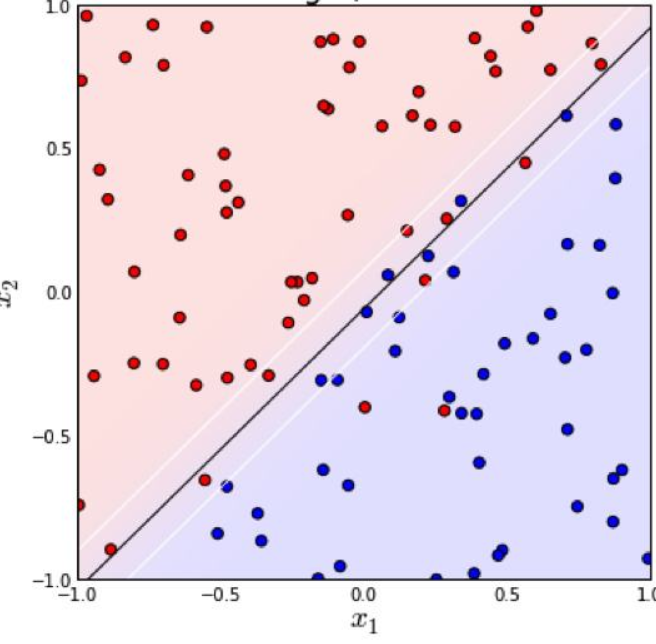
对于数据线性不可分的情况(上图),我们引入铰链损失函数:\({\displaystyle \max \left(0,1-y_{i}({\vec {w}}\cdot {\vec {x_{i}}}-b)\right)}\)。
当约束条件 (1) 满足时(也就是如果 \(x_{i}\) 位于边距的正确一侧)此函数为零。对于间隔的错误一侧的数据,该函数的值与距间隔的距离成正比。 然后我们希望最小化(参数\(\lambda\) 用来权衡增加间隔大小与确保 \(x_{i}\) 位于间隔的正确一侧之间的关系)
\({\displaystyle \left[{\frac {1}{n}}\sum _{i=1}^{n}\max \left(0,1-y_{i}({\vec {w}}\cdot {\vec {x_{i}}}-b)\right)\right]+\lambda \lVert {\vec {w}}\rVert ^{2},}\)
这时的“间隔”就是“软间隔”。
总结一下,我们构建模型使用的数据集如果是严格可一刀分开的, 那么两超平面间的间隔就是“硬间隔”;如果不是严格可以一刀分开的,两超平面间的间隔就是“软间隔”。这是针对线性支持向量机而言。哈哈哈有人说了线性支持向量机都五十年前的东西了,还不如说说非线性支持向量机。进入非线性支持向量机时代后,“硬间隔”“软间隔”是对于核函数变换后的超平面而言的了。
现在对付“软间隔”我们都用“泛化”和“拟合”了,上世纪机器学习刚起步的时候可没这么多东西。可以说是冷兵器时代,如今科技发达,处理二分类问题我们可以用很多技术——逻辑回归啊,神经网络啊,各种聚类算法啊,等等。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号