02(c)多元无约束优化问题-牛顿法
此部分内容接《02(a)多元无约束优化问题》!
第二类:牛顿法(Newton method)
\[f({{\mathbf{x}}_{k}}+\mathbf{\delta })\text{ }\approx \text{ }f({{\mathbf{x}}_{k}})+{{\nabla }^{T}}f({{\mathbf{x}}_{k}})\cdot \mathbf{\delta }+\frac{1}{2}{{\mathbf{\delta }}^{T}}\cdot {{\nabla }^{2}}f({{\mathbf{x}}_{k}})\cdot \mathbf{\delta }\]
在${{\mathbf{x}}_{k}}$定了的情况下,$f({{\mathbf{x}}_{k}}+\mathbf{\delta })\text{ }$可以看成是$\mathbf{\delta }$的函数,要使函数达到极小值点,即找出使得函数$f({{\mathbf{x}}_{k}}+\mathbf{\delta })$对$\mathbf{\delta }$的一阶导数等于0,则有:
\[\begin{aligned}& f({{\mathbf{x}}_{k}}+\mathbf{\delta }{)}'\text{ }=\nabla f({{\mathbf{x}}_{k}})+{{\nabla }^{2}}f({{\mathbf{x}}_{k}})\cdot \mathbf{\delta } \\& \text{ =}\nabla f({{\mathbf{x}}_{k}})+H({{\mathbf{x}}_{k}})\cdot \mathbf{\delta }=0 \\\end{aligned}\]
则下降方向可写为:$\mathbf{\delta }=-{{H}^{-1}}({{\mathbf{x}}_{k}})\cdot \nabla f({{\mathbf{x}}_{k}})$。
(听课的时候就一直在想,一阶导数等于零的点就是极小值点吗???$y=a{{x}^{2}}+bx+c$一种简单的一元二次函数的一阶导数等于0的点,是不是极小值点,还的看$a$的正负呢!)
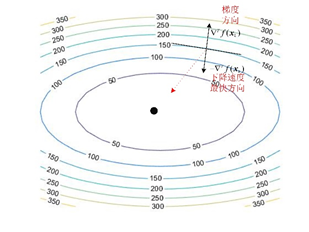
图 1
从上图中可以看出,在点${{\mathbf{x}}_{k}}$处使函数下降最快的方向是$-\nabla f({{\mathbf{x}}_{k}})$方向,但它却不是使$f({{\mathbf{x}}_{k}})$最快接近最小值的方向(最快接近最小值方向应该是上图中红色虚线的方向);由此见牛顿法的下降方向:$\mathbf{\delta }=-{{H}^{-1}}({{\mathbf{x}}_{k}})\cdot \nabla f({{\mathbf{x}}_{k}})$,就是在$-\nabla f({{\mathbf{x}}_{k}})$乘上了一个该点Hessian阵的逆${{H}^{-1}}({{\mathbf{x}}_{k}})$;我们希望的是在乘上${{H}^{-1}}({{\mathbf{x}}_{k}})$后使得下降方向朝向上图中红色虚线的方向;But,在有些情况下乘上${{H}^{-1}}({{\mathbf{x}}_{k}})$后,不但没有使函数值$f({{\mathbf{x}}_{k}})$下降,反而让函数值$f({{\mathbf{x}}_{k}})$变大了。只有当${{H}^{-1}}({{\mathbf{x}}_{k}})$在满足下面的条件下,才能使函数值不断减小:
\[\begin{aligned}& {{\left( -\nabla f({{\mathbf{x}}_{k}}) \right)}^{T}}\cdot \left( -{{H}^{-1}}({{\mathbf{x}}_{k}})\cdot \nabla f({{\mathbf{x}}_{k}}) \right)=\left\| -\nabla f({{\mathbf{x}}_{k}}) \right\|\cdot \left\| -{{H}^{-1}}({{\mathbf{x}}_{k}})\cdot \nabla f({{\mathbf{x}}_{k}}) \right\|\cos(\theta ) \\& \text{ =}{{\nabla }^{T}}f({{\mathbf{x}}_{k}})\cdot {{H}^{-1}}({{\mathbf{x}}_{k}})\cdot \nabla f({{\mathbf{x}}_{k}})>0 \\\end{aligned}\]
即要使从新获得的下降方向$-{{H}^{-1}}({{\mathbf{x}}_{k}})\cdot \nabla f({{\mathbf{x}}_{k}})$与最速下降方向$-\nabla f({{\mathbf{x}}_{k}})$之间的夹角$-{\pi }/{2}\;<\theta <{\pi }/{2}\;$。要满足:
\[{{\nabla }^{T}}f({{\mathbf{x}}_{k}})\cdot {{H}^{-1}}({{\mathbf{x}}_{k}})\nabla f({{\mathbf{x}}_{k}})>0\]
${{H}^{-1}}({{\mathbf{x}}_{k}})$要达到什么样的条件呢,由正定二次型的性质可知,当${{H}^{-1}}({{\mathbf{x}}_{k}})$为正定阵(等价于${{H}^{-1}}({{\mathbf{x}}_{k}})\succ 0$的全部特征值大于0)时,式(12)恒成立;当${{H}^{-1}}({{\mathbf{x}}_{k}})$不是正定阵的情况下仍然希望使用牛顿法,则需要对最速下降方向$-\nabla f({{\mathbf{x}}_{k}})$前面乘的Hessian阵的逆${{H}^{-1}}({{\mathbf{x}}_{k}})$进行改进;由于${{H}^{-1}}({{\mathbf{x}}_{k}})$为一个实对称阵,所以一定能正交分解,这里取${{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{n}}$从大到小排:
\[{{H}^{-1}}({{\mathbf{x}}_{k}})=U\left[ \begin{matrix}{{\lambda }_{1}} & {} & {} & {} \\{} & {{\lambda }_{2}} & {} & {} \\{} & {} & \ddots & {} \\{} & {} & {} & {{\lambda }_{n}} \\\end{matrix} \right]{{U}^{T}}\]
具体步骤:
s1:找出${{H}^{-1}}({{\mathbf{x}}_{k}})$的最小特征值:Matlab代码可写为$\min (eig({{H}^{-1}}({{\mathbf{x}}_{k}})))=-9.8$;
s2:组合得到一个新的${{\hat{H}}^{-1}}({{\mathbf{x}}_{k}})={{H}^{-1}}({{\mathbf{x}}_{k}})+9.9E$;
\[\begin{aligned}& {{{\hat{H}}}^{-1}}({{\mathbf{x}}_{k}})=U\left[ \begin{matrix}{{\lambda }_{1}} & {} & {} & {} \\{} & {{\lambda }_{2}} & {} & {} \\{} & {} & \ddots & {} \\{} & {} & {} & -9.8 \\\end{matrix} \right]{{U}^{T}}+9.9UE{{U}^{T}} \\& \text{ }=U\left[ \begin{matrix}{{\lambda }_{1}}+9.9 & {} & {} & {} \\{} & {{\lambda }_{2}}+9.9 & {} & {} \\{} & {} & \ddots & {} \\{} & {} & {} & 0.1 \\\end{matrix} \right]{{U}^{T}}\succ 0 \\\end{aligned}\]
这里由于$U$为正交阵,故由$U{{U}^{T}}=E$,这样牛顿法的下降方向可写为:
\[\mathbf{\delta }=-{{\hat{H}}^{-1}}({{\mathbf{x}}_{k}})\cdot \nabla f({{\mathbf{x}}_{k}})\]
Step3:通过Step2确定下降方向${{\mathbf{d}}_{k}}$之后,$f({{\mathbf{x}}_{k}}+{{\alpha }_{k}}{{\mathbf{d}}_{k}})$可以看成${{\alpha }_{k}}$的一维函数,这一步的主要方法有(Dichotomous search, Fibonacci search, Goldensection search, quadratic interpolation method, and cubic interpolation method);所确定一个步长${{\alpha }_{k}}>0$,${{\mathbf{x}}_{k+1}}={{\mathbf{x}}_{k}}+{{\alpha }_{k}}{{\mathbf{d}}_{k}}$;
Step4: if走一步的距离$\left\| {{\alpha }_{k}}{{\mathbf{d}}_{k}} \right\|<\varepsilon $,则停止并且输出解${{\mathbf{x}}_{k+1}}$;else $k:=k+1$并返回Step2,继续迭代。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号