【数学建模】灰色系统理论II-Verhulst建模-GM(1,N)-GM(2,1)建模
灰色系统理论中,GM(1,1)建模很常用,但他是有一定适应范围的。
GM(1,1)适合于指数规律较强的序列,只能描述单调变化过程。对于具有一定随机波动性的序列,我们考虑使用Verhulst预测模型,或者GM(2,1)模型。
Verhulst和GM(2,1)适合于非单调的摆动发展序列或者具有饱和状态的 S 形序列。
Verhulst预测模型
Verhulst模型的定义如下:
对于模型参数,使用最小二乘估计有以下结果:
最终,可以求得灰色Verhulst的解为:
Verhulst模型应用:道路交通事故预测
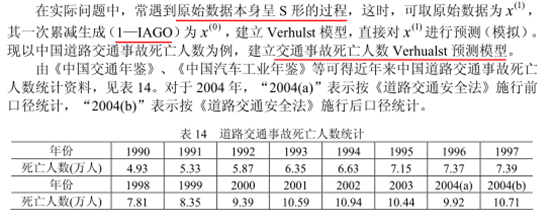
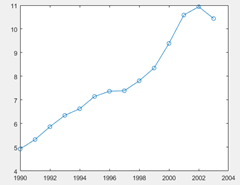
对于交通事故死亡人数统计数据,我们首先做出大体曲线变化图,以从整体上着手。
可见曲线呈现S型,考虑使用verhulst建模。建模过程如下:
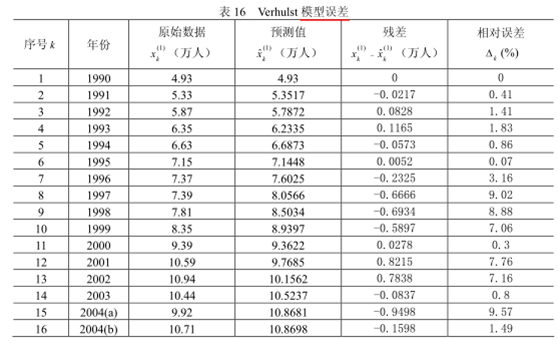
最后我们还要进行一步模型精度检验。灰色模型有一套具体的检验标准,后注。
检验三个指标:相对误差、绝对关联度、均方差比值。利用MATLAB检验结果如下:
可见:
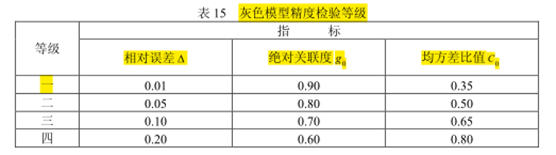
平均相对误差为 3.74% ,则模型精度为二级;同时算得绝对关联度 g 为 0.9845,
均方差比值 C 为 0.2355,则模型精度为一级,可见模型精度较高,可用于事故预测。
附MATLAB程序:
1 clc,clear 2 x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37... 3 7.39 7.81 8.35 9.39 10.59 10.94 10.44]; 4 n = length(x1); 5 nian=1990:2003; 6 plot(nian,x1,'o-'); 7 x0=diff(x1); %作累减生成 8 x0=[x1(1),x0] 9 z1=0.5*(x1(2:n)+x1(1:n-1)) %求紧邻均值生成序列 10 B=[-z1',z1'.^2] 11 Y=x0(2:end)' 12 ab_hat=B\Y %估计参数 a,b 的值 13 x=dsolve('Dx+a*x=b*x^2','x(0)=x0'); %求解常微分方程 14 x=subs(x,{'a','b','x0'},{ab_hat(1),ab_hat(2),x1(1)}); %代入参数值 15 yuce=subs(x,'t',0:14) %计算预测值 16 %下面显示微分方程的解,为了提高计算精度,把该语句放在计算预测值之后 17 x=vpa(x,6) 18 x1_all=[x1,9.92,10.71]; %加上 2004 年的两个观测值 19 yuce(16)=yuce(15); %2004 年有两个观测值,要对应两个相同的预测值 20 epsilon=x1_all-yuce %计算残差 21 delta=abs(epsilon./x1_all) %计算相对误差 22 delta_mean=mean(delta) %计算平均相对误差 23 x1_all_0=x1_all-x1_all(1); %观测值数据列的始点零化像 24 yuce_0=yuce-yuce(1); %预测值数据列的始点零化像 25 s0=abs(sum(x1_all_0(2:end-1))+0.5*x1_all_0(end)); 26 s1=abs(sum(yuce_0(2:end-1))+0.5*yuce_0(end)); 27 tt=yuce_0-x1_all_0; 28 s1_s0=abs(sum(tt(2:end-1))+0.5*tt(end)); 29 absdegree=(1+s0+s1)/(1+s0+s1+s1_s0) %计算灰色绝对关联度 30 c=std(epsilon,1)/std(x1_all,1) %计算标准差比值
灰色预测模型检验标准:
1. 残差合格模型
2. 关联度合格模型
3. 均方差比合格模型
由上可知,给定一组取值,就确定了检验模型精度的一个等级。常用的精度等级见下表:
GM(2,1)模型和DGM模型
1. GM(2,1)模型
弱化算子
对于初期增长势头过于猛烈的模型,为了提高精度,可以考虑使用弱化算子处理原始数列。
对应的,依旧是最小二乘估计参数,再对微分方程求解,得到:
2. DGM(2,1)模型
证明略。
GM(1,N)模型和GM(0,N)模型
1. GM(1,N)
2. GM(0,N)模型
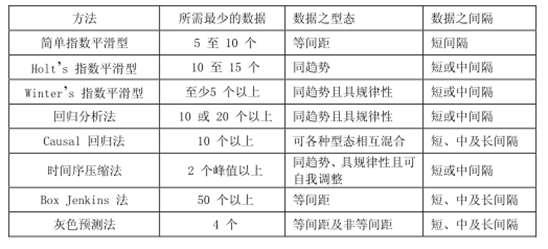
总结:灰色预测法与传统统计方法的比较





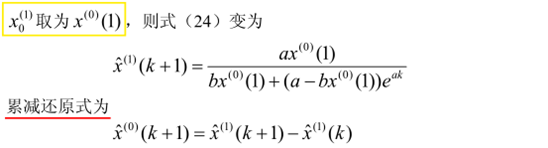














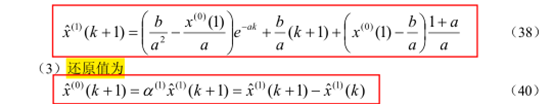


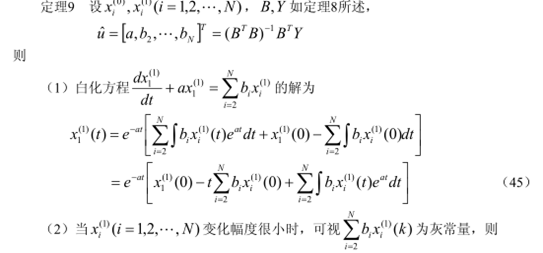



 浙公网安备 33010602011771号
浙公网安备 33010602011771号