【数学建模】偏最小二乘回归分析(PLSR)
PLSR的基本原理与推导,我在这篇博客中有讲过。
0.
偏最小二乘回归集成了多元线性回归、主成分分析和典型相关分析的优点,在建模中是一个更好的选择,并且MATLAB提供了完整的实现,应用时主要的问题是:
- 注意检验,各种检验参数:有关回归的检验以及有关多元分析的检验
- 系数众多,容易混淆
- 要清楚原理才能写好论文
- 注意matlab函数plsregress的众多返回值
- 例如累计贡献度,建模时最好列出表格
1.问题:
自变量组 X = [x1,x2…xn] (n组自变量)
因变量组 Y = [y1,y2,…yp] (p组因变量)
考虑到X、Y内部之间的多重相关性,可以使用PLSR建立Y对X的多元回归模型。这是一种多对多回归的模型。
偏最小二乘回归的实现步骤:
- X、Y标准化。若考虑标准化的不对等特性,考虑实现对应分析。
- 求相关系数矩阵。可以把X、Y统一放到一个增广矩阵中,实现求列向量之间的相关系数矩阵(corrcoef实现无需标准化,直接使用原始数据)
- 求主成分对。(求出自变量与因变量的成分,类似于典型相关分析)这里对数其实是min(n-1,p)。求出<u1,v1>、<u2,v2>… 实际上,u、v是原始变量标准化后的线性组合、即投影。
- 计算贡献率表格。计算前k个主成分u对原始变量X的贡献率、v对Y的贡献率(函数直接返回结果)。
- 根据贡献率表格,选取k个主成分对。一般累计贡献率达到90%合适。
- 求出原始变量X对这k个主成分u的回归方程以及Y对u的(不是v!)回归方程。
- 根据6的结果,可以求出因变量组Y与自变量组X的回归方程,但这其实是标准化了的(常数项一定是0),进一步可以还原为真实原始变量的回归方程,这也是我们所要求得的。
- 模型的解释与检验。
- 首先得进行一个回归检验:判定系数R方的检验(接近于1)。计算每一个回归方程的R方,可以列出表格。
- 之后进行交叉有效性检验:交叉系数Qh方 = 1 – (PRESS(h) / SS(h-1))。这是从主成分分析的角度的检验,即检验提取的k个主成分。(这个检验比较复杂,详细看推导)
2.
MATLAB实现命令:
[XL,YL,XS,YS,BETA,PCTVAR,MSE,stats] = plsregress(X,Y,ncomp)
param:
X: 标准化后的原始X数据,每行一个数据组,每列是一项指标,即一个自变量
Y:标准化后的原始Y数据,每行一个数据组,每列是一项指标,即一个因变量
ncomp:选取的主成分对数
return:
XL:自变量的负荷量矩阵。维度是(自变量数*ncomp)。每行是原始数据X对主成分u的回归表达式的系数
YL:因变量的负荷量矩阵。维度是(自变量数*ncomp)。每行是原始数据Y对主成分u的回归表达式的系数
XS:对应于主成分u的得分矩阵(得分说的是主成分的值)。每列是一个主成分得分向量。
如:每一列是一个主成分ui的值!列数是主成分数。
说明:主成分u1是个列向量.
YS:对应于主成分v的得分矩阵。每列是一个v对原始数据Y的线性组合的系数
BETA:最终的回归表达式系数矩阵。每一列对应的,是一个yi对X的回归表达式系数。
PCTVAR:两行的矩阵。
第一行的每个元素代表着自变量提出主成分,相应主成分u的贡献率。(特征值之比,详细见主成分推导)
第二行的每个元素代表着因变量提出主成分,相应主成分v的贡献率。这个贡献率其实是主成分对原始变量的解释能力大下。
MSE:两行的矩阵。剩余标准差矩阵。第一行的第j个元素对应着自变量与他的前j-1个提出成分之间的剩余标准差。第二行对应因变量。
stats:返回4个值。结构体:stats。
W — A p-by-ncomp matrix of PLS weights so that XS = X0*W.
W = a\XS。 W每行是一个主成分得分向量的系数,如:
T2 — The T2 statistic for each point in XS.
Xresiduals — The predictor residuals, that is, X0-XS*XL'.
Yresiduals — The response residuals, that is, Y0-XS*YL'.
3.案例实现:
求Y对X的偏最小二乘回归方程:原始数据:
(前三列为X变量,后两列为Y变量,共20组样本。以下数据保存为pz.txt与matlab源文件同一文件夹下)
191 36 50 5 162 60 189 37 52 2 110 60 193 38 58 12 101 101 162 35 62 12 105 37 189 35 46 13 155 58 182 36 56 4 101 42 211 38 56 8 101 38 167 34 60 6 125 40 176 31 74 15 200 40 154 33 56 17 251 250 169 34 50 17 120 38 166 33 52 13 210 115 154 34 64 14 215 105 247 46 50 1 50 50 193 36 46 6 70 31 202 37 62 12 210 120 176 37 54 4 60 25 157 32 52 11 230 80 156 33 54 15 225 73 138 33 68 2 110 431 % PLSR 偏最小二乘 2 3 clc,clear 4 ab0 = load('pz.txt'); 5 mu = mean(ab0);%均值 6 sig = std(ab0);% 标准差 7 rr = corrcoef(ab0) %相关系数矩阵 8 ab = zscore(ab0); %数据标准化 9 a = ab(:,[1:3]); %标准化的X 10 b = ab(:,[4:end]); %标准化的Y 11 % pls命令需要标准化变量 12 [XL,YL,XS,YS,BETA,PCTVAR,MSE,stats] = plsregress(a,b) 13 contr = cumsum(PCTVAR,2) %每行累计求和,即计算累计贡献率 14 XL 15 YL 16 XS 17 YS 18 xw = a\XS %自变量提出主成分系数,每列对应一个成分,这个就是stats.W 19 yw = b\YS %因变量提出的主成分系数 20 ncomp = input('输入主成分个数') 21 [XL2,YL2,XS2,YS2,BETA2,PCTVAR2,MSE2,stats2] = plsregress(a,b,ncomp) 22 n = size(a,2);% n是自变量个数 23 m = size(b,2); 24 %求原始数据回归方程常数项 25 beta3(1,:) = mu(n+1:end) - mu(1:n)./sig(1:n)*BETA2([2:end],:).*sig(n+1:end); 26 %求原始数据x1,x2...xn的系数,每一列是一个回归方程 27 beta3([2:n+1],:) = (1./sig(1:n))'*sig(n+1:end).*BETA2([2:end],:) 28 bar(BETA2','k') %画直方图
求解结果(部分)假设采用2个主成分
ncomp =
2
系数:
XL2 =-4.1306 0.0558
-4.1933 1.0239
2.2264 3.4441
YL2 =2.1191 -0.9714
2.5809 -0.8398
0.8869 -0.1877主成分得分(每列一个主成分):
XS2 =-0.1036 -0.2050
-0.1241 -0.0577
-0.1463 0.1807
0.1110 0.2358
-0.0785 -0.3927
-0.0369 0.0249
-0.2263 0.0263
0.1199 0.0730
0.2765 0.2263
0.1874 -0.0577
0.0588 -0.2428
0.1198 -0.2420
0.1913 0.2625
-0.7077 0.2635
-0.1327 -0.3375
-0.1208 0.1803
-0.0633 0.0707
0.1933 -0.2712
0.1690 -0.1291
0.3131 0.3917
YS2 =-1.2834 0.1794
-4.6311 1.3388
-0.2845 -0.6256
-1.2265 0.6851
1.6002 -1.0788
-4.5120 1.5408
-2.9777 -0.0114
-2.7548 1.5473
3.9469 -0.4253
10.4846 -2.6373
1.4139 -0.6681
4.8549 -1.1547
5.2890 -1.0550
-7.6800 -0.1989
-5.1793 1.2090
4.5405 -2.0460
-6.4973 2.0374
4.2728 -0.6046
5.5489 -1.3537
-4.9251 3.3215
标准化数据回归方程系数(可以看到常数项系数是0)
BETA2 =0.0000 0.0000 0.0000
-0.0773 -0.1380 -0.0603
-0.4995 -0.5250 -0.1559
-0.1323 -0.0855 -0.0072
贡献率:
PCTVAR2 =0.6948 0.2265
0.2094 0.0295
剩余标准差:
MSE2 =2.8500 0.8699 0.2242
2.8500 2.2531 2.1689
stats2 =W: [3x2 double]
T2: [20x1 double]
Xresiduals: [20x3 double]
Yresiduals: [20x3 double]
最终的回归方程系数矩阵,每列一个方程:
beta3 =47.0375 612.7674 183.9130
-0.0165 -0.3497 -0.1253
-0.8246 -10.2576 -2.4964
-0.0970 -0.7422 -0.0510
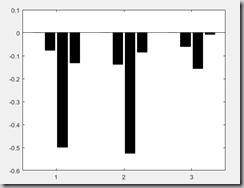
画出回归系数直方图:
还可以用预测的方法做精度分析,在此略过。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号