树的直径

什么是树的直径？

一棵有权值的树上，两点之间的距离为这两点之间的路径权值和，而树的直径就是最远的两个节点的距离，即最大的权值和。

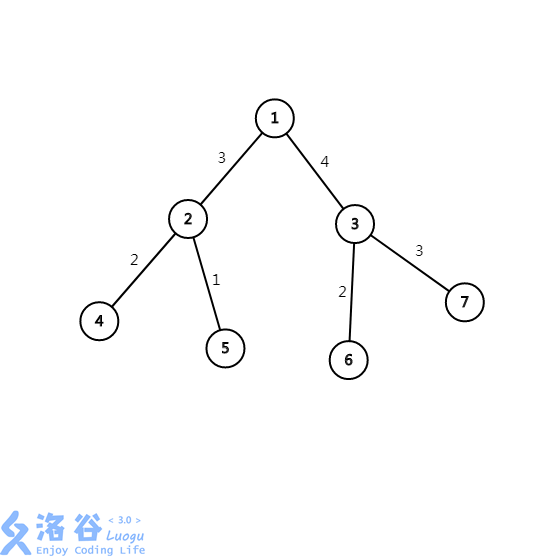
如同上图所示，这棵树的直径就是节点\(4\)与节点\(7\)的距离，长度为\(12\)。

怎么求树的直径？

树的直径通常有两种解法：树形DP，两遍搜索。

树形DP：

树的直径一定是某个节点的子树中不重合的且以这个节点为起点的最长子链和次长子链之和。

如上图，这棵树的直径是\(1\)节点的子树中，\(1-3-7\)（最长链）和\(1-2-4\)（次长链）组成的。

注意，这个点不一定是这棵树的根节点，如下图则是一个反例：

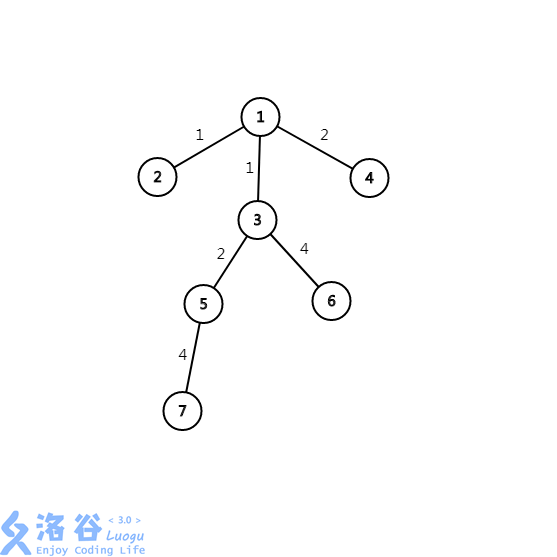
在这张图中，\(3\)号节点子树中的最长链和次长链之和才是这棵树的直径。

我们设\(d[x]\)为从\(x\)出发到达最远叶子节点的距离，若\(x\)是一个父亲节点，\(y_i\)是\(x\)的其中一个子节点，那么\(d[x] = max(d[y_i] + edge[x][y_i])\)。

所以，我们在访问每个节点时，即可求出它的最大链和次大链之和，其中的最大值就是树的直径了。

代码：

void dp (int x) {
	vis[x] = 1;
	for (int i = head[x]; i; i = next[i]) {
		int y = ver[i];
		if (vis[y]) continue;
		dp(y);
		ans = max(ans, d[x] + d[y] + edge[i]);
		//一定有某个时候存在d[x]为最长链而d[y] + edge[i]为次长链或者d[y] + edge[i]为最长链而d[x]为次长链 
		d[x] = max(d[x], d[y] + edge[i]);
	}
}

两遍搜索：

任意取一个节点\(q\)，第一遍搜索寻找距离节点\(q\)最远的节点\(x\)，这个\(x\)必定是这棵树的直径的其中一端。

证明：

如果\(x\)不是直径的其中一端，

若\(q\)在直径上，\(q\)与\(x\)之间的距离加上\(q\)与直径两端其中一端之间的距离显然可以组成一条更长的链，与直径的定义矛盾。
若\(q\)不在直径上，假设\(q\)与直径中最近的节点为\(p\)，那么\(p\)与直径中最远一端的距离小于\(p\)与\(x\)之间的距离（因为\(q\)与直径中最远一端的距离大于\(p\)与直径中最远一端的距离，但是\(q\)与\(x\)之间的距离更长），显然可以组成一条更长的链，与直径的定义矛盾。

之后我们从\(x\)点出发，第二遍搜索寻找距离节点\(x\)最远的节点\(y\)，因为\(x\)是直径的一端，那么\(y\)也必然是直径的另一端。

于是我们就得到树的直径的两端啦！

代码：

void dfs (int x) {
	vis[x] = 1;
	for (int i = head[x]; i; i = nex[i]) {
		int y = ver[i];
		if (vis[y]) continue;
		dis[y] = dis[x] + edge[i];
		dfs(y);
	}
}

试题

T1：模板题

T2：逃学的小孩

T3：巡逻

题解

逃学的小孩：

这道题的大意是：从未知的三点\(A, B, C\)中的\(C\)点出发，先到\(A, B\)最近的点，再到另外一个点的最长距离。

无论\(C\)点在哪，距离它最远的点一定是这棵树的直径的其中一端（上面已经讲过了），我们让这个点为\(A\)点，距离\(A\)最远的另一个点在直径的另外一端，我们设这个点为\(B\)点。

所以显然如果我们要走最长的距离，肯定会经过这棵树的直径的，也就是\(A, B\)之间的距离。

那从\(C\)到\(A\)或者从\(C\)到\(B\)的距离怎么求呢？

现在已知\(A, B\)分别是直径的两端，我们不妨从\(A, B\)出发，计算\(A, B\)分别到其他节点的距离。

之后暴力枚举每个节点\(C_i\)，找到最大的\(min(dis_{C_i, A}, dis_{C_i, B}) +dis_{A, B}\)。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 200010;
int n, m, head[N], ver[N << 1], edge[N << 1], nex[N << 1], tot, vis[N], p, q;
long long dis1[N], dis2[N], dis3[N], ans;
inline void add (int x, int y, int z) {
	ver[++ tot] = y;
	edge[tot] = z;
	nex[tot] = head[x];
	head[x] = tot;
}
void dfs1 (int x) {
	vis[x] = 1;
	for (int i = head[x]; i; i = nex[i]) {
		int y = ver[i];
		if (vis[y]) continue;
		dis1[y] = dis1[x] + edge[i];
		dfs1(y);
	}
}
void dfs2 (int x) {
	vis[x] = 1;
	for (int i = head[x]; i; i = nex[i]) {
		int y = ver[i];
		if (vis[y]) continue;
		dis2[y] = dis2[x] + edge[i];
		dfs2(y);
	}
}
void dfs3 (int x) {
	vis[x] = 1;
	for (int i = head[x]; i; i = nex[i]) {
		int y = ver[i];
		if (vis[y]) continue;
		dis3[y] = dis3[x] + edge[i];
		dfs3(y);
	}
}
int main () {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; i ++) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		add(x, y, z);
		add(y, x, z);
	}
	dfs1(1);
	for (int i = 1; i <= n; i ++)
		if (dis1[p] < dis1[i])
			p = i;
	memset(vis, 0, sizeof(vis));
	dfs2(p);
	for (int i = 1; i <= n; i ++)
		if (dis2[q] < dis2[i])
			q = i;
	memset(vis, 0, sizeof(vis));
	dfs3(q);
	for (int i = 1; i <= n; i ++)
		ans = max(ans, min(dis2[i], dis3[i]) + dis2[q]);
	printf("%lld", ans);
	return 0;
}

巡逻：

根据题意，我们知道\(k\)只有\(1\)或\(2\)两种情况，所以分两种情况讨论。

\(K = 1\)时

由于这是一棵树，所以无论在哪新建一条道路，都会形成一个环。

想一想，如果要以最少的路程巡逻完全部村庄，那这个环是不是只需要走一次就可以了，因为从环上任意一点出发都可以不走重复的路回到原点。

所以应该使这个环尽可能大（因为不在环上的道路必须走两次），很显然只要把直径两端节点间新建一条道路就行啦！

设这个直径大小为\(link1\)，则\(ans = 2 * (n - 1) - link1 + 1\)。

（\(2 * (n - 1)\)是原本要走的长度，由于直径上的道路只需走一次所以减去\(link1\)，最后加上一条新建的道路\(1\)。）

\(K = 2\)时

我们同样可以在直径两端节点新建一条道路连成一个环。

但是还有一条道路可以建，我们需要做的是在图中找出另一个环，使这个环也尽可能大。

这个环也有两种情况，分别是与上一个环有重合或者没有重合。

如果没有重合，那么\(ans = 2 * (n - 1) - link1 + 1 - link2 + 1\)，\(link2\)为最长的且没有与原直径重合的链。

如果有重合，那么\(ans\)变为这两个环互相不重合的部分加上其他道路的长度乘\(2\)，因为重合的部分你需要走两遍（自行脑补一下）！

尝试一下把原直径去掉，重新再图中找出新直径。

这个方法看起来可行，但是由于我们去掉了这个图的一部分，导致这样求出的环只包含第一种情况，也就是不重合的情况，显然答案就不一定最优。

那么不妨把去掉直径换成把直径上的道路边权改为\(-1\)。

改为\(-1\)的原因是把原直径在答案中算上的重复部分加回来，即不把重复部分算进原直径的长度中。

这就巧妙的解决了环重复的问题，所以答案\(ans = 2 * (n - 1) - link1 + 1 - link2 + 1\) 。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 100010;
int n, k, e1[N], e2[N], tot, head[N], ver[N << 1], nex[N << 1], edge[N << 1], fa[N], link1, link2, ring[N], vis[N], dis[N], d[N], ans;
inline void add (int x, int y, int z) {
    ver[++ tot] = y;
    edge[tot] = z;
    nex[tot] = head[x];
    head[x] = tot;
}
void dfs (int x) {
    vis[x] = 1;
    for (int i = head[x]; i; i = nex[i]) {
        int y = ver[i];
        if (vis[y]) continue;
        fa[y] = x;
        dis[y] = dis[x] + edge[i];
        dfs(y);
    }
}
void dp (int x) {
    vis[x] = 1;
    for (int i = head[x]; i; i = nex[i]) {
        int y = ver[i];
        if (vis[y]) continue;
        dp(y);
        link2 = max(link2, d[x] + d[y] + edge[i]);
        d[x] = max(d[x], d[y] + edge[i]);
    }
}
int main () {
    scanf("%d%d", &n, &k);
    ans = (n - 1) * 2;
    for (int i = 1; i < n; i ++) {
        scanf("%d%d", &e1[i], &e2[i]);
        add(e1[i], e2[i], 1);
        add(e2[i], e1[i], 1);
    }
    dfs(1);
    int p = 0;
    for (int i = 1; i <= n; i ++)
    	if (dis[i] > link1) {
    		p = i;
    		link1 = dis[i];
		}
    memset(vis, 0, sizeof(vis));
    link1 = 0;
    fa[p] = 0;
    dis[p] = 0;
    dfs(p);
    int q = 0;
    for (int i = 1; i <= n; i ++)
    	if (dis[i] > link1) {
    		q = i;
    		link1 = dis[i];
		}
    memset(vis, 0, sizeof(vis));
    ans = ans - link1 + 1;
    if (k == 2) {
    	while (q) {
    		ring[q] = 1;
    		q = fa[q];
		}
		memset(head, 0, sizeof(head));
		tot = 0;
		for (int i = 1; i < n; i ++) {
			if (ring[e1[i]] && ring[e2[i]]) {
				add(e1[i], e2[i], -1);
				add(e2[i], e1[i], -1);
			} else {
				add(e1[i], e2[i], 1);
				add(e2[i], e1[i], 1);
			}
		}
		dp(1);
		ans = ans - link2 + 1;
	}
	printf("%d", ans);
    return 0;
}

posted @ 2022-01-12 19:04 duoluoluo 阅读(810) 评论(0) 收藏举报

刷新页面返回顶部