Tarjan算法
Tarjan求强联通分量
什么是强联通分量?
强联通分量即在图中找出一个最大的图,使得这个图上的任意点可以互相到达,一个点也可以算是一个强联通分量。
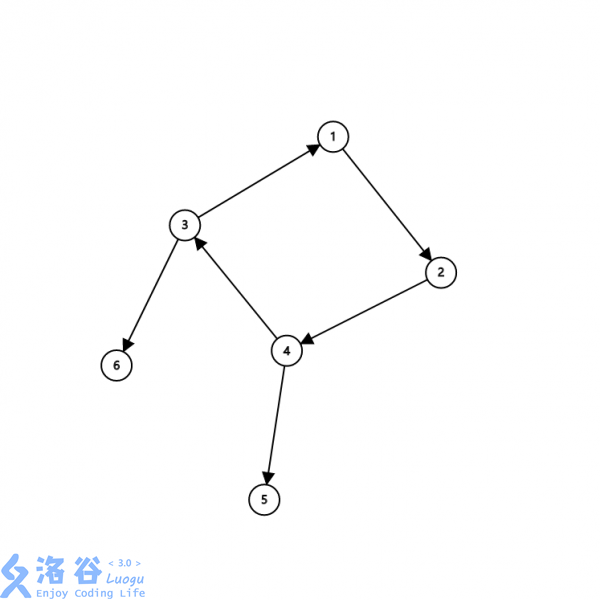
如上图,\(1 - 2 - 4 - 3\)构成了强联通分量,因为它们在一个环上,可以互相到达,同时\(5\)和\(6\)也分别是强联通分量。
怎么求强联通分量?
我们从\(1\)出发开始DFS,可知\(1\)节点在回溯之前会先从\(3\)节点访问到自己,从而得知\(1\)必定与某些节点构成强联通分量。
可是我们要求的是强联通分量,也就是具体哪些点在这个强联通分量中。
是\(1\)下面所有子节点吗?很显然不是,\(5\)和\(6\)都是\(1\)的子节点,但它们并不与\(1\)构成强联通分量。
那到底该怎么办呢?开个栈试试!
我们把已经访问过且还没回溯的节点放进栈中,在DFS的过程中,访问到一个在栈中已经存在的节点(如图中从\(3\)访问\(1\)),那么就开始从栈中一个一个弹出栈顶元素,直到弹到那个被访问的且已经存在的元素(也就是\(1\))。
这个方法确实是正确的,可是代码如何实现呢?
我们需要开四个数组:
\(dfn_i\)表示i节点是第几个被遍历到的节点;
\(low_i\)表示i节点往下遍历能到达的最早访问过的节点,也就是\(dfn_i\)最少的节点(如图中\(low_2 = 1\),\(2\)节点往下遍历能到达\(1\));
\(stack\)表示我们把访问过但是还没回溯的元素放入的栈;
\(vis_i\)表示\(i\)节点是否在栈中。
\(low_i\)也很好求,它的初始值就是\(dfn_i\),假如我们从\(x\)到\(y\)节点,在\(dfs(y)\)回溯之后,\(low_x = min(low_x, low_y)\)。
比如说在图中\(low_1 = 1, low_2 = 2\),在\(dfs(2)\)的过程中,\(2\)会沿着环最后访问到\(1\)节点,这时候\(low_2\)就可以被更新为\(1\)了是吧。
现在回到强联通分量这边,如果我们在\(i\)节点\(dfs\)完回溯后,发现\(dfn_i = low_i\),这时候就可以把栈中元素弹出,直到弹出\(i\)元素,这些被弹出的元素构成了一个强联通分量。
为什么?试想想看,如果一个节点,设为\(x\),它的子节点可以到达比\(x\)更早的祖先,很明显\(low_x\)也会被更新为更早的那个祖先的\(dfn\)。
那所以只有两种情况:
第一种情况:\(x\)的子节点可以到达的祖先也是\(x\)的子节点,如下图,\(1\)的子节点的\(low\)都是\(2\)。
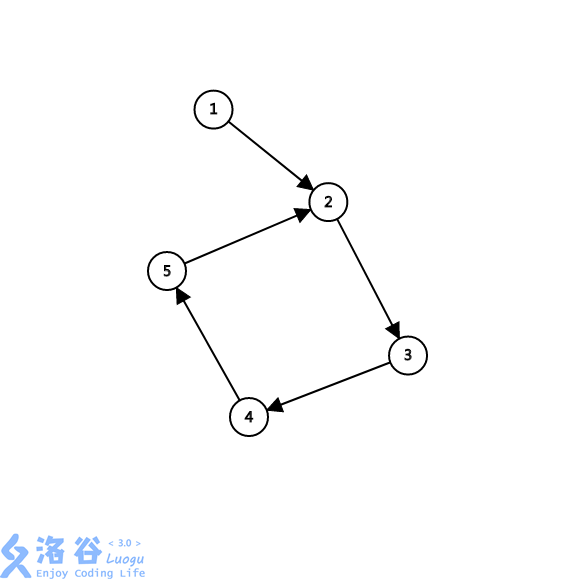
第二种情况:\(x\)的子节点的\(low\)都为\(x\),如下图,\(1\)的子节点的\(low\)都是1。
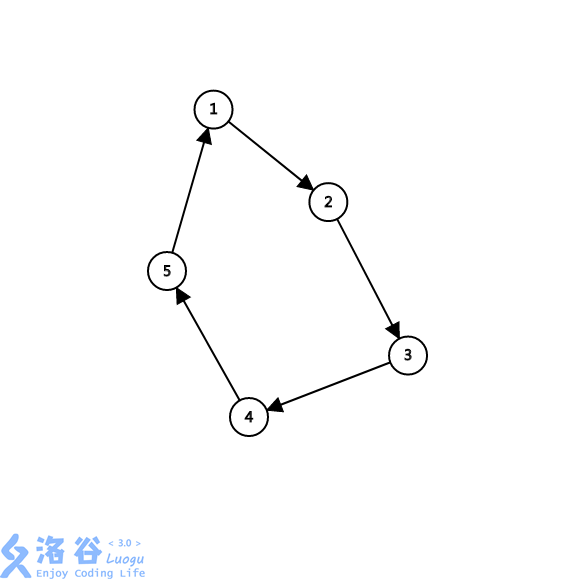
对于第一种情况,我们在\(2\)节点回溯时,就把栈中元素弹出直到弹出\(2\),之后回溯\(1\)的时候,就只剩它自己一个元素了(一个节点也算是一个强联通分量)。
对于第二种情况,不用多说,这一整个都是一个强联通分量吧。
最后给出核心部分代码:
void tarjan (int x) {
dfn[x] = ++ cnt;
low[x] = cnt;
//初始化low[x] = dfn[x] = ++ cnt
sta[++ top] = x;
vis[x] = 1;
//将x元素放入栈
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) {
//因为vis数组标记的是是否在栈中
//所以我们用dfn[y] == 0来判断y节点没有被访问过
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (vis[y]) {
low[x] = min(low[x], low[y]);
//如果y被访问过且不在栈中,说明y已经与其他点构成强联通分量
//虽然x可以访问到y,但是y不能访问到x
//因为如果y可以访问到x,那x也必定与y构成强联通分量
//但事实并不是这样,因此y的祖先并不是x的祖先
//所以只需要当y在栈中时,才需要用low[y]更新low[x]
}
}
//回溯时发现dfn[x] == low[x]
if (dfn[x] == low[x]) {
int sum = 1;
vis[x] = 0;
while (sta[top] != x) {
vis[sta[top --]] = 0;
sum ++; //记录这个强联通分量的节点个数
}
top --;
}
}
来道模板题:牛的舞会
既然是模板题,直接放代码吧:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 10010, M = 50010;
int n, m, head[N], ver[M], Next[M], tot, dfn[N], low[N], vis[N], sta[N], top, cnt, ans;
inline void add (int x, int y) {
ver[++ tot] = y;
Next[tot] = head[x];
head[x] = tot;
}
void tarjan (int x) {
dfn[x] = ++ cnt;
low[x] = cnt;
sta[++ top] = x;
vis[x] = 1;
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
}else if (vis[y])
low[x] = min(low[x], low[y]);
}
if (dfn[x] == low[x]) {
int sum = 1;
vis[x] = 0;
while (sta[top] != x) {
vis[sta[top --]] = 0;
sum ++;
}
top --;
if (sum > 1) ans ++;
}
}
int main () {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i ++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
}
for (int i = 1; i <= n; i ++)
if (!dfn[i])
tarjan(i);
printf("%d", ans);
return 0;
}
Tarjan缩点
什么是缩点?
即把一个强联通分量里的所有点合在一次,这个缩点的点权就是这个强联通分量所有点的点权之和。
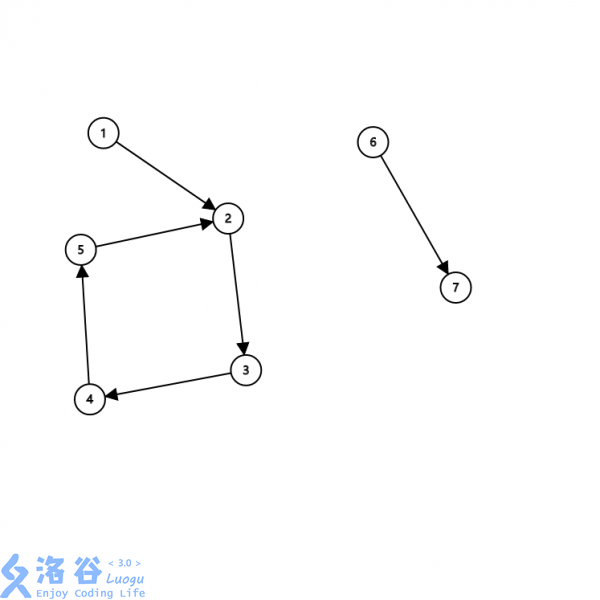
如图中左边的图(\(1 - 2 - 3 - 4 - 5\))缩点后变成右边的图(\(6 - 7\))。
怎么缩点?
代码上还是先Tarjan求强联通分量,把每个强联通分量内的节点都染上颜色(打上不同的标记),如上图\(1\)打上一种标记,\(2 - 3 - 4 - 5\)打上另外一种标记,我们用\(color_x\)表示\(x\)节点所染上的颜色,也可以看成是新图上的点,即缩点。
之后在原图跑一遍dfs,假如当前从\(x\)节点到\(y\)节点,如果\(color_x = color_y\),说明它们的缩点是同一个,在新图上不做任何操作;如果\(color_x ≠ color_y\),说明它们的缩点是不同的,则在新图中连接这两个不同的缩点。
Tarjan缩点对应不同的题有不同的代码,重要的是它是怎么缩点的,下面放出一道缩点的模板题。
题解
很明显这道题需要缩点(题目已经说了),因为为了要获得更大的权值,对于一个强联通分量,把它全部都走一遍显然更优(题目也告诉我们可以重复走),而且由于它是强联通分量,所以全部走一遍不会影响我们的结果。
之后就是缩点啦,怎么缩点上面也讲了,但是缩完点之后我们还要求出新图中权值最大的一条路。
在这里我用了拓扑排序加上DP。
\(f_x\)代表到达\(x\)时可以获得的最大点权和,因为我们刚才已经拓扑排序过了,因此在访问\(x\)时,已经把\(x\)的所有入边都访问过了,这样就可以保证\(f_x\)此时是最优的。
若\(f_x\)此时最优,那么假设\(x\)的出边是\(y\),则\(f_y = max(f_y, f_x + val_y)\),\(val_y\)是\(y\)点的点权。
最后循环每一个点,\(ans = max(f_i)\)。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N = 10010, M = 100010;
int n, m, head1[N], ver1[M], Next1[M], tot1, head2[N], ver2[M], Next2[M], tot2, dfn[N], low[N], vis[N], sta[N], top, cnt, val[N], sum[N], col[N], colCnt, deg[N], tpo[N], tpoCnt, f[N], ans;
inline void add1 (int x, int y) {
ver1[++ tot1] = y;
Next1[tot1] = head1[x];
head1[x] = tot1;
}
inline void add2 (int x, int y) {
ver2[++ tot2] = y;
Next2[tot2] = head2[x];
head2[x] = tot2;
deg[y] ++;
}
void tarjan (int x) {
dfn[x] = ++ cnt;
low[x] = cnt;
sta[++ top] = x;
vis[x] = 1;
for (int i = head1[x]; i; i = Next1[i]) {
int y = ver1[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
}else if (vis[y])
low[x] = min(low[x], low[y]);
}
if (dfn[x] == low[x]) {
sum[++ colCnt] = val[x];
col[x] = colCnt;
vis[x] = 0;
while (sta[top] != x) {
sum[colCnt] += val[sta[top]];
col[sta[top]] = colCnt;
vis[sta[top --]] = 0;
}
top --;
}
}
void newMap (int x) {
vis[x] = 1;
for (int i = head1[x]; i; i = Next1[i]) {
int y = ver1[i];
if (col[x] != col[y])
add2(col[x], col[y]);
if (vis[y])
continue;
newMap(y);
}
}
inline void topo () {
queue <int> q;
for (int i = 1; i <= colCnt; i ++)
if (!deg[i]) {
q.push(i);
tpo[++ tpoCnt] = i;
f[i] = sum[i];
}
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = head2[x]; i; i = Next2[i]) {
int y = ver2[i];
deg[y] --;
if (!deg[y]) {
q.push(y);
tpo[++ tpoCnt] = y;
}
}
}
}
int main () {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++)
scanf("%d", &val[i]);
for (int i = 1; i <= m; i ++) {
int x, y;
scanf("%d%d", &x, &y);
add1(x, y);
}
for (int i = 1; i <= n; i ++)
if (!dfn[i])
tarjan(i);
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= n; i ++)
if (!vis[i])
newMap(i);
topo();
for (int i = 1; i <= tpoCnt; i ++) {
int x = tpo[i];
for (int j = head2[x]; j; j = Next2[j]) {
int y = ver2[j];
f[y] = max(f[y], f[x] + sum[y]);
}
}
for (int i = 1; i <= tpoCnt; i ++)
ans = max(ans, f[i]);
printf("%d", ans);
return 0;
}
Tarjan求割点
什么是割点?
在一张互相连通的图中,如果去掉某个点,会使得剩下的点不能互相连通,那么这个点就是割点。
如下图中,\(2\)为割点。
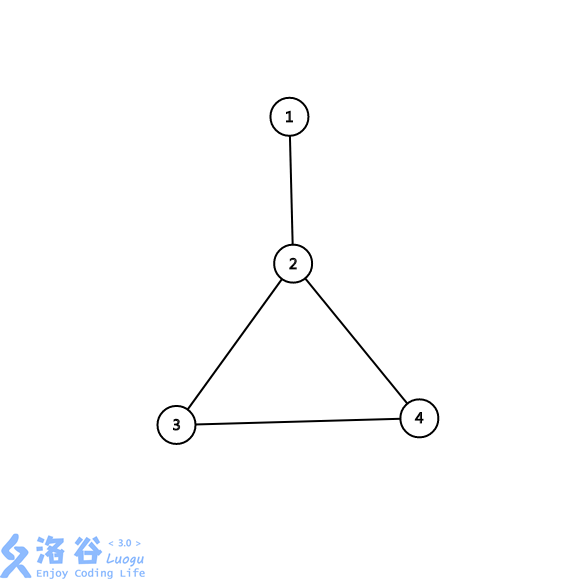
怎么求割点?
一个点是割点有两种情况。
-
根节点有两个或两个以上的不构成环的子节点
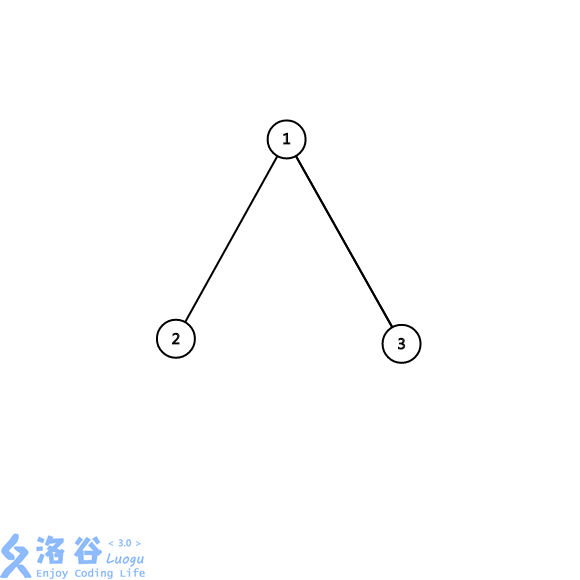
-
不是根节点也不是叶子节点且与某个不跟自己构成环的点相连
下面这张图中\(2, 5\)都是割点。
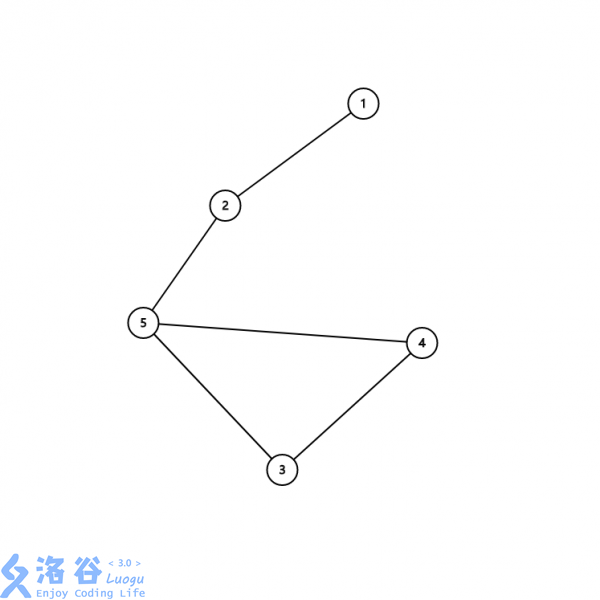
在这里我们还是用到了\(dfn\)数组和\(low\)数组。
现在我们来看第一种情况,大家都知道如果\(dfn_i = 0\)代表\(i\)节点没有被访问过。
那么访问根节点的所有出边,如果发现\(dfn_i = 0\)的次数\(≥ 2\),就满足了第一种情况。
但是如果根节点的两条出边构成了一个环怎么判断?
这就不用担心了,由于是dfs,即时构成了环,我们在访问其中一条出边的时候,就会dfs下去,把另外一条出边也访问过啦,等回溯到根节点的时候,另外一条出边是不会再算一遍的。
接下来就是第二种情况了。
假设现在正在访问\(x\)的出边,同样有两种情况,一种是访问到\(x\)的子节点,另一种是访问到\(x\)的父亲。
如果是访问到\(x\)的父亲,\(low_x = min(low_x, dfn_{fa})\)。
如果是访问到\(x\)的子节点,\(low_x = min(low_x, low_y)\),同时当\(low_y ≥ dfn_x\)时,确定\(x\)是割点,因为\(x\)的上下两部分无法连成环。
核心部分代码:
void tarjan (int x, int fa) { //fa记录的是着整个强联通分量的根节点
int child = 0;
dfn[x] = ++ cnt;
low[x] = cnt;
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) { //这边只有在x有子节点时才会执行,因此省略了x是叶子节点时的情况
tarjan(y, fa);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x] && x != fa) //第二种情况不考虑x是根节点时
cut[x] = 1; //标记x为割点
if (x == fa) //x是根节点时记录他的子节点数量
child ++;
}
low[x] = min(low[x], dfn[y]);
}
if (child >= 2)
cut[x] = 1;
if (cut[x])
ans ++; //计算割点数量
}
之后还是模板题
代码:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 20010, M = 100010;
int n, m, head[N], ver[M << 1], Next[M << 1], tot, dfn[N], low[N], cnt, ans, cut[N];
inline void add (int x, int y) {
ver[++ tot] = y;
Next[tot] = head[x];
head[x] = tot;
}
void tarjan (int x, int fa) {
int child = 0;
dfn[x] = ++ cnt;
low[x] = cnt;
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y, fa);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x] && x != fa)
cut[x] = 1;
if (x == fa)
child ++;
}
low[x] = min(low[x], dfn[y]);
}
if (child >= 2)
cut[x] = 1;
if (cut[x])
ans ++;
}
int main () {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i ++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
for (int i = 1; i <= n; i ++)
if (!dfn[i])
tarjan(i, i);
printf("%d\n", ans);
for (int i = 1; i <= n; i ++)
if (cut[i])
printf("%d ", i);
return 0;
}
Tarjan求边双
void tarjan (int x, int fa) {
dfn[x] = ++ cnt;
low[x] = cnt;
for (int i = head[x]; i; i = nex[i]) {
int y = ver[i];
if (y == fa) continue;
if (!dfn[y]) {
tarjan(y, x);
low[x] = min(low[x], low[y]);
} else low[x] = min(low[x], dfn[y]);
if (low[y] <= dfn[x])
cut[id[i]] = 1;
}
}
试题
题解
受欢迎的牛
题意十分简单。
先思考这题的思路:如果某个节点的出度为\(0\),而其他节点的出度都不为\(0\),那么显然这个节点就是符合要求的节点(即受欢迎的牛);但是如果有两个节点的出度都为\(0\),那么这张图中没有符合要求的节点。
因为如果某只牛的出度不为\(0\),那么它的喜欢就可以一直向它的子节点传递,直到传递到一只出度为\(0\)的牛,因此显然如果图中只有一个节点出度为\(0\),那么它就是受欢迎的牛。
可是这题给出的图中可能会出现强联通分量,很显然一个强联通分量中的牛都是互相喜欢的。
那么我们不妨把每个强联通分量都看成一个节点,即缩点,然后再用上上面所讲的方法,最后求出的出度为\(0\)的缩点所包含的牛的数量即是答案。
代码:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 10010, M = 50010;
int n, m, head[N], nex[M << 1], ver[M << 1], tot, sta[N], vis[N], dfn[N], low[N], cnt, col[N], num[N], deg[N], ans;
inline void add (int x, int y) {
ver[++ tot] = y;
nex[tot] = head[x];
head[x] = tot;
}
void tarjan (int x) {
dfn[x] = low[x] = ++ cnt;
sta[++ sta[0]] = x;
vis[x] = 1;
for (int i = head[x]; i; i = nex[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (vis[y])
low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
int tmp = 1;
vis[x] = 0;
col[x] = ++ col[0];
while (sta[sta[0]] != x) {
col[sta[sta[0]]] = col[0];
vis[sta[sta[0] --]] = 0;
tmp ++;
}
sta[0] --;
num[col[0]] = tmp;
}
}
int main () {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i ++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
}
for (int i = 1; i <= n; i ++)
if (!dfn[i])
tarjan(i);
for (int x = 1; x <= n; x ++)
for (int i = head[x]; i; i = nex[i]) {
int y = ver[i];
if (col[x] != col[y])
deg[col[x]] ++;
}
for (int i = 1; i <= col[0]; i ++)
if (!deg[i]) {
if (!ans)
ans = num[i];
else {
ans = 0;
break;
}
}
printf("%d", ans);
return 0;
}
BLO-Blockade
同样很简单的题意。
把某个节点删掉,求出减少的拜访次数(即多少个有序点对无法到达)。
如果删除的节点不是割点,那么它删除后对答案是没有贡献的,因为剩下的\(n - 1\)个点都能互相到达,那么答案就是原本的次数减去剩下的\(n - 1\)个点产生的次数,即\(ans = n * (n - 1) - (n - 1) * (n - 2)\)。
如果这个节点时割点,那么删除它后,这张图会被分成几个连通块,那么答案就是原本的次数减去每个连通块产生的次数,即\(ans = n * (n - 1) - \sum{k * (k - 1)}\),\(k\)为当前连通块的节点个数。
割点的判断我们已经知道了,现在需要解决的就是删除这个点产生的连通块是怎么样的。
设\(x\)节点时一个割点,它的子节点为\(y\)。
我们知道割点的判定是\(low_y ≥ dfn_x\),其实,如果满足这个条件,\(y\)节点及它的子部分就是删除\(x\)后所产生的其中一个连通块。
同时不要忘了\(x\)的父亲节点以上的部分也是一个连通块。
代码:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 100010, M = 500010;
int n, m, head[N], nex[M << 1], ver[M << 1], tot, dfn[N], cut[N], low[N], size[N], cnt;
long long ans[N];
inline void add (int x, int y) {
ver[++ tot] = y;
nex[tot] = head[x];
head[x] = tot;
}
void tarjan (int x, int fa) {
int child = 0;
long long tmp = 0, s = 0;
dfn[x] = low[x] = ++ cnt;
size[x] = 1;
for (int i = head[x]; i; i = nex[i]) {
int y = ver[i];
if (!dfn[y]) {
tarjan(y, fa);
size[x] += size[y];
low[x] = min(low[x], low[y]);
if (x == fa) {
child ++;
tmp += 1LL * size[y] * (size[y] - 1);
s += size[y];
}
else if (low[y] >= dfn[x]) {
tmp += 1LL * size[y] * (size[y] - 1);
s += size[y];
cut[x] = 1;
}
} else
low[x] = min(low[x], dfn[y]);
}
if (child >= 2)
cut[x] = 1;
ans[x] = 1LL * n * (n - 1);
if (cut[x]) {
ans[x] -= tmp + 1LL * (n - s - 1) * (n - s - 2);
} else
ans[x] -= 1LL * (n - 1) * (n - 2);
}
int main () {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i ++) {
int x, y;
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
tarjan(1, 1);
for (int i = 1; i <= n; i ++)
printf("%lld\n", ans[i]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号