Tarjan求LCA

什么是LCA

LCA即是树上两个节点的最近公共祖先。

这个应该都知道是什么意思吧= =

Tarjan求LCA

这个一个离线算法（离线算法就是把所有询问先读入并储存，最后再把答案一起输出），它的算法流程如下：

当访问到某个节点，且还未回溯到这个节点时，把这个节点标记为\(1\)。

如果已经访问并回溯到了某个节点，把这个节点标记为\(2\)。

假设我们访问到了\(x\)节点，此时\(x\)的某个子节点\(y\)已经回溯，那么\(fa_y = x\)。

按照上面说的这么做，假设现在刚回溯到\(x\)，我们想知道\(x\)与\(y\)的最近公共祖先（\(y\)节点已经被标记为\(2\)），我们会惊奇地发现，它们的最近公共祖先就是\(y\)节点的祖先中第一个标记为\(1\)的节点。

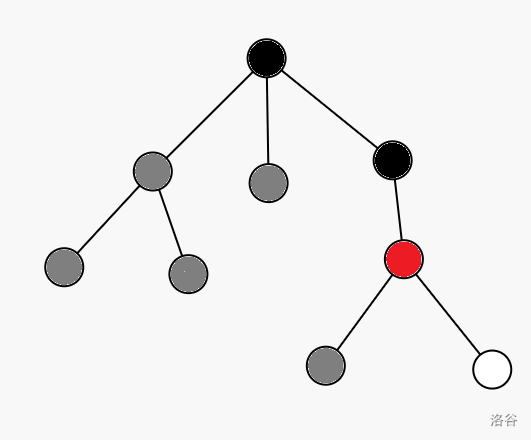
上面这张图中，黑色节点表示标记为\(1\)的节点，灰色节点表示标记为\(2\)的节点，红色节点表示我们现在刚回溯到的节点，此时这个红色节点先看做是黑色节点。

那么此时图中的灰色节点的第一个黑色祖先即是与红色节点的最近公共祖先。

最后用并查集优化就可以快速找到灰色节点的第一个黑色节点祖先了qwq

时间复杂度\(O(n + m)\)，应该比倍增求LCA快！

代码：

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int N = 500010;
int n, m, s, head[N], nex[N << 1], ver[N << 1], tot, ans[N], vis[N], fa[N], headQue[N], nexQue[N << 1], verQue[N << 1], valQue[N << 1], cnt;
inline int read () {
	int res = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		res = (res << 3) + (res << 1) + (ch - 48);
		ch = getchar();
	}
	return res;
}
inline void add (int x, int y) {
	ver[++ tot] = y;
	nex[tot] = head[x];
	head[x] = tot;
}
inline void addQue (int x, int y, int z) {
	verQue[++ cnt] = y;
	valQue[cnt] = z;
	nexQue[cnt] = headQue[x];
	headQue[x] = cnt;
}
int get (int x) {
	if (x == fa[x]) return x;
	else return fa[x] = get(fa[x]);
}
void tarjan (int x) {
	vis[x] = 1; //刚访问到这个节点，标记为1 
	for (int i = head[x]; i; i = nex[i]) {
		int y = ver[i];
		if (vis[y]) continue;
		tarjan(y);
		fa[get(y)] = get(x); //此时y是x的子节点并且已经回溯，那么把y的父亲节点设为x，这里用到了并查集的合并操作 
	}
	for (int i = headQue[x]; i; i = nexQue[i]) {
		int y = verQue[i], id = valQue[i];
		if (vis[y] == 2) //标记为2即图中的灰色节点 
			ans[id] = get(y); //y的祖先就是x和y的最近公共祖先 
	}
	vis[x] = 2;
}
int main () {
	n = read();
	m = read();
	s = read();
	for (int i = 1; i <= n; i ++)
		fa[i] = i;
	for (int i = 1; i < n; i ++) {
		int x = read(), y = read();
		add(x, y);
		add(y, x);
	}
	for (int i = 1; i <= m; i ++) {
		int x = read(), y = read(); //用邻接表储存读入的数据 
		addQue(x, y, i);
		addQue(y, x, i);
	}
	tarjan(s);
	for (int i = 1; i <= m; i ++)
		printf("%d\n", ans[i]);
	return 0;
}

做做模板题吧！