数字电路 - 卡诺图的应用型解释
本文以浅显详细的语言就如何掌握卡诺图的应用提出一种学习思路。
卡诺图(K-map)是一种用于快速化简布尔代数的图形方法,在它对应的布尔函数中有 n 个变量的情况下,它便有 2^n 个格子。本文讨论 3 变量与 4 变量的情况,以 A B C D 指代变量。
3 变量卡诺图中,把相邻的 2 个变量分为一组作为首行,剩下的 1 个分为一组作为首列(也可以交换),在表格中分别填入对应变量的布尔值,并遵循相邻原则,相邻格子所表示的布尔值每次只变化一位,最终:
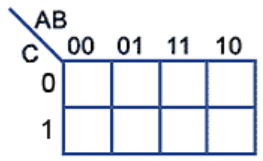
AB 行的布尔值两位分别代表 A 和 B 的值,顺序有意义。
4 变量卡诺图中,将变量两两分组,同样:
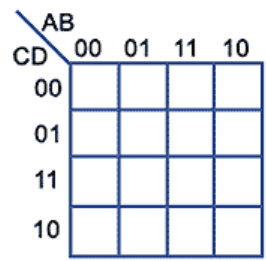
在应用中,需要绘制的布尔函数有两种可能的方式来表示:
1. 使用真值表时:
3 变量真值表(Value Table)形如:
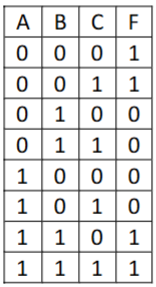
相应地将 F 的值为 1 的位置填入绘制的卡诺图中:
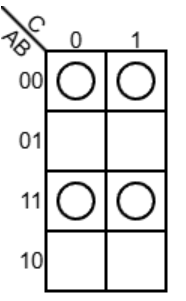
也就是“ABC都为0”“AB为0,C为1”“AB为1,C为0”“ABC都为1”这四个格子。
将有值的格子视为“1”,接下来【圈起】所有的“1”,并遵循以下原则:
- 圈起的“1”的个数必须为2^n个,即2,4,8,16,32... 但圈圈的个数不限
- 圈出范围内可能的最大圈,否则得出的将不是最简布尔式(但仍可接着化简)
- 尽量圈住所有的“1”
- 表格边界的格子可以跨表视作相邻,即最上行和最下行,最左列和最右列的格子
对于本例,圈出的是:
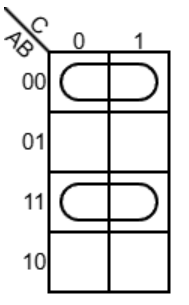
解读的方法为 圈内同写异不写,也就是对于圈住的格子,如果某个变量在每一个格子对应的布尔值都是相同的 0 或 1,就以 0 -> 该变量'(反);1 -> 该变量 的规则记为【写】,否则忽略。
将【写】的变量的布尔值运用布尔代数,以交集的方式(相乘)联合,再以并集的方式(相加)将各个圈圈的结果联合:
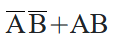
得出的这个式子即为该布尔表达式的最简式。
熟悉了最基本的方法后,本文讲解另一个更复杂的例子,并介绍 4 变量卡诺图以及无关项的解读。
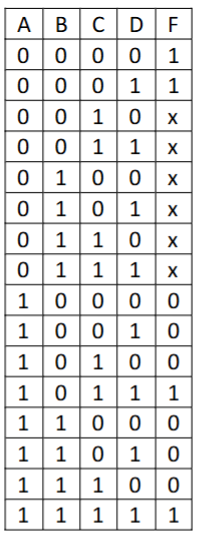
这个真值表中,F 列有的格子值为x,即表示这个格子的值为无关项,无论是 0 或 1,都不会影响最终将要得出的式子,因此在卡诺图的解读中,看怎样更方便我们画圈圈,把这些无关项视作对我们便利的任意值。
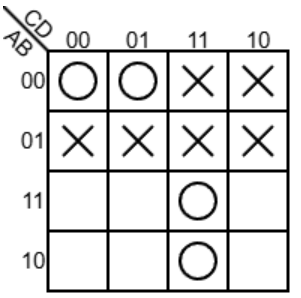
对于这个例子,我们会发现它们全为 1 更好,所以最终:
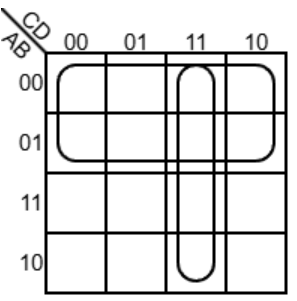
(注意即使圈圈有相交的部分,也不影响我们将它们各自视为完整的圈圈解读)
得出的式子:
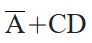
为了更好地说明这条画圈圈的规则

请看另一个例子。对于这个卡诺图:
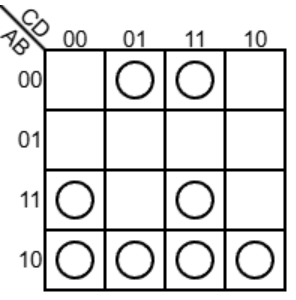
首先最容易圈出来的是:
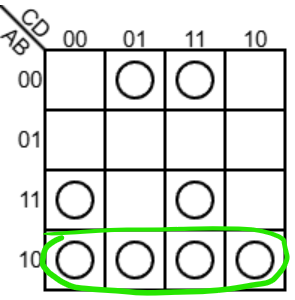
接着圈出另外两个:
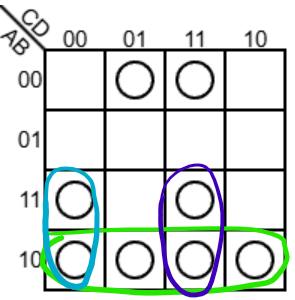
但最后我们需要考虑到这条规则,将这四个格子视为相邻并圈出:
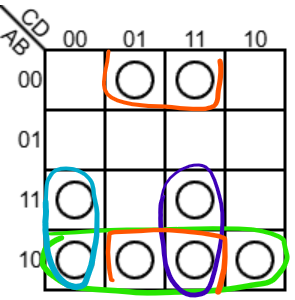
最终即是:
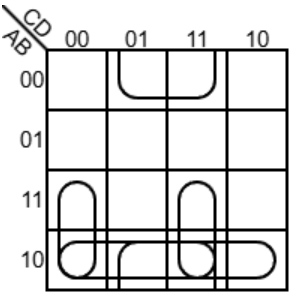
得出的式子:
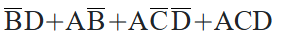
2. 使用代数方式时:
对于 3 变量与 4 变量,解读方式不同。我们先记住这两套换算:
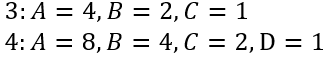
以这个式子为例 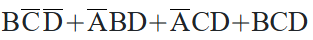
对于每一个出现在加号之间的乘积项,当其中包含值为 1 的变量(出现了而且上面没有杠)时,将这个变量对应上面的换算,如果有多个就相加,在每个乘积项之中各自得出结果,并对应到下图中:

(这个图理解为由真值表对应的变量布尔值所组成的二进制数转换为十进制数得出,0000 -> m0,0001 -> m1,0011 -> m3,0010 -> m2)
式子中的数字对应的位置便是我们将绘制的卡诺图中需要标为“1”的格子。
解读方式与前面提过的一样是画圈圈。
对于 3 变量的卡诺图:

有时需要化简的式子会以这种形式提出:
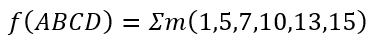
这种式子相当于已经算出了每个乘积项的结果,以同样的方式对应即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号